Задачи тестов

1.Если c_p=1,2,R=200 , тоc_v в Дж/(кг·К) равна 1000.

2.Если с_v = 1 , к=1,5, то газовая постоянная рабочего тела, равна __ кДж/(кг·К).

3.Рабочим телом является аргон. Его показатель адиабаты при t = 0°C в идеально-газовом состоянии равен 1,66.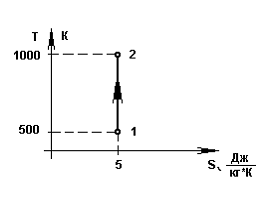

4.Рабочим телом процесса 1 – 2, показанного на рисунке, являются аргон, окись углерода, двуокись углерода и пары этилового спирта. Показатель адиабаты k=1,4 соответствует окиси углерода.

12.Количество теплоты в процессе 1 – 2, показанном на графике, определяется по формуле q=c_cp.

2. Первый закон термодинамики

2.1. Термодинамическая система и параметры её состояния

Термодинамическое состояние однофазного тела можно однозначно определить 3-мя параметрами – удельным объемом (v), температурой (Т), давлением (р).

Они связаны между собой уравнением состояния f(p,v,T) = 0.

Равновесным состоянием называется состояние тела, при котором во всех его точках объема Р, v, Т и все другие физические свойства одинаковы.

Совокупность изменений состояния термодинамической системы при переходе из одного состояния в другое называется термодинамическим процессом.

Если при любом термодинамическом процессе изменение параметра состояния не зависит от вида процесса, а определяется начальным и конечным состоянием, то параметры состояния называются функцией состояния. Такими параметрами являются внутренняя энергия, энтальпия, энтропия.

2.2. Внутренняя энергия

Внутренней энергией (U) для идеальных газов называют кинетическую энергию движения молекул. Отнесённая к 1 кг газа, она называется удельной внутренней энергией и обозначается u (Дж/кг).

По молекулярно-кинетической теории внутренняя энергия идеального газа равна:

u= с_v Т.

Видим, что внутренняя энергия зависит только от температуры и поэтому является функцией состояния газа. Изменение внутренней энергии при переходе из одного состояния в другое всегда равно разности между ее значениями в конечном и начальном состояниях независимо от пути, по которому совершался переход:

∆u= с_v (Т₂-Т₁). (2.1)

2.3. Теплота и работа

Внутренняя энергия рабочего тела изменяется в термодинамическом процессе при передаче энергии другому телу, которая может происходить двумя способами: в форме теплоты и в форме работы.

В форме теплоты. Реализуется при непосредственном контакте тел, имеющих различную температуру, путем обмена кинетической энергией между молекулами соприкасающихся тел либо лучистым переносом внутренней энергии излучающих тел путем электромагнитных волн. При этом энергия передается от более нагретого к менее нагретому.

Количество энергии, переданной в форме теплоты от одного тела к другому, называется количеством теплоты – Q [Дж],

1 Дж = 1 Нм.

Подведенная теплота считается положительной, отведенная - отрицательной.

В форме работы. Передача энергии происходит при условии перемещения всего тела или его части в пространстве. При этом количество переданной энергии называется работой – А [Дж].

Количество энергии, полученное телом в форме работы, называется работой, совершенной над телом (отрицательна), а отданную энергию – затраченной телом работой (положительна).

Количество теплоты, полученное (отданное) телом, и работа, совершенная (затраченная) над телом, зависят от пути перехода тела из начального состояния в конечное, т.е. являются функциями процесса.

Работа в термодинамике, как и в механике, определяется произведением действующей на рабочее тело силы на путь ее действия.

Рассмотрим газ, заключенный в цилиндре с подвижным поршнем площадью F. Если газу сообщить некоторое количество теплоты, то он будет расширяться, совершая при этом работу против внешнего давления р, оказываемого на него поршнем.

Газ действует на поршень с силой, равной p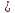F, и совершает элементарную работу δА =pFdy, перемещая поршень на расстояние dy. Но Fdy представляет собой увеличение объема системы, следовательно, δА = pdV.

При конечном изменении объема 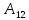= . (2.2)

Работа А против сил внешнего давления, связанная с изменением объема системы, носит название работы деформации.

Поскольку р – величина положительная, δА и dV всегда имеют одинаковые знаки:

На рисунке элементарная работа расширения газа представлена площадью ∆A элементарного прямоугольника высотой р и протяжённостью основания ∆V. Соответственно суммарная работа расширения газа отображается на термодинамическойpV диаграмме площадью, ограниченной сверху графиком процесса расширения, снизу – осью координат, слева и справа – границами расширения.

Величина работы зависит от того, каким путем совершался переход из начального состояния в конечное. На рисунке изображены три различных процесса, переводящих газ из состояния (1) в состояние (2). Во всех трех случаях газ совершает различную работу.

Удельной энтальпией называется величина: h = u+pv . (2.3)

Поскольку U, p и V являются параметрами состояния, то и энтальпия является функцией состояния. Энтальпия представляет собой полную энергию тела - сумму внутренней энергии U и потенциальной энергии давления pV.

∆h= с_p (Т₂-Т₁).

Энтальпия широко используется при расчётах процессов с парами и газами при высоких температурах. Так как в расчётах важно изменение энтальпии, то знания абсолютных значений не требуется. В связи с этим принято H = 0 при t = 0 .

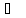Ещё одной функцией состояния является удельная энтропия: ds = . (2.4)

Энтропия есть однозначная функция состояния тела, принимающая для каждого состояния вполне определенное значение и в любом термодинамическом процессе полностью определяется начальным и конечным состоянием тела и не зависит от пути протекания процесса.

Если энтропия системы возрастает (∆s > 0), то системе подводится тепло. Если энтропия системы уменьшается (∆s < 0), то от системы отводится тепло. Если энтропия системы не изменяется (∆s = 0, s = Const), то системе не подводится и не отводится тепло (адиабатный процесс).

Элементарная удельная теплота определяется по формуле: dq = T ds (2.5).

Теплота процесса 1-2 пропорциональна площади под графиком процесса при его изображении в Ts координатах.