
Математика 2 семестр / Математика 2 семестр / Оптимизация функции
.pdfЗадание: ОПТИМИЗАЦИЯ ФУНКЦИИ
Оптимальные значения функции f (x, y) на некотором множестве D ‒ ее наибольшее fнаиб. fMAX и наименьшее fнаим. fMIN значения (заглавные латинские буквы подразумевают "глобальный" максимум и минимум, в отличие от локальных, которые будем обозначать строчными буквами ‒ fmax и fmin ). Оптимальные точки функции ‒ точки, в которых функция принимает
оптимальные значения. Задача оптимизации функции состоит в нахождении ее оптимальных значений и оптимальных точек. Естественно, имеется две задачи оптимизации ‒ поиск наибольшего
значения и поиск наименьшего значения. Решение задачи оптимизации ‒ пара fOPT , ARGOPT
из оптимального значения fOPT и набора ARGOPT оптимальных точек, в которых функция принимает это значение. Если множество D компактно, а функция f непрерывна, то обе задачи оп-
тимизации имеют решение (теорема Вейерштрасса). Если оптимальное значение принимается в единственной точке, то говорят, что решение единственное. Ситуацию, когда оптимальное значение принимается в нескольких точках, называют "альтернативным оптимумом".
Пример 1. Пусть f (x) sin x , D ( ; ) . Тогда fMAX 1, ARGMAX / 2 2 k, k Z , fMIN 1, ARGMIN / 2 2 k, k Z .
Пример 2. Пусть f (x) sin x , D (0; ) . Тогда fMAX 1, ARGMAX / 2 , наименьшего значения в данном случае нет (почему?).
Домашнее задание состоит из двух частей ‒ исследование критических (в данном случае, стационарных) точек функции в области ее определения и задача оптимизации функции в указанной области.
1. Найти и исследовать критические точки функции f (x, y) ( y 1)2 (x 3) (x 5)2 10.
Решение. Область определения функции ‒ R2 (вся плоскость). Находим точки стационарности функции ‒ точки, в которых grad f (x, y) 0 , точки, в которых все частные производные
равны нулю. Вычисляем f (x, y) ( y 1)2 |
2(x 5) , |
f (x, y) 2( y 1)(x 3) и решаем систему |
x |
|
y |
|
( y 1)2 2(x 5) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнений |
|
. Получаем три стационарных точки (они же ‒ "подозритель- |
||||||||||||||||
|
2( y 1)(x 3) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ные" на локальный экстремум): M1 (3; 3) , M2 (3;1) |
и M3 (5; 1) . |
|
|
|
|
|
||||||||||||
Вычисляем вторые производные и записываем матрицу Гессе: |
f (x, y) 2 , |
f (x, y) 2(x 3) , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xx |
|
|
|
yy |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, y) |
|
(x, y) |
|
|
2 |
2( y 1) |
|
|
f (x, y) |
f |
(x, y) 2( y 1) . Матрица |
H (x, y) |
fxx |
fxy |
|
. |
|||||||||||
|
f |
(x, y) |
f |
(x, y) |
2( y 1) 2(x 3) |
|||||||||||||
xy |
yx |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
yx |
|
yy |
|
|
|
|
|
|
|
Точка M1 (3; 3) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
4 |
|
|
4 |
|
16 |
0 . Согласно признаку, в точке M1 (3; 3) |
|
||||||||||
2 |
|
|
||||||||||||||||
H (M1 ) |
4 |
, Det H (M1 ) |
4 |
0 |
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
локального экстремума нет (седловая точка, точка гиперболического типа).
Точка M2 (3;1) : |
|
|
|
|
|
|
|
|||
H (M2 ) |
2 |
4 |
|
2 ) |
|
4 |
|
16 |
0 . Согласно признаку, в точке M2 (3;1) |
локально- |
2 |
|
|||||||||
|
|
, Det H (M |
|
|
|
|||||
|
4 |
0 |
|
|
4 |
0 |
|
|
|
|
го экстремума нет (седловая точка, точка гиперболического типа).
Точка M3 (5; 1) : |
|
|
|
|
|
|
|
|
|
||
2 |
0 |
|
Det H (M3 ) |
|
0 |
|
8 |
0 . Согласно признаку, в точке M3 (5; 1) |
|
||
2 |
|
|
|||||||||
H (M3 ) |
4 |
, |
0 |
4 |
|
есть ло- |
|||||
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
(M3 ) 2 |
0 , то M3 (5; 1) ‒ точка |
|
кальный экстремум (точка эллиптического типа). Так как fxx |
|||||||||||
локального минимума. Значение f (M3 ) f (5; 1) 10 .
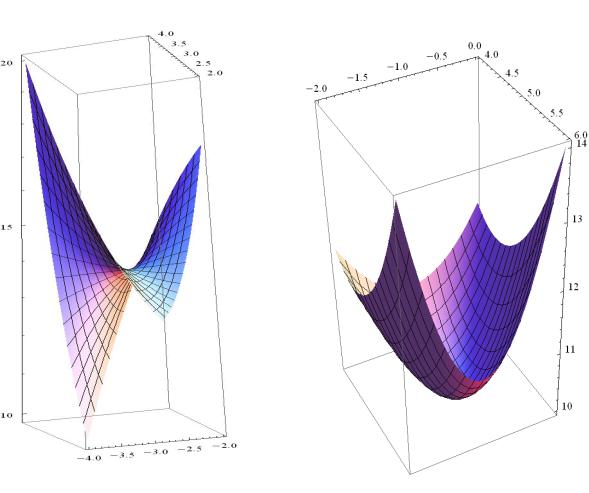
График в окрестности седловой точки |
График в окрестности точки локального минимума |

2. Найти наибольшее fMAX и наименьшее fMIN значения этой функции в области D , ограниченной линиями y x , y 2 , x 1 и x 6 .
Рисуем область.
|
y |
|
|
C |
M4 |
y 2 |
B |
E |
M6 |
M2 |
|
x 1 |
O |
|
x |
|
|
|
|
|
|
M3 |
M5 |
|
|
|
|
|
|
M1 |
x 6 |
|
|
|
|
|
|
y x |
|
|
6 |
|
A |
|
|
|
Получился четырехугольник (трапеция) ABCE .
Из общих соображений понятно, что оптимальные точки следует искать среди точек локальных экстремумов, лежащих внутри области, и среди точек на границе области. Маленькая хитрость состоит в том, что в задаче оптимизации, как правило, не проводят исследование критических точек на экстремум, ограничиваясь только вычислением значений функции.
Из первой части задания выписываем критические точки, попавшие вовнутрь области, и вычисляем значения функции: M2 (3;1) , f (M2 ) 14 ; M3 (5; 1) , f (M3 ) 10 .
Приступаем к исследованию функции на границе области (так называемая задача условной оптимизации ‒ найти оптимальные значения функции при условии, что ее аргумент находится на границе области). Граница состоит из четырех отрезков, поэтому придется четыре раза проделать примерно одно и то же.
Отрезок CB . Его уравнение y 2 , 1 x 6 . Обозначим fCB (x) функцию |
f (x, y) при усло- |
||||
вии, что y 2 . В данном случае f |
CB |
(x) f (x; 2) 9(x 3) (x 5)2 10 |
x2 x 8 . Получаем |
||
|
|
|
|
|
|
"школьную" задачу ‒ найти наибольшее и наименьшее значение функции |
f |
CB |
(x) x2 x 8 на |
||
отрезке [ 1; 6] .
Вычисляем производную, приравниваем ее к нулю, находим критические точки, попавшие вовнутрь отрезка, затем вычисляем значения функции в этих точках и на концах промежутка.
|
(x) 2x 1 0 |
x 0,5[1; 6] ; |
fCB 0,5 7, 75, |
fCB 1 10 , |
fCB 6 38 . |
fCB |
Возвращаемся к исследуемой функции. Вспоминаем, что на отрезке CB y 2 . В области определения возникает новая точка M4 (0,5; 2) (отмечаем ее на рисунке) и f (M4 ) fCB (0,5) 7, 75 . Концы отрезка ‒ точки C и B , поэтому f (C) fCB (1) 10 , f (B) fCB (6) 38 .
Отрезок AB . Его уравнение x 6 , 6 y 2 . Обозначим |
fAB ( y) функцию f (x, y) при усло- |
|||||
вии, что x 6 . В данном случае f |
AB |
( y) f (6; y) 3( y 1)2 |
11. Получаем задачу ‒ найти |
|||
|
|
|
|
|
|
|
наибольшее и наименьшее значение функции f |
AB |
( y) 3( y 1)2 11 на отрезке [ 6; 2] . |
||||
|
|
|
|
|
|
|
|
y 1[6; 2] ; fAB |
1 11, fAB 6 86 , fAB 2 38 . |
||||
fAB ( y) 6( y 1) 0 |
||||||
Последнее значение можно было не вычислять (почему?). Разве что для контроля вычислений.
Возвращаемся к исследуемой функции. На отрезке AB x 6 . В области определения возникает новая точка M5 (6; 1) и f (M5 ) fAB (1) 11. На конце A имеем f (A) fAB (6) 86 .
Отрезок CE . Его уравнение x 1 , 1 y 2 . Обозначим fCE ( y) функцию f (x, y) при условии,
что x 1. В данном случае f |
CE |
( y) f ( 1; y) 4( y 1)2 46 . Получаем задачу ‒ найти |
|||
наибольшее и наименьшее значение функции f |
CE |
( y) 4( y 1)2 |
46 на отрезке [1; 2] . |
||
|
|
|
|
|
|
f ( y) 8( y 1) 0 y 1[1; 2], остается только вычислить значение функции на левом
CE
конце: fCE 1 20 .
Возвращаемся к исследуемой функции. На отрезке CE x 1 , поэтому f (E) fCE (1) 20 .
Остался отрезок EA . Его уравнение y x , |
1 x 6 . Обозначим fEA (x) функцию f (x, y) |
||||||||||||||
при условии, что y x . В данном случае |
|
|
|
||||||||||||
f |
EA |
(x) f (x; x) ( x 1)2 (x 3) (x 5)2 |
10 x3 4x2 3x 32 . Ищем наибольшее и |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наименьшее значение функции |
|
|
f |
EA |
(x) x3 |
4x2 |
3x 32 на отрезке [ 1; 6] . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
(x) 3x2 8x 3 0 |
x |
|
1 |
[ 1; 6], |
x 3 [ 1; 6] . Очень редкое явление ‒ "хоро- |
||||||||
|
|||||||||||||||
|
EA |
|
|
|
|
1 |
|
|
3 |
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
878 |
|
|
|
fEA 3 14 . Значения на концах можно не вычислять. |
||||||
шие корни". Далее fEA |
|
|
|
|
|
|
|
32,5 , |
|||||||
|
|
|
|
|
|||||||||||
|
|
|
3 |
|
|
|
27 |
|
|
|
|
|
|
||
Возвращаемся к исследуемой функции. Уравнение отрезка EA |
y x . В области определения |
возникает новая точка M6 (1/ 3;1/ 3) и уже знакомая по из первой части точка M1 (3; 3) . По- |
|
следние вычисления: f (M6 ) fEA (1/ 3) 878 / 27 32,5 , а |
f (M1) fEA (3) 14 . |
Осталось "подведение итогов". Выписываем все отмеченные точки и значения функции в этих точках в таблицу (не обязательно):

f (M1) f (3; 3) 14 |
|
|
|
f (M2 ) f (3;1) 14 |
|
|
|
f (M3 ) f (5; 1) 10 |
|
|
|
f (M4 ) f (0,5; 2) 7, 75 |
MIN |
|
|
f (M5 ) f (6; 1) 11 |
|
f (M6 ) f ( 1/ 3;1/ 3) 32,5 |
|
f (A) f (6; 6) 86 |
MAX |
|
|
f (B) f (6; 2) 38 |
|
|
|
f (C) f ( 1; 2) 10 |
|
|
|
f (E) f ( 1;1) 20 |
|
|
|
Остается записать ответ и посмотреть на картинку.

Дополнение. Множество точек, в которых определитель матрицы Гессе равняется нулю (точек па- |
|||||
раболического типа) оказывается параболой, определяемой уравнением |
|
||||
1 DetH (x, y) |
1 |
2 |
2( y 1) x 3 ( y 1)2 0 . |
|
|
4 |
4 2( y 1) |
2(x 3) |
|
|
|
Парабола разбивает плоскость на две области |
|
|
|
||
2 |
|
|
|
|
|
5 |
|
10 |
15 |
20 |
25 |
2 |
|
|
|
|
|
4 |
|
|
|
|
|
Все точки вне параболы имеют гиперболический тип, а внутри ‒ эллиптический тип. Во внутрен- |
|||||
ней области функция выпукла вниз, а все точки графика, расположенные над внешней областью ‒ |
|||||
седловые. |
|
|
|
|
|
На поверхности графика лежит прямая линия, проходящая через точку (3; 0;14) , параллельная оси Oy . Ее можно разглядеть на втором рисунке.
