
ДМ лекции
.PDF8 . РЕЗБОВЫЕ СОЕДИНЕНИЯ
Резьбовые соединения являются одними из старейших и наиболее распространенных видов разъемных соединений (до 60% деталей в машине содержат резьбу). К ним относятся соединения с помощью болтов, винтов, винтовых стяжек, резьбы на валах, резьбовые отверстия в корпусных деталях и т.п.
Достоинства и недостатки болтовых соединений
Достоинства:
1)простота сборки и разборки соединения;
2)малые габариты (при этом можно обеспечить большие усилия затяжки);
3)наличие широкой номенклатуры стандартных резьбовых изделий;
4)высокая экономичность.
Основной недостаток – резьба – концентратор напряжения на поверхности детали.
Методы изготовления
1)вручную метчиком, плашкой;
2)на токарно-винторезном станке;
3)на резьбофрезерных станках (резьбы большого диаметра);
4)накатка;
5)литьем (стекло, пластмассы);
6)выдавливание (тонколистовые резьбовые детали).
Классификация резьбовых соединений
I.По форме поверхности, на которой образована резьба:
1)цилиндрические;
2)конические.
II. По форме профиля резьбы: 1) треугольная:
151

-метрическая (основная крепежная резьба) с треугольным профилем
(рис. 8.1 а); - треугольная со скругленными вершинами и впадинами (трубная –
крепежно-уплотнительная резьба) (рис. 8.1 б);
2)трапецеидальные резьбы (ходовые):
-трапецеидальная симметричная (рис. 8.1 в);
-трапецеидальная не симметричная (достоинство: потери на трение при движении различные (рис. 8.1 г);
3)прямоугольная (частный случай трапецеидальной; достоинство: самый высокий КПД) (рис. 8.1 д);
d
2 d
p
30
в)
|
|
|
60 |
|
|
|
|
|
|
p |
p |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h= |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
а) |
|
d |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
p0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
h= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
p |
|
3 |
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г)
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||||||||
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
||||||
|
|
|
|
|
|
б) |
|
|
|||||||||||||
57p=0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|||||
h |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
d |
|
|
|
|
|
|
|
|
||||||||||
д)
d
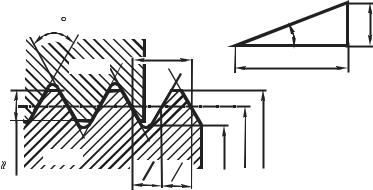
Рис. 8.1. Виды резьб. а – метрическая; б – треугольная со скругленными вершинами и впадинами; в – трапецеидальная симметричная; г – трапецеидальная не симметричная; д – прямоугольная
4) круглая резьба (удобна для выдавливания, для тонкостенных деталей, хорошо работает в загрязненной среде).
III.По направлению винтовой линии:
1)правая (слева направо и вверх) – наиболее распространена;
2)левая (справа налево и вверх) – специальная.
152
IV. По назначению:
1)крепежная (метрическая, трубная, круглая);
2)крепежно-уплотнительная (треугольная со скругленными вершинами
ивпадинами);
3)ходовая (все виды трапецеидальных резьб, в том числе прямоуголь-
ная).
Приведенная классификация не является строгой, т.к. на практике встре-
чаются случаи применения метрической резьбы с мелким шагом в точных измерительных механизмах.
Основные геометрические параметры резьбы
На рисунке 8.2 изображена метрическая резьба: d – наружный диаметр;
d1 – внутренний диаметр.
Номинальные значения d и d1 одинаковы для винта и гайки, а зазоры во впадинах образуются за счет предельных отклонений размеров диаметров.
p 4 0,5
h
60
p
Гайка
Винт |
p 2 |
p 2 |
|
а)
1
d
2 d
d
π
ψ
d2
p1
б)
Рис. 8. 2. Геометрические параметры резьбы. d – наружный диаметр; d1 – внутренний диаметр; d2 – средний диаметр; h – рабочая высота профиля; p – шаг резьбы; p1 – ход резьбы; α – угол профиля; ψ – угол подъема резьбы
153
d2 – средний диаметр (диаметр воображаемого цилиндра, образующая которого пересекает резьбу в таком месте, где ширина выступа (витка) равна ширине впадины);
h – рабочая высота профиля, по которой соприкасаются боковые стороны резьб винта и гайки;
p – шаг резьбы (расстояние между одноименными сторонами соседних профилей);
p1 – ход (поступательное перемещение образующего профиля за один оборот или относительное перемещение гайки за один оборот): для однозаходной резьбы p1 = p, для многозаходной p1 = n×p, где n – число заходов;
α – угол профиля, в метрической резьбе α = 60°; ψ – угол подъема (угол подъема развертки винтовой линии по среднему диаметру)
tgψ = |
p1 |
= |
np |
|
|
|
|
. |
(8.1) |
||
πd 2 |
πd 2 |
||||
Все геометрические параметры резьб и допуски на их размеры стандар-
тизованы.
Обоснование преимуществ треугольной резьбы перед прямоугольной при использовании ее в качестве крепежной
Выбор профиля резьбы определяется многими факторами, важнейшие из которых прочность, технологичность и сила трения в резьбе. Так, например,
крепежная резьба должна обладать высокой прочностью и относительно большими силами трения, предохраняющими крепежные детали от самоотвинчивания, а также быть технологичной в изготовлении. Резьбы винтовых механизмов, напротив, должны быть с малыми силами трения, чтобы повысить КПД и уменьшить износ; прочность для них во многих случаях не является основным критерием, определяющим размер винтовой пары.
154
Основной тип крепежной резьбы – это треугольная резьба. Рассмотрим ее преимущества по сравнению с резьбой прямоугольного профиля.
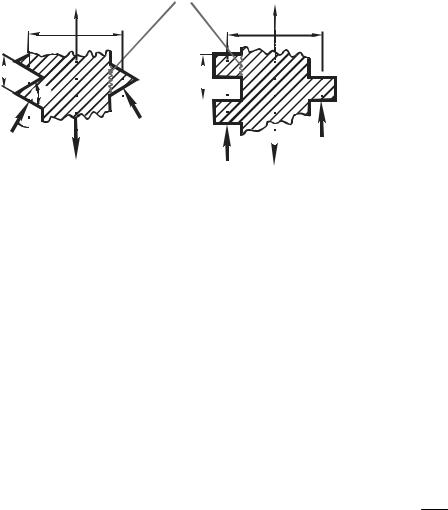
Сравнение выполним, рассматривая нагружение одного витка каждой из резьб (рис. 8.3). Внешняя сила F уравновешивается нормальными силами (Nтр и Nпр) на соответствующих поверхностях витков. Из условия равновесия одного витка треугольной резьбы (сумма всех сил, направленных вдоль оси Y
равна нулю) 2 |
N тр |
a |
= F , откуда N тр = |
F |
; |
|
cos |
|
|||
|
cos a |
||||
2 |
2 |
|
|
||
|
|
|
|
2 |
|
|
Линия разрушения |
|
резьбы от среза |
y |
y |
d |
d |
2 |
2 |
|
тр |
|
|
|
|
|
|
пр |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Nтр |
|
α |
|
|
Nтр |
p |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
Nпр |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 α |
|
|
|
|
|
|
|||||||||
|
|
|
|
F |
Nпр |
|
2 |
|||||||||
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
F |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
а) |
|
|
|
|
б) |
|||||
Рис. 8.3. Схема нагружения силой F одного витка треугольной (а) и прямоугольной (б) резьбы
Сила трения в треугольной резьбе
F f |
|
= N тр × f = F |
f |
= F × f ¢ , |
(8.2) |
|||
тр |
cos a |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
где f |
и× f ¢ = |
f |
– соответственно действительный и приведенный коэффи- |
|||||
|
|
|||||||
a |
||||||||
|
|
|
|
|
|
|||
|
|
|
cos |
|
|
|
||
|
|
|
2 |
|
|
|
|
|
циенты трения.
Аналогично для прямоугольной резьбы получим 2 N пр = F , откуда Nпр = F ,
2
а сила трения в прямоугольной резьбе
F f |
пр |
= N пр × f = F × f . |
(8.3) |
|
|
|
|
|
|
|
155 |
Отношение сил трения в треугольной и прямоугольной резьбах при стан-
дартном угле профиля резьбы , α = 60°
F f тр |
|
1 |
1 |
|
|
|||
|
|
= |
|
|
= |
|
= 1,15 . |
(8. 4) |
F |
f пр |
cos |
α |
cos 30° |
||||
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Из формулы (7.38) следует, что трение в треугольной резьбе на 15% выше, чем в прямоугольной. Это значит, что треугольная резьба обладает меньшей склонностью к самоотвинчиванию. Кроме того, при одинаковых шагах) резьбы pтр = pпр, треугольная резьба имеет большую прочность на срез (а, поскольку резьба, как правило, изготавливается равнопрочной, то и на другие виды разрушения) приблизительно в 2 раза выше, чем прямоугольная (см. ф. 7.49). Отметим, также, что треугольная резьба более технологична, и может изготовляться накаткой, а не только нарезанием.
ТЕОРИЯ ВИНТОВОЙ ПАРЫ
Зависимость между моментом завинчивания и осевой силой
Если винт нагружен осевой силой F, то для завинчивания гайки к ключу необходимо приложить момент завинчивания Тзав, а к стрежню винта – реактивный момент, который удерживает стержень от вращения, при этом можно записать
Tзав = Tр + Tт , |
(8.5) |
где Тт – момент силы трения на опорном торце гайки, Тр – момент силы трения в резьбе.
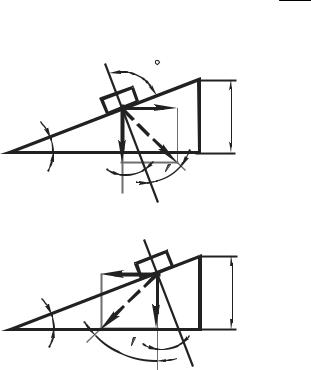
Момент силы трения в резьбе определим, рассматривая гайку как ползун, поднимающийся по виткам резьбы, как по наклонной плоскости
(рис. 8.4. а).
По известной теореме механики, учитывающей силы трения, ползун (гайка) находится в равновесии, если равнодействующая Fn системы внешних сил отклонена от нормали n – n на угол трения φ.
156
|
В нашем случае внешними являются осевая сила F и окружная сила |
||||
F = |
|
2Tр |
. При завинчивании как видно из рис. 8.4, а получим |
||
|
|
||||
t |
|
|
d 2 |
|
|
|
|
|
|
|
|
|
Ft = F × tg(y + j′) , |
||||
или |
(8.6) |
||||
T = |
F × d 2 |
tg(y + j¢), |
|||
|
|||||
р |
2 |
|
|
||
|
|
|
|||
где d2 – |
средний диаметр резьбы, ψ – угол подъема винтовой линии, φ′ – при- |
||||
веденный угол трения j¢ = arctg f ¢ = arctg f .
cos a
|
n |
90 |
|
а |
|
|
|
|
F |
|
|
|
|
1 |
|
|
|
t |
|
|
|
F |
p |
ψ |
F |
|
|
n |
|
||
|
|
|
|
|
ψ |
ϕ |
|
|
|
|
|
|
|
n |
|
б |
F |
n |
|
|
|
||
ψ |
t |
|
|
|
|
1 |
|
|
|
|
p |
F |
|
F |
|
n |
|
|
|
|
ϕ |
ψ |
n |
|
|
|
Рис. 8.4. Схемя поясняющая определение момента трения в резьбе Тр при завинчивании (а) и
отвинчивании (б)
Момент отвинчивания
При отвинчивании (рис. 8.4 б) окружная сила Ft и сила трения Fтр меняют направление.
При этом получим Ft = F tg(j′ - y) . Момент отвинчивания
T = |
Fd 2 |
tg(j¢ - y) . |
(8.7) |
отв
2
Условие самоторможения можно записать в виде Tотв > 0 .
157
Если рассматривать самоторможение только в резьбе без учета трения на торце гайки, получим
T |
Fd |
2 |
tg(ϕ′ − ψ) > 0 , т.е. для самоторможения необходимо чтобы ϕ′ > ψ . |
2 |
|
||
отв |
|
|
Для крепежных резьб ψ ≈ 2°30′, а такому же приведенному углу трения ϕ′
соответствует коэффициент трения f ≈ 0,045.
Реальный коэффициент трения в резьбе при использовании стальных бол-
та и гайки f ≈ 0,1 … 0,15, то есть условие самоторможения надежно выполняется. Но это справедливо при статически приложенных внешних нагрузках.
При переменных нагрузках и особенно при вибрациях вследствие взаимных микросмещений поверхностей трения и коэффициент трения существенно снижается (до 0,02 и ниже). Условие самоторможения нарушается и происходит самоотвинчивание. В связи с этим в таких условиях применяют дополнительные детали, предотвращающие самоотвинчивание (пружинные или отжимные шайбы, шплинты, контргайки, специальные гайки со вставкой из пластмассы и др. [???]).
Существует два пути определения момента сил трения на торце гайки (Тт):
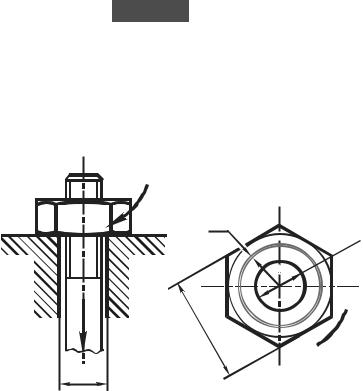
1. Определение уточненного значения момента сил трения на торце
гайки (рис. 8.5)
 F
F
dотв
Tзав |
dρ |
|
|
|
в |
|
|
|
|
|
|
|
т |
|
о |
|
|
d |
|
|
ρ
D
1
 Tзав
Tзав
Рис. 8.5. Схема к определению уточненного значения момента трения на торце гайки
158

Принимая естественное допущение о том, что давление q на кольцевой площадке контакта гайки с поверхностью детали распределяется равномерно, получим
q = |
p (D |
|
F |
|
). |
(8.8) |
|
2 |
- d |
2 |
|||||
|
|
1 |
|
отв |
|
|
|
4 |
|
|
|
||||
|
|
|
|
|
|
||
Рассмотрим элементарную кольцевую площадку на расстоянии ρ от оси гайки и шириной dρ. Тогда элементарная сила трения dF на кольцевой опорной поверхности гайки
d F f = d N × f = q × d A × f = q2p × rd r × f , |
|
|
|
(8.9) |
|
|
|
|||||||||||||
где dN – |
элементарная нормальная сила от давления гайки; dА – элементар- |
|||||||||||||||||||
ная площадь кольца шириной dρ. |
|
|
|
|
|
|
|
|
||||||||||||
Элементарный момент сил трения |
|
|
|
|
|
|
|
|
||||||||||||
d T |
т |
= d F |
× r = q2pf × r2 d r , |
|
|
|
|
|
(8.10) |
|
|
|
||||||||
|
|
|
|
тр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
D |
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
r |
3 |
2 |
3 |
|
3 |
|
||
|
|
2 |
|
|
2 |
|
|
2 |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4F (D1 |
- dотв ) |
|
||||
Tт = d ∫ |
q2pf × r |
|
d r = q2pf d ∫ r |
|
d r = q2pf |
3 |
dотв |
= 2pf |
p × 8 × 3(D |
2 |
- d 2 |
), |
||||||||
|
|
|
отв |
|
|
|
|
|
отв |
|
|
|
|
|
1 |
отв |
|
|||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|||
Окончательно получим |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Ff |
(D3 - d 3 |
|
) |
. |
|
|
|
|
|
(8.11) |
|
|
|
||||
Tт |
= |
|
|
|
1 |
отв |
|
|
|
|
|
|
|
|
|
|||||
3 |
|
(D12 - dотв2 |
) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Определение приближенного значения Тт на торце гайки
Если ширина кольца, по которой проходит трение невелика, то можно воспользоваться приближенным расчетом момента трения на торце Тт. В этом расчете принимается упрощенное допущение о том, что результирующая сил трения приложена на среднем диаметре опорной поверхности гайки (рис. 8.6)
d ср = |
D1 + d отв |
. |
|
|
(8.12) |
||||
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
Тогда момент трения на торце гайки |
|
||||||||
T |
|
= F |
d ср |
= Ff |
d ср |
. |
(8.13) |
||
|
2 |
2 |
|||||||
|
т |
|
тр |
|
|
|
|
||
|
|
|
|
|
|
|
159 |
|
|
Суммарный момент Тзав, который необходимо приложить к гайке для ее равномерного вращения при наличии трения в резьбе Тр и на торце Тт гайки называется моментом завинчивания
T = T |
р |
+ T |
т |
= |
F × d 2 |
tg(y + j¢) + Ff |
|
|
|
||||||
зав |
|
2 |
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tзав
d ср
2
dcр
= |
F × d 2 |
tg(y + j¢) + f |
dср |
. (8.14) |
|
d 2 |
|||
2 |
|
|
||

 Tзав
Tзав
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
т |
||
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 F
F
D
1
 Fтр
Fтр
Рис. 8.6. Схема к определению приближенного значения момента сил трения на торце гайки
Последняя формула (8.14) позволяет оценить отношение осевой силы винта F к силе R, приложенной к ручке гаечного ключа (отношение F/R – выигрыш в силе) (рис 8.7).
Для стандартных метрических резьб можно принять: β = 2°30′; d2 = 0,9d; dср = 1,4d2; для резьб без специальных покрытий коэффициент трения f = 0,15; при этом tg(b + j′) » 0,2 .
При этих условиях получим
T = |
F 0,9d |
(0,2 + 0,15 ×1,4) » 0,2Fd . |
(8.15) |
зав |
2 |
|
160
