
Chernov_-_Vvedenie_v_LP
.pdfТаким образом, если бы удалось увеличить запасы клюквенного сока на 2 л, то бар мог бы получить доход в размере 2040 руб., то есть на 60 руб. больше, чем раньше.
Этот доход он получил бы, изготовив 120 л коктейля "Утро" (на 20 л меньше, чем раньше) и 60 л коктейля "Вечер" (на 30 л больше, чем раньше). Увеличение общего объема продукции на 10 л происходит за счет 2 л недостающего клюквенного сока и 8 л избыточного апельсинового сока. При этом в точке L пересеклись бы все три граничные прямые, так что все запасы соков оказались бы полностью использованными.
Можно сопоставить оптимальный план нашей задачи - точку М с другими вариантами области допустимых планов. Предположим, что бар все имеющиеся запасы соков попытается использовать для изготовления одного лишь коктейля "Утро". Такое решение соответствует точке А на оси Ox1 рис. 7. Бар сумеет выпустить 160 л этого коктейля (вместо 140 л по оптимальному плану), исчерпав при этом все запасы виноградного сока. Остальные ресурсы останутся недоиспользованными. Доход бара будет при этом равен:
12 160 = 1920 (руб.),
на 60 руб. меньше максимально возможного (оптимума).
Можно рассмотреть и другой вариант плана, когда бар все соки использует для изготовления одного лишь коктейля "Вечер". Этот план соответствует точке Е на оси Ox2 рис. 7. Бар выпустит 120 л этого коктейля (вместо 30 л по оптимальному плану), исчерпав полностью запасы апельсинового сока. Запасы остальных соков окажутся недоиспользованными. При этом бар получит доход в размере
10 120 = 1200 (руб.).
что на 780 руб. меньше оптимума.
Недопустимый план F предписывает изготавливать только "Утро" в количестве 176 л. Доход при этом равен
71
12 176 = 2112 (руб.).
Запасы клюквенного сока при таком выпуске исчерпываются полностью. Апельсиновый сок расходуется лишь частично, 35,2 л из имеющихся 48 л, так что остаются неизрасходованными 12,8 л апельсинового сока. Однако запасов виноградного сока не хватает. Требуется для производства 118,8 л, а в наличии всего 108 л. Это и делает план F недопустимым. Вот если бы 12,8 л излишков апельсинового сока обменять на 10,8 л виноградного... Но такие возможности пока не включены в нашу модель.
Эти и другие возможности (если они реальны) можно ввести в
модель. Получается другая модель, с измененной областью допустимых планов, и, соответственно, другим оптимальным планом.
Практика экономико-математического моделирования показывает, что не всегда удается сразу построить хорошую модель. Часто вначале оказываются неучтенными какие-то существенные возможности или ограничения деятельности. Такие возможности обычно вскрываются в ходе проведения постоптимизационного анализа решения задачи. Здесь становится ясной необходимость их введения в модель. Результатом анализа может оказаться изменение модели и новый цикл решения задачи и анализа. Иногда такие циклы приходится проводить неоднократно, пока не получится адекватная модель, хорошо описывающая условия деятельности предприятия.
Мы будем считать для нашего примера, что в модели описаны все существенные условия деятельности, и изменять модель не требуется.
3.4. Ценовой постоптимизационный анализ
Рассмотрим вопрос о том, насколько устойчив оптимальный план к изменению цен на готовую продукцию.
Изменение цен никак не cказывается на области допустимых планов. Цены влияют лишь на положение градиента и, тем самым, на
72
угол наклона линии уровня целевой функции. При достаточно малых изменениях цен наклон градиента и линии уровня изменятся мало. Та вершина области, которая соответствует оптимальному плану (в нашем примере - точка М), будет оставаться оптимальной. Однако при достаточно больших изменениях цен линия уровня повернется настолько, что оптимальный план перейдет в другую, соседнюю вершину (в нашем примере - в точку К или А).
Такой переход в новую вершину соответствует изменению производственного плана. При небольших изменениях цен, как было наиболее выгодно производить 140 л коктейля "Утро" и 30 л коктейля "Вечер", так этот план и остается наиболее выгодным. Какие объемы ресурсов (соков) расходовались на реализацию этого плана, такие и продолжают расходоваться.
При таком изменении цен изменяется лишь величина дохода от продажи произведенной продукции, то есть величина оптимума, но не оптимальный план.
Задача ценового постоптимизационного анализа состоит в том, чтобы определить те критические значения цен, при которых план теряет оптимальность, при которых оптимальной становится другая вершина области допустимых планов. Такие цены являются для производителя продукции сигналом к тому, что пора перестраивать производственный план.
Мы рассмотрим простой случай графического анализа, когда цена на один вид продукции изменяется, а на другой сохраняется. Этот случай является наиболее важным. Более сложная ситуация, когда выпускается не два, а много видов продукции, и цены на все виды меняются одновременно и несогласованно, также может быть полностью проанализирована методами так называемого параметрического программирования.
Начнем с определения критических границ цены первого продукта.
73
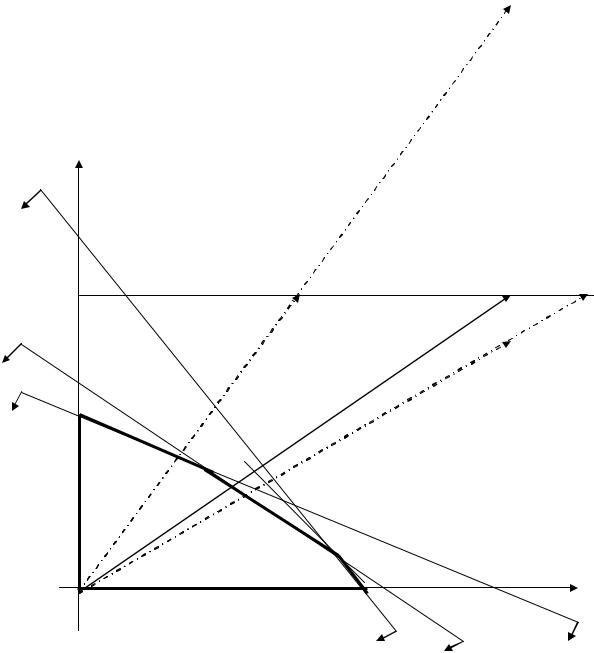
|
x2 |
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
240 |
B |
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
Градиент |
|
|
(3) |
160 |
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
(2) |
120 |
E |
|
|
|
|
|
|
|
|
80 |
|
K |
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
A |
F |
|
D |
|
|
0 |
40 |
80 |
120 |
160 |
|
200 |
240 |
x1 |
|
|
|
|
|
|
(1) |
|
(3) |
(2) |
|
|
Рис.8. Графический ценовой постоптимизационный анализ |
|||||||
Обозначим, как обычно, посредством c1 и c2 цены первого и второго вида продукции (коктейля). В нашем примере c1 = 12, c2 = 10. Пусть значение c1 изменяется, а значение c2 сохраняется. Конец вектораградиента при увеличении c1 будет скользить по горизонтальной прямой
74
направо, при уменьшении c1 - налево (рис.8). Напомним, что при изображении стрелки-градиента мы увеличили масштаб в 20 раз.
При движении направо градиент в некоторый момент окажется перпендикулярен прямой МА - границе первого ограничения. Это критическое положение градиента. В этот момент, то есть при соответствующей цене с1, линия уровня целевой функции будет параллельна прямой МА. При этом значении цены оптимальной точкой будет не только точка М, но и точка А, а также все промежуточные точки отрезка МА. Это и есть критическое значение цены c1, точнее ее верхнее критическое значение. Обозначим его посредством c1в.
Таким образом, если c1 = c1в, то оптимальных планов бесконечно много, они заполняют весь отрезок МА, включая его концы. Такая ситуация с бесконечным множеством оптимальных планов неустойчива. При любом сколь угодно малом отклонении цены c1; от этого критического значения оптимальный план задачи становится единственным. При увеличении цены, отклонении цены вправо от критического значения, единственной оптимальной точкой становится точка А. При уменьшении цены, отклонении ее влево от критического значения, единственной оптимальной точкой является точка М.
Мы рассмотрели процесс увеличения цены c1. Совершенно аналогичное рассуждение связано с уменьшением этой цены. Конец градиента будет при этом скользить по горизонтальной прямой влево, и в некоторый момент градиент займет критическое положение, окажется перпендикулярным прямой КМ, границе третьего ограничения, а линия уровня целевой функции - параллельной этой границе. Этому моменту соответствует нижнее критическое значение цены, c1н.
Таким образом, при c1 = c1н оптимальных планов бесконечно много, они заполняют весь отрезок КМ, включая его концы. Ситуация с бесконечным множеством планов неустойчива. При любом сколь угодно малом увеличении цены, ее отклонении вправо от полученного критического значения, единственной оптимальной точкой является точка
75

М. При сколь угодно малом уменьшении цены, ее отклонении влево от критического значения, оптимальной становится единственная точка К.
Вычислим теперь сами критические значения. Каждое из них соответствует ситуации, когда линия уровня параллельна соответствующей граничной прямой. Линия уровня определяется выражением для целевой функции. Граничная прямая - записью ограничения. Условием параллельности прямых является пропорциональность коэффициентов при одинаковых переменных в уравнениях, задающих эти прямые. Если две прямые заданы уравнениями:
c1 x1 c2 x 2 d
,
a1 x1 a 2 x 2 b
то они параллельны тогда и только тогда, когда
c1 |
|
c |
2 |
. |
|
a1 |
a |
2 |
|||
|
|
Таким образом, для определения нижнего критического значения цены c1 следует использовать условие параллельности линии уровня и границы третьего ограничения, задаваемых уравнениями
c1x1 10x 2 d,
0,125 x1 0,150 x 2 22.
Отсюда получаем:
c1 10 , 0,125 0,150
то есть
c1 0,125 10 8,33. 0,150
Это и есть нижнее критическое значение
76

c1н = 8,33 руб.
Для определения верхнего критического значения c1в.следует использовать условия параллельности линии уровня и границы первого ограничения. Они задаются уравнениями:
c1 x1 10x 2 d,
0,675 x1 0,450 x 2 108.
Условие параллельности определяет пропорцию:
c1 10 . 0,675 0,450
Отсюда
0,675 10
c1 0,450 15.
Таким образом, получено верхнее критическое значение
c1в = 15 руб.
Мы проанализировали границы изменения первой цены при неизменной второй. Рассмотрим теперь изменение второй цены при неизменной первой. Рассуждения здесь совершенно аналогичны по содержанию, но зеркальны по форме.
Пусть цена первого коктейля сохраняет свое значение c1 = 12 руб., а цена второго коктейля c2 изменяется. Конец вектора-градиента будет при этом скользить по вертикальной прямой (рис.8). Сами критические направления градиента (пунктирные стрелки на рис.8) совпадут с теми, которые были получены ранее.
Действительно, эти критические положения соответствуют параллельности линии уровня все той же целевой функции, границам все тех же ограничений. Однако то положение, которое соответствовало нижнему критическому значению одной цены, будет теперь соответствовать верхнему критическому значению другой, и наоборот.
77

Кроме того, сами критические значения цен численно здесь получаются другими, они относятся к цене другого продукта.
Нижнее критическое значение цены с2 определяется из условия параллельности линии уровня и границы первого ограничения
12x1 с2 x 2 d,
0,675 x1 0,450 x 2 108.
Составляем пропорцию
12 с2
0,675 0,450
Отсюда получаем:
0,450 12
c2 0,675 8.
Нижнее критическое значение с2н равно с2н = 8 руб.
Верхнее критическое значение с2 определяется из условия параллельности линии уровня и границы третьего ограничения
12x1 c2 x 2 d,
0,125 x1 0,150 x 2 22.
Пропорция
12 c2
0,125 0,150
позволяет определить:
c2 0,150 12 14,40. 0,125
Верхнее критическое значение равно
с2в = 14,40 руб.
78
Подведем итоги проведенного ценового постоптимизационного анализа. При первоначальных ценах продукции с1 = 12 руб. и с2 = 10 руб. оптимальный план соответствует производству 140 л. коктейля "Утро" и 30 л. коктейля "Вечер" (точка М на рис. 7). Доход бара (оптимум) при этом составит 1980 руб.
Пусть цена с2 второго коктейля сохраняется, с2 = 10 руб. Тогда при изменении цены с1 первого коктейля в промежутке от 8,33 руб. до 15 руб. оптимальный план М сохраняется прежним. Доход бара ZM будет при этом изменяться в зависимости от цены по формуле
Z1M c1 140 10 30 140 c1 300
от своего нижнего до верхнего значения.
Нижнее значение величины дохода Zm1н определяется равенством
ZM |
140 8,33 300 1466,66 |
(руб.) |
1Н |
|
|
Верхнее значение ZM1В рассчитывается аналогично.
ZM |
140 15 300 2400 |
(руб.) |
1В |
|
|
Существующий оптимум, равный 1980 руб., как и следовало ожидать, находится в промежутке между этими значениями.
При снижении цены с1 ниже нижнего критического значения 8,33 руб. оптимальный план резко изменится. Наиболее выгодным станет производить по 80 л коктейля каждого вида (точка К). Доход для такого нового оптимального плана К определится по формуле
Z1K c1 80 10 80 80 c1 800
При повышении цены с1 выше верхнего критического значения 15 руб. оптимальный план также изменится. Наиболее выгодным станет производить один только первый коктейль "Утро" в объеме 160 л (точка А). Доход для такого оптимального плана А определяется по формуле:
Z1A c1 160 10 0 160 c1
79
На границах ценового промежутка оптимальными являются сразу две вершины области допустимых планов (а также все точки соединяющего их отрезка). Формулы для дохода на границах должны быть согласованы, давать одно и то же значение. Должно быть:
ZM |
ZK |
при C C |
8,33, |
|
1 |
1 |
1 |
1н |
|
ZM ZА |
при C C |
15 . |
||
1 |
1 |
1 |
1в |
|
Убедимся в этом. На нижней границе получаем:
Z1M 140c1 300 140 8,33 300 1466 ,66
Z1K 80c1 800 80 8,33 800 1466 ,66
Проведем расчет для верхней границы:
Z1M 140c1 300 140 15 300 2400
Z1K 80c1 800 80 15 800 2400
Таким образом, формулы на границах действительно согласованы. Мы сформулировали результаты анализа изменения цены первого
продукта при неизменной цене второго. Представим теперь результаты анализа изменения цены второго продукта при неизменной цене первого.
Пусть цена с1 первого коктейля сохраняется, с1 = 12. Тогда при изменении цены с2 второго коктейля в промежутке от 8 руб. до 14,40 руб. оптимальный план М сохраняется прежним. Доход бара будет при этом изменяться в зависимости от цены по формуле
ZM2 12 140 c2 30 30 c2 1680
от своего нижнего до верхнего значения.
Нижнее значение дохода ZM2н определится равенством
ZM2Н 30 8 1680 1920 .
Верхнее значение дохода получается аналогично
80
