Chernov_-_Vvedenie_v_LP

Если область допустимых планов задачи пуста, то задача линейного программирования не имеет решения. Нет даже допустимых планов, следовательно, нет и самого лучшего среди них - оптимального.

Как мы увидим, если область неограничена (рис.2), то оптимальный план задачи может существовать, а может и не существовать.

В обычной ситуации ограничена и непуста (рис.1). В этом случае оптимальный план существует и задача состоит в том, чтобы его найти.

2.3.Оптимальный план и оптимум

2.3.1.Линия уровня целевой функции и градиент

Как найти оптимальный план? Обратимся к целевой функции. Приравняем ее какой-нибудь константе d

c1x1 c2 x2 d .

Мы получили уравнение, определяющее некоторую прямую на координатной плоскости. Все точки этой прямой соответствуют одному и тому же значению целевой функции, равному d, одному и тому же уровню значений. Такая прямая называется линией уровня целевой функции. (Понятие линии целевой функции аналогично понятию линии безразличия функции полезности, а также понятию изокванты производственной функции).

При изменении величины d мы получим другую линию уровня, параллельную предыдущей. При увеличении d линия будет смещаться параллельно в одну сторону, при уменьшении - в другую.

Придавая величине d разные конкретные числовые значения, можно понять, какое направление смещения линии уровня соответствует увеличению значения целевой функции, а какое - уменьшению.

Однако, существует более простой способ. А именно, изобразим в координатной плоскости вектор, начало которого находится в начале координат, а конец которого упирается в точку с координатами (c1, c2), где

51

c1 и c2 - коэффициенты при переменных в целевой функции. Такой вектор носит название градиента целевой функции. Этот вектор-градиент перпендикулярен всем линиям уровня целевой функции, а его направление указывает направление роста значений функции.

На рис.1 изображен градиент, направленный внутрь первого координатного угла. Это означает, что коэффициенты c1 и c2 положительны. Разумеется, это не во всех задачах так, в разных задачах знаки этих коэффициентов могут быть различными. Начало градиента всегда располагается в начале координат, но направлен он может быть в любую сторону.

2.3.2.Определение оптимального плана и оптимума

Для того чтобы найти оптимальный план, нужно взять одну из линий уровня, пересекающих область допустимых планов. Затем следует параллельно смещать эту линию в направлении градиента до ее крайнего положения. Крайним называется положение линии уровня, удовлетворяющее двум условиям: во-первых, в этом положении линия уровня еще пересекает область допустимых планов, во-вторых, при любом ее дальнейшем смещении она перестает пересекать эту область.

Точки области допустимых планов, лежащие на одной линии уровня, соответствуют одному и тому же допустимому значению целевой функции. Смещение линии уровня в направлении градиента соответствует росту значений целевой функции. Крайнее положение линии уровня соответствует максимальному допустимому значению целевой функции, то есть оптимуму. Все точки, находящиеся в пересечении области допустимых планов и линии уровня в ее крайнем положении, являются искомыми оптимальными планами.

На рис.1 обозначены пунктиром две линии уровня. Множество оптимальных планов состоит из одной единственной точки - вершины многоугольника, обозначенной посредством X*max .

52

Заметим сразу, что если бы требовалось решать задачу на минимум той же самой целевой функции, то смещать линию уровня следовало бы в направлении уменьшения ее значений, то есть в направлении, противоположном градиенту (или, как иногда говорят, в направлении антиградиента). Линия уровня в новом крайнем положении прошла бы через точку X*min (рис.1).

Если изменить знаки коэффициентов целевой функции c1 и c2 на противоположные, то градиент развернется на 180о, то есть совпадет с антиградиентом первоначальной целевой функции. Если отыскивать минимум этой новой целевой функции с измененными знаками, то следует смещать линию уровня в направлении антиградиента по отношению к новому градиенту, то есть в направлении прежнего градиента. Мы убеждается еще раз, что решение задачи на минимум для целевой функции с измененными знаками соответствует задаче на максимум исходной целевой функции.

2.3.3.Условия разрешимости задачи и единственности

решения

Таким образом, если область допустимых планов непустая и ограниченная, то для каждой из задач — на максимум целевой функции или на минимум целевой функции, существует оптимальный план.

Если же область неограничена, то дело обстоит по-иному. На рис.2 представлен случай, когда существует крайнее положение линии уровня для задачи на минимум. Соответственно, для такой задачи существует и оптимальный план X*min. Однако для задачи на максимум, для смещения линии уровня в направлении градиента, крайнего положения не существует. Как бы далеко ни проходила линия уровня, ее можно сместить еще дальше, и при этом она по-прежнему будет пересекать область допустимых планов. Другими словами, целевая функция на допустимых планах может принимать сколь угодно большие значения. Не существует оптимального плана, то есть допустимого плана с самым

53

большим значением целевой функции. Задача на максимум в таком случае не имеет решения.

Мы рассмотрели случай, когда разрешима задача на минимум, но неразрешима задача на максимум. Разумеется, возможен и противоположный случай, когда разрешима задача на максимум, но неразрешима на минимум. Для этого достаточно в первой задачи изменить знаки коэффициентов целевой функции. Возможен и случай, когда обе задачи неразрешимы. Такая ситуация возникает, например, если градиент на рис.2 развернуть на 90о.

Полученные результаты можно сформулировать следующим образом. Область допустимых планов задачи либо пуста, либо непуста.

Если она пуста, то задача неразрешима, поскольку она не имеет даже допустимых планов.

Если область непуста, то она либо ограничена, либо неограниченна.

Если область ограничена, то задача имеет решение.

Если же область неограниченна, то задача может иметь решение, а может не иметь его. Все зависит в этом случае от того, ограничена ли область в нужном направлении - в том направлении, в котором необходимо смещать линию уровня целевой функции до ее крайнего положения.

Рассмотрим теперь вопросы единственности и неединственности оптимального плана

На рис.1 представлен случай, когда оптимальный план для задачи на максимум (как и для задачи на минимум) является единственным. Линия уровня в своем крайнем положении проходит через единственную точку области допустимых планов. Оптимальный план в данном случае - это угловая точка, вершина многоугольной области допустимых планов. Для того чтобы найти ее координаты, следует определить те полуплоскости, на пересечении границ которых находится интересующая

54

нас вершина. Для этого полезно выписать отдельно соответствующие два неравенства, заменить в них знаки неравенств знаками равенства, и решить получившуюся систему из двух уравнений с двумя неизвестными. Решение системы и даст нам координаты вершины, то есть координаты искомого оптимального плана.

Найдя оптимальный план, мы без труда найдем и величину оптимума. Для этого следует координаты оптимального плана подставить в целевую функцию и провести соответствующие вычисления.

Так следует действовать, когда оптимальный план единственный. Однако возможна и другая ситуация. Линия уровня в своем крайнем положении может содержать целую сторону многоугольной области допустимых планов.

A

B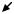

Рис.6. Неединственность оптимального плана

На рис.6 представлен случай, когда градиент перпендикулярен стороне AB, те линии уровня целевой функции параллельны AB. Крайнее положение линии уровня содержит сторону АВ. Это означает, что все точки отрезка АВ, включая его концы, являются оптимальными планами.

55

Оптимальных планов в этом случае бесконечно много. Все они лежат на одной линии уровня и соответствуют одному и тому же значению целевой функции.

Оптимальных планов, как мы видим, может быть бесконечно много, но оптимум всегда единственный. Действительно, из двух различных значений целевой функции одно всегда меньше другого, и поэтому оба вместе не могут быть максимальным (или оба вместе быть минимальными).

Таким образом, оптимальный план задачи может отсутствовать (задача не имеет решения), может быть единственным и может быть неединственным. Можно говорить о множестве оптимальных планов, которое может быть пустым, или содержать один элемент, или содержать бесконечное множество элементов.

2.3.4.Свойства множества оптимальных планов.

Множество оптимальных планов является выпуклым (как и множество допустимых планов). Если два оптимальных плана соединить отрезком прямой, то все точки этого отрезка также окажутся оптимальными. Например, если на рис.6 среди оптимальных планов выбрать какие-нибудь два, A1 и B1, то все точки отрезка A1B1, являясь одновременно точками отрезка АВ, будут оптимальными. Все они лежат на одной и той же линии уровня в ее крайнем положении.

Из выпуклости этого множества следует, что любая смесь (взвешенная сумма) двух оптимальных планов также является оптимальным планом. Отсюда следует также, что для множества оптимальных планов задачи линейного программирования имеются лишь три возможности: либо это множество пусто (оптимальных планов нет, задача неразрешима), либо состоит из одного элемента (оптимальный план единственный), либо оно бесконечно. Действительно, если существует хотя бы два различных оптимальных плана, то и все

56

бесконечное множество точек соединяющего их отрезка состоит из оптимальных планов.

Мы видим, что возможна ситуация, когда оптимальный план не является вершиной области допустимых планов. Однако можно доказать, что среди оптимальных планов обязательно присутствует хотя бы одна вершина (на рис.6 таких вершин две: А и В). Если же оптимальный план единственный, то он непременно является вершиной.

Отсюда следует важный вывод. Для того чтобы найти оптимальный план, достаточно исследовать не все бесконечное множество допустимых планов, а лишь конечное множество вершин области допустимых планов.

Мы рассмотрели геометрический смысл задачи с двумя переменными. Для задач с тремя переменными можно провести аналогичное рассуждение. Вместо полуплоскостей с граничной прямой необходимо будет рассматривать полупространства с граничными плоскостями. Вместо многоугольной области на плоскости - многогранную область в пространстве. Вместе линии уровня на плоскости - плоскость уровня в пространстве. Представление ситуации будет менее наглядным.

Для задач с большим числом переменных наглядность и вовсе будет утрачена. Графический метод решения для таких задач оказывается непригодным. Необходимо использовать уже другие, не геометрические, а аналитические, расчетные методы.

Такие методы существуют. Наиболее известным среди них является так называемый симплекс-метод. Этот метод позволяет решить любую задачу линейного программирования (либо доказать ее неразрешимость). Он лежит в основе разнообразных алгоритмов расчета оптимального плана. Известны многочисленные компьютерные реализации таких алгоритмов. Один из удобных вариантов встроен в Excel. Для проведения соответствующих расчетов следует обратиться в Excel к встроенной процедуре «Поиск решения».

57

Геометрический подход, изученный нами для задачи с двумя переменными, позволяет не только решать такие задачи, но и глубже понять ход решения задачи с большим числом переменных, в тех ситуациях, когда непосредственная геометрическая наглядность оказывается утраченной.

2.4. Пример графического решения задачи

Приведем графическое решение задачи об изготовлении коктейлей из соков в баре. Напомним математическую модель этой задачи.

Изобразим данные по этой модели в системе координат (рис.7). Сначала изобразим границу полуплоскости, соответствующую

множеству решений первого неравенства. Для этого неравенство заменим равенством:

0,62x1 0,450x 2 108 .

Множество решений этого уравнения соответствует прямой на координатной плоскости.

Чтобы изобразить прямую достаточно найти две ее точки. Найдем точки на осях координат. Для этого положим в уравнении x2 = 0. Получим x1 = 160. Изобразим соответствующую точку на оси OX1 (точка А на рис.7). Теперь положим в уравнении x1 = 0. Получим x2 = 240. Изобразим точку на оси OX2.

58

Соединим точки А и В прямой. Мы получили граничную прямую искомой полуплоскости.

Эта прямая делит координатную плоскость на две полуплоскости. Для того чтобы, определить ту полуплоскость, которая соответствует множеству решений рассматриваемого неравенства, следует выбрать любую точку плоскости, не лежащую на граничной прямой, и подставить ее координаты в наше неравенство. Если неравенство окажется верным, то выбранная точка принадлежит искомой полуплоскости, если неверным - то она принадлежит другой полуплоскости.

Выберем, например, в качестве такой точки точку 0 - начало координат. Подставим ее координаты в левую часть неравенства.

Получим 0 108. Неравенство верное. Следовательно, искомой

59

полуплоскостью является та, которая содержит начало координат и тем самым лежит слева от граничной прямой.

Если бы мы вместо начала координат взяли, например, точку с координатами (1000, 1000), лежащую правее и выше нашей прямой, и подставили бы ее координаты в левую часть неравенства, то получили бы

1125 108. Неравенство неверно, следовательно, выбранная точка не принадлежит искомой полуплоскости. Искомой оказывается все та же левая полуплоскость.

Найденная полуплоскость отмечена стрелками около точек пересечения граничной прямой с осями координат.

Теперь найдем полуплоскость, соответствующую второму неравенству системы ограничений. Ее граничная прямая проходит через точку D с координатами (240; 0), лежащую на оси Ox1, и через точку Е с координатами (0; 120) на оси Ox2. Из двух возможных полуплоскостей опять следует выбрать ту, которая содержит начало координат.

Граница третьего ограничения проходит через точку F на оси Ox1 с координатами (176; 0) и через точку G на оси Ox2 с координатами (0; 440/3) (0; 146,67). Искомой полуплоскостью снова оказывается та,

которая содержит начало координат.

Наконец, условие x1 0 определяет правую полуплоскость,

граничная прямая которой совпадает с осью Ox2, а условие x2 0

определяет верхнюю полуплоскость с граничной прямой Ox1.

Система ограничений в целом определяет пересечение всех полученных полуплоскостей, то есть многоугольник ОЕКМА. Этот пятиугольник и является областью допустимых планов нашей задачи.

При построении области допустимых планов мы не обращались к целевой функции. Для определения оптимального плана необходимо привлечь целевую функцию. Так мы и поступим. Однако кое-что про оптимальный план можно сказать уже сейчас.

Во-первых, область допустимых планов непуста и ограничена. Следовательно, оптимальный план существует.

60