4. Расчет основных статистик и оценка корреляционной связи (Задача №2)

В работе необходимо рассчитать основные статистики.

1. Средние величины. В практическом занятии рассчитывается показатель средней арифметической:

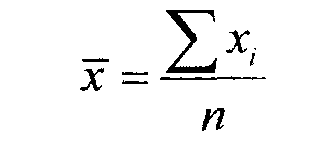
где хi, - значение признака; n - объем совокупности.

2. Размах вариации.

где х_max- максимальное значение признака; х_min - минимальное значение признака.

3. Среднее линейное отклонение.

4. Дисперсия признака.

5. Среднее квадратичное отклонение.

6. Коэффициент вариации.

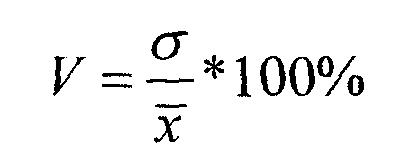
7. Линейный коэффициент корреляции.

Измерение тесноты и направления связи признаков друг с другом является важнейшей задачей статистического исследования социально-экономических явлений. Тесноту и направление связи между признаками можно измерить с помощью линейного коэффициента парной корреляции, который рассчитывается по следующей формуле:

8. Множественный коэффициент корреляции.

Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками. Для оценки тесноты связи между результативным и двумя факторными признаками множественный коэффициент корреляции рассчитывается по формуле:

Коэффициент корреляции - это показатель, оценивающий тесноту линейной связи между признаками. Он может принимать значения от -1 до +1. Знак "-" означает, что связь обратная, "+" - прямая. Чем ближе коэффициент к 1 тем теснее линейная связь. Коэффициент =1 означает, что связь между признаками функциональная. Теснота связи оценивается по величине коэффициента корреляции [8]:

если | r | ≤ 0.3 , то связь слабая или совсем отсутствует (необходимы дополнительные исследования статистической значимости коэффициентов);

если 0.3 ≤ | r | ≤ 0.5, связь умеренная;

если 0.5 ≤ | r | ≤ 0.7, значительная;

если 0.7 ≤ | r | ≤ 0.9, тесная;

если > 0.91, очень тесная.

Для практических целей Дворецкий рекомендует использовать значительные, тесные и очень тесные связи.

По величине коэффициента корреляции оцениваем связь между результативными и факторными признаками. Если коэффициент корреляции равен нулю, то линейная связь отсутствует, если коэффициент корреляции положителен, то связь между признаками прямая, если отрицателен, то связь между признаками обратная,

Значение множественного коэффициента корреляции лежит в диапазоне от 0 до 1 и тоже оценивается с помощью приведенных выше диапазонов положительных значений коэффициента корреляции.

9. Нормирование данных.

Нормирование позволяет привести показатели с разной физической сущностью и разными единицами измерения к единому формату в диапазоне от 0 до 1. Нормирование осуществляется путем деления модуля (абсолютной величины) всех членов выборки на максимальную величину данной выборки:

.

Выполнение задачи с использованием Excel

1. Ввод исходных данных в таблицу Excel. При наличии электронной версии данного методического пособия для этого используется операция копирования из среды Word. Вводятся исходные данные (см. табл. 2.1): «№ периода» (столбец 1); «Уровень безработицы, %» (столбец 2), «Уровень инфляции» (столбец 3), «Реальный ВВП, трлн. руб.» (столбец 4), «Объем промышленного производства, трлн. руб.» (столбец 5), «Объем капитального строительства, трлн. руб.» (столбец 6), «Средняя заработная плата, трлн. руб.» (столбец 7), «Располагаемый доход, млрд руб.» (столбец 8), «Потребительские расходы, млрд. руб.» (столбец 9), «Количество туристов за рубежом России, тыс. чел.» (столбец 10). Координаты матрицы данных в примере табл. 2.1 – А3 : J10.

При расчете статистических показателей в Excel 2007 используются формула находящиеся: «Формулы», «Другие функции», «Статистические». Если исходные данные будут помещены

1. Расчет средних значений показателей.

• В конце столбца 1 (ячейка А11) вводится наименование показателя - «Среднее»;

• В ячейку справа вводится формула расчета среднего «=СРЗНАЧ(B3:B10)» (диапазон расчета среднего вводится мышью);

• Формула копируется для всех других макроэкономических показателей (других столбцов).

1. Расчет показателя размах.

• Вводится название показателя – «Размах» (ячейка А12);

• В ячейку справа вводится формула расчета «=МАКС(B3:B10)-МИН(B3:B10)»;

• Формула копируется для всех других столбцов.

1. Расчет среднего линейного отклонения.

• Вводится название показателя – «Среднее линейное» (ячейка А13).

• В ячейку справа вводится формула расчета «=СРОТКЛ(B3:B10).

• Формула копируется для всех других столбцов.

1. Расчет дисперсии.

• Вводится название показателя – «Дисперсия» (ячейка А14);

• В ячейку справа вводится формула расчета: «=ДИСП(B3:B10)»;

• Формула копируется для всех других столбцов.

1. Расчет среднего квадратичного отклонения.

• Вводится название показателя «Среднее квадратичное отклонение» (ячейка А15);

• В ячейку справа вводится формула расчета: «=КОРЕНЬ(B14)».

• Формула копируется для других столбцов.

1. Расчет коэффициента вариации.

• Вводится название показателя «Коэффициент вариации» (ячейка А16).

• В ячейку справа вводится формула расчета: «=B15*100/B11».

• Формула копируется для всех других столбцов.

1. Расчет значений линейных коэффициентов парной корреляции.

• В ячейку В17 вводится название таблицы «Коэффициентов парной корреляции» (см. табл. 2.2);

• В ячейку В19 вводится формула: «=КОРРЕЛ($B2:$B16;B2:B16». Координаты первого диапазона даны по буквенной координате в абсолютном виде (знак $), для возможности копирования формулы по всем другим показателям (столбцам). Формула копируется для всех других столбцов;

• В ячейки В20 – В28 вводятся соответственно формулы: «=КОРРЕЛ($C3:$C10;B3:B10)», «=КОРРЕЛ($D3:$D10;B3:B10)», «=КОРРЕЛ($E3:$E10;B3:B10)», «=КОРРЕЛ($F3:$F10;B3:B10)», «=КОРРЕЛ($G3:$G10;B3:B10)», «=КОРРЕЛ($H3:$H10;B3:B10)», «=КОРРЕЛ($I3:$I10;B3:B10)», «=КОРРЕЛ($J3:$J10;B3:B10)». Формула копируется для всех других столбцов;

• В полученных коэффициентах корреляции (см. табл. 2.2) выделяются два коэффициента наибольших по модулю связанных с показателем «Количество туристов за рубежом России» (выделены серым цветом и жирным шрифтом).

9. Расчет множественного коэффициента корреляции.

Расчет производится по формуле, приведенной выше:

«=КОРЕНЬ((СТЕПЕНЬ(E28;2)+СТЕПЕНЬ(F28;2)-2*F28*E28*E24)/(1-СТЕПЕНЬ(E24;2))), где E28 и F28 координаты коэффициентов с наибольшими значениями по модулю, а E24 коэффициент парной корреляции между этими коэффициентами. Внимание! В конкретных заданиях координаты ячеек возможно будут другими.

Расчетное значение множественного коэффициента корреляции сравнивается с предельными значениями приведенными выше и определяется теснота связи.

1. Нормирование и визуализация исходных данных.

• В ячейку В30 вводится название таблицы «Нормированные исходные данные» (см. табл. 2.3);

• В ячейку В32 вводится формула «=B3/МАКС(B$3:B$10)»;

• Формула копируется для всех других ячеек в диапазоне В32:J39.

• Рассчитываются статистики аналогично тому, для этого целесообразно скопировать сразу все ячейки А11: J16;

• На основании полученных нормированных исходных данных строится график динамики изменения показателей в одном и том же масштабе 0 -1, см. рис. 4.1.