Определение среднего абсолютного прироста, средних темпов роста и прироста

По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста.

Средний абсолютный прирост может быть получен по одной из формул:

или ,

где n - число уровней ряда динамики;

- первый уровень ряда динамики;

- последний уровень ряда динамики;

- цепные абсолютные приросты.

Средний темп роста можно определить, пользуясь формулами:

где n - число рассчитанных цепных или базисных темпов роста;

- уровень ряда, принятый за базу для сравнения;

- последний уровень ряда;

- цепные темпы роста (в коэффициентах);

- первый базисный темп роста;

- последний базисный темп роста.

Между темпами прироста и темпами роста К существует соотношение= К - 1, аналогичное соотношение верно и для средних величин.

Определение в рядах динамики общей тенденции развития

Определение уровней ряда динамики на протяжении длительного периода времени обусловлено действием ряда факторов, которые неоднородны по силе и направлению воздействия, оказываемого на изучаемое явление.

Рассматривая динамические ряды, пытаются разделить эти факторы на постоянно действующие и оказывающие определяющее воздействие на уровни ряда, формирующие основную тенденцию развития, и случайные факторы, приводящие к кратковременным изменениям уровней ряда динамики. Наиболее важна при анализе ряда динамики его основная тенденция развития, но часто по одному лишь внешнему виду ряда динамики ее установить невозможно, поэтому используют специальные методы обработки, позволяющие показать основную тенденцию ряда. Методы обработки используются как простые, так и достаточно сложные. Простейший способ обработки ряда динамики, применяемый с целью установления закономерностей развития - метод укрупнения интервалов.

Суть метода укрупнения интервалов в том, чтобы от интервалов, или периодов времени, для которых определены исходные уровни ряда динамики, перейти к более продолжительным периодам времени и посмотреть, как уровни ряда изменяются в этом случае.

Пример. Данные о реализации молочной продукции в магазинах города по месяцам представлены таблицей 1.27 (в тоннах).

Таблица 8.2

месяц	2004	2005	2006
январь	5,3	5,3	5,4
февраль	5,3	5,1	5,2
март	7,9	8,3	8,2
апрель	8,2	9,0	9,3
май	9,8	9,5	10,1
июнь	12,5	13,0	13,1
июль	11,8	12,2	12,5
август	10,3	10,4	10,8
сентябрь	8,2	8,0	8,3
октябрь	6,5	6,6	6,8
ноябрь	5,4	5,5	5,7
декабрь	5,5	5,5	5,6
итого за год	96,7	98,4	101

Исходные уровни ряда динамики подвержены сезонным изменениям; для определения общей тенденции развития переходят от ежемесячных уровней к годовым уровням: 2004 г. - 96,7 тонн; 2005 г. - 98,4 тонн; 2006 г. - 101 тонна. Эти цифры, полученные в результате перехода к годовым уровням ряда динамики, показывают общую тенденцию роста реализации молочной продукции.

Другой способ определения тенденции в ряду динамики – метод скользящих средних. Суть метода заключается в том, что фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу, например: – исходные или фактические уровни ряда динамики заменяются средними уровнями:;;; …….

В результате получается сглаженный ряд, состоящий из скользящих пятизвенных средних уровней . Между расположением уровнейиустанавливается соответствие:, – –– – , сглаженный ряд короче исходного на число уровней, гдеk - число уровней, выбранных для определения средних уровней ряда.

Сглаживание методом скользящих средних можно производить по четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней. Полученные при этом средние уровни называются четырёхзвенными скользящими средними, пятизвенными скользящими средними и т.д.

При сглаживании ряда динамики по чётному числу уровней выполняется дополнительная операция, называемая центрированием, поскольку, при вычислении скользящего среднего, например по четырём уровням, относится к временной точке между моментами времени, когда были зафиксированы фактические уровнии. Схема вычислений и рас положений уровней сглаженного ряда становится сложнее:

... – исходные уровни;

– – ... – сглаженные уровни;

– – ... – центрированные сглаженные уровни;

.

Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление.

Пример.

Таблица

Годы	Объем продаж, млн. руб.	Скользящая средняя по 5 уровням
1960	4,3	–
1961	4,5	–
1962	4,3	4,72
1963	5,2	5,00
1964	5,3	5,30
1965	5,7	5,64
1966	6,0	5,78
1967	6,0	5,86
1968	5,9	6,10
1969	5,7	6,32
1970	6,9	6,58
1971	7,1	6,94
1972	7,3	7,48
1973	7,7	7,68
1974	8,4	7,92
1975	7,9	8,22
1976	8,3	8,38
1977	8,8	8,54
1978	8,5	8,94
1979	9,2	9,18
1980	9,9	9,30
1981	9,6	–
1982	9,3	–

На рис. показан график, построенный по данным о объеме продаж представленных в таблице 8.2.

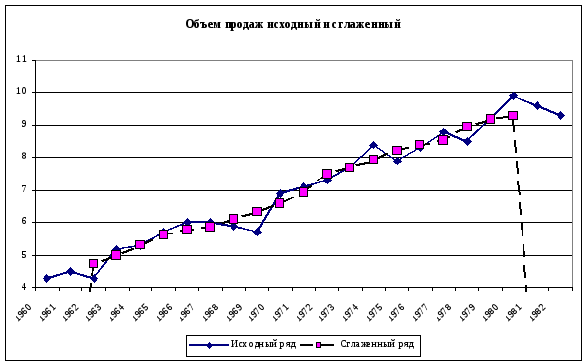
Рис. 8.1. Объем продаж исходный и сглаженный

Наиболее совершенным способом определения тенденции развития в ряду динамики является метод аналитического выравнивания. При этом методе исходные уровни ряда динамики заменяются теоретическими или расчетными, которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др.

Например, ,

где - коэффициенты, определяемые в методе аналитического выравнивания;

- моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами .

Расчет коэффициентов ведется на основе метода наименьших квадратов:

Если вместо подставить(или соответствующее выражение для других математических функций), получим:

Это функция двух переменных (всеиизвестны), которая при определенныхдостигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов.

Для прямой:

где n – число моментов времени, для которых были получены исходные уровни ряда .

Если вместо абсолютного времени выбрать условное время таким образом, чтобы, то записанные выражения для определенияупрощаются:

Пример. Нечетное число уровня ряда.

1981	1982	1983	1984	1985	1986	1987	абсолютное время
-3	-2	-1	0	1	2	3	условное время

Чётное число уровней ряда.

1981	1982	1983	1984	1985	1986	1987	1988	абсолютное время
-7	-5	-3	-1	1	3	5	7	условное время

В обоих случаях .

Пример. Выполняется аналитическое выравнивание ряда, отражающего производство стали в стране по годам (млн. т).

1985	1986	1987	1988	1989
141,3	144,8	146,7	151,5	149,0

В качестве математической функции, отражающей тенденцию развития, выбирается прямая , определениепроизводится для условного времени, в результате,.

Год	Производство стали	Условное время,	Теоретические уровни
1985	141,3	-2	142,2
1986	144,8	-1	144,4
1987	146,7	0	146,7
1988	151,5	1	148,9
1989	149,0	2	151,1