Динамика оказание услуг по четырем месяцам, тыс. Руб.

День	№ декады
	1	2	3	4	5	6	7	8	8	10	11	12
1	5,29	4,86	4,60	5,07	4,58	4,22	5,22	5,01	5,34	5,76	5,97	4,40
2	5,66	5,88	4,79	4,78	4,40	5,47	4,80	4,40	4,82	4,75	5,27	5,31
3	4,80	4,15	4,70	4,95	5,05	4,49	4,63	4,73	5,10	4,81	4,27	5,58
4	5,52	5,67	5,03	5,44	4,82	4,93	4,83	4,76	5,27	4,30	5,64	5,79
5	5,89	6,16	4,05	5,18	4,78	5,36	4,86	4,89	5,32	5,39	4,68	4,75
6	6,03	4,41	5,68	5,33	5,07	5,23	4,35	5,24	4,99	4,12	4,47	5,49
7	5,11	5,67	4,39	4,86	5,19	5,01	5,80	5,09	5,61	5,25	5,13	5,56
8	4,35	5,22	4,81	5,41	5,80	4,91	4,52	4,51	5,13	4,95	4,85	6,24
9	4,57	4,99	4,96	4,96	4,75	5,19	5,21	4,19	5,12	4,92	5,23	4,79
10	5,22	5,34	4,27	5,08	4,12	5,52	5,47	5,18	4,61	5,42	4,53	4,97

Рис. 5.1 Динамика продаж услуги, тыс. руб.

В результате исходные данные преобразуются в частотный вид см. табл. 5.3.

Таблица 5.3

Частотная интерпретация исходных данных

Возраст оборудования, тыс. руб.	Количество дней (fi)	Середина интервала хi
7,3 – 7,7	8	7,5
7,7 -8,1	11	7,9
8,1 – 8,5	10	8,3
8,5 – 8,9	24	8,7
8,9 – 9,3	21	9,1
9,3 -9,7	21	9,5
9,7 – 10,1	11	9,9
10,1- 10,4	10	10,3
10,4 – 10,8	3	10,6
10,8 -11,2	3	11

На основании таблицы построена гистограмма, рис. 5.2.

Рис. 5.2. Гистограмма распределения частот дневных выручек

Следует иметь ввиду, что самый быстрый способ преобразования временного ряда в частотный использования пакета Statistica. Для этого исходные данные копируются в пакет, а затем нажимая кнопку «Граф» в выпавшем меню выбирается оция «Гистограмма» и в ней определяется число групп («Категория» в нашем случае 10), «Тип графика» Обычный «Variables» (Данные) – соответствующий столбец с данными. OK. В построенной гистограмме можно поставить значение частот для этого при нахождении курсора гистограмме в меню вызванном правой клавишей выбирает опцию «Метки точки» кликнуть на окне «Показать метки» и кликнуть на окне «Счет».

Решение

Средне дневная реализация определяется x_ср=∑(x_i*f_i)/∑f_i = 1370/100=13,7 тыс.руб.

Мода (Мо) – значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту (частость).

В дискретном ряду мода определяется визуально по максимальной частоте или частости.

В интервальном ряду по наибольшей частоте определяется модальные интервал (например, по данным таблицы наибольшая частота f_max= 30%, а модальный интервал Мо=10-15 тыс. руб.), а конкретное значение моды в модальном интервале определяется:

,

где x_o и h –соответственно нижняя граница и величина модального интервала (например, по данным таблицы x_o =10 тыс.руб, а h=(20-15)=5 тыс.руб., см. рис. 3.3);

f_M0 – частота (частность) модального интервала (по данным таблицы f_M0 =30%, f_Mo-1=19% f_Mo+1=24% соответственно значение моды: Mo=10+5(30-19)/[(30-19)+(30-24)]=13.24 тыс.руб.).

Медиана (Ме) – значение признака (варианта), приходящееся на середину ранжированной (упорядоченной) совокупности, т.е. это вариант, который делит ряд распределения на две равные по объему части.

Медиана, как и мода, не зависит от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределенными границами.

Для определения медианы в ранжированном ряду необходимо вначале найти номер медианы: N=(n+1)/2 (в нашем случае N=(100+1)/2=50.5%, см. рис. 5.4). Затем по накопленным (кумулятивным) частотам S_i дискретного ряда определяется медиальный интервал (в нашем случае интервал совпадает с модальным интервалом (такое совпадение не всегда обязательно, но встречается часто) это 10 – 15 тыс.руб, поскольку ближайшая большая 50% накопленная частота S_i = 59%).

Рис. 5.3. Гистограмма и полигон

В дискретном ряду распределения медианы находится непосредственно по накопленной частоте, соответствующей номеру медианы.

В случае интервального (вариационного) ряда распределения конкретного значение медианы вычисляется по формуле:

где x_o и h –соответственно нижняя граница и величина медианного интервала (по данным таблицы x_o =10 тыс.руб., а h=(15-10)=5 тыс.руб.);

f_Me – частота (частность) медианного интервала (по данным таблицы f_Me=30%);

S_Me-1 – накопленная частота предмедиального интервала (S_Me-1= 29%).

Значение медианы для примера из таблицы Ме=10+5(50-29)/30=13,5 тыс. руб. Откуда можно заключить, что половина всего оборудование имеет возраст не более 13,5 тыс.руб. или половина всего оборудования имеет возраст больше 13,5 тыс.руб.

В симметричных рядах распределение значения моды и медианы совпадают со вредней величиной , а в умеренно асимметричных рядах они соотносятся:.

Кроме медианы в анализе закономерностей распределения используются также квартели и децели, при расчете которых в формуле расчета медиального значения Ме множитель ½ заменяется на 0,25 и 0,1 соответственно.

Показатели степени вариации и способы их расчета. Для измерения и оценки вариации используют абсолютные и относительные характеристики.

Наиболее поверхностная оценка рассеяния (вариации) совокупности распределения определяется с помощью вариационного размаха R, который показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака: R=x_max-x_min.

Рис. 5.4. Кумулята

Среднее линейное отклонение является обобщающей мерой вариации индивидуальных значений признака от средней арифметической величины. Она дает абсолютную меру вариации.

Для интервальных (вариационных) рядов взвешенная средняя определяется:

Для приведенного выше примера - =531,6/100=5,32 тыс.руб.

Дисперсия ()² – это средний квадрат отклонений индивидуальных значений признака от средней величины. Дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, а также для проверки статистических гипотез.

Для приведенного выше примера - =4256/100=42,56.

Среднее квадратическое отклонение -  представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней, т.е. оно исчисляется путем извлечения квадратного корня из дисперсии и измеряется в тех же единицах, что и варьирующий признак.

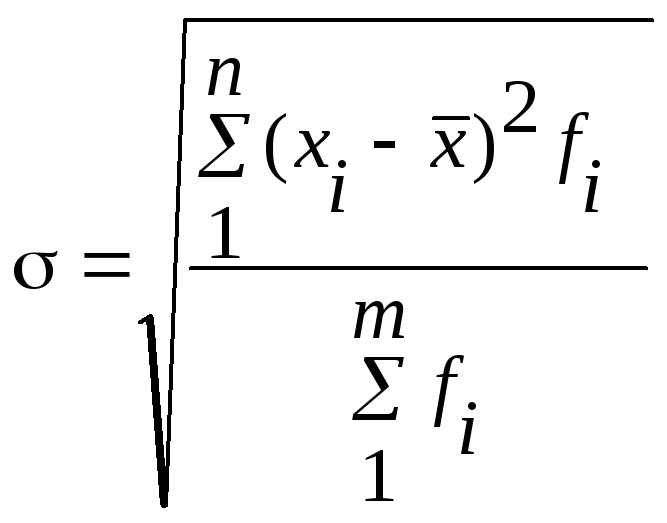
Для приведенного выше примера - =6 тыс.руб.

Коэффициент осцилляции:

Для приведенного выше примера - =182,48%.

Линейный коэффициент вариации:

Для приведенного выше примера - = 36,5%.

Коэффициент вариации:

Для приведенного выше примера = 43,8 %.

Показатели асимметрии и эксцесса. Симметричным называется распределение у которого частоты равноотстоящие от моды равны между собой, следовательно выполняется соотношение =Мо=Ме. Соответственно наиболее простой мерой асимметрии является (x_ср-Мо).

Коэффициент асимметрии Пирсона:

При К_а>0 скошенность ряда правосторонняя (т.е. >Mo), при К_а<0 скошенность ряда левосторонняя (т.е. <Mo). В нашем примере К_а=0,08 и следовательно ряд характеризуется правосторонней незначительной асимметрией.

Нормальный коэффициент асимметрии третьего порядка. Часто используется в прикладных расчетах. Коэффициент не зависит от масштаба, выбранного при измерении варианта, так как является отвлеченной величиной и определяется по формуле:

,

где - центральный момент третьего порядка и определяется:

Для случая из таблицы 4 нормальный коэффициент асимметрии третьего порядка будет равен А₃=412,64/216 =1,91.

Нормальный коэффициент асимметрии четвертого порядка. Используется для определения «крутизны» («заостренности») графика распределения частот. Определяется по формуле:

,

где - центральный момент третьего порядка и определяется:

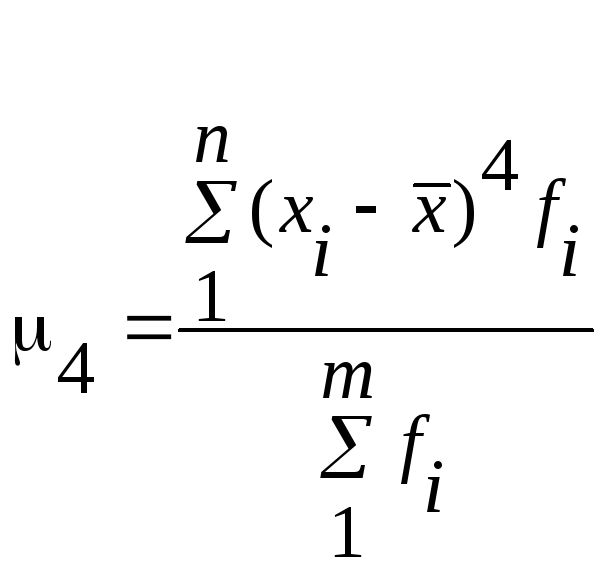
При нормальном распределении А₄=3. Для измерении асимметрии эталоном служит симметричное (нормальное) распределение, для которого А₃=0.

Для случая из таблицы 4 нормальный коэффициент асимметрии четвертого порядка будет равен А₄=3,42.

Показатель эксцесса распределения:

.

При Е_k>0 распределение островершинное, при Е_k <0 – плосковершинное.

В нашем примере Е_k=(3,42-3)=0,42 и следовательно ряд островершинный.