Варианты по дискриминантному анализу

Номер варианта	Номер испытуемого
	группа X	группа Y
1	1, 2, 3, 6	8, 9, 10, 11, 12
2	1, 2, 3, 4	9, 10, 11, 12, 13
3	1, 2,3, 5	11, 12, 13, 14, 15
4	1, 2, 5, 7	8, 12, 13, 14, 15
5	2, 5, 6, 7	8, 9, 10, 14, 15
6	2, 3, 4, 5	10, 11, 12, 13, 14
7	1, 5, 6, 7	9, 10, 11, 14, 15
8	1, 3, 4, 5	8, 10, 13, 14, 15
9	1, 2,4, 5	8, 9, 10, 11, 15
10	2, 3, 4, 7	8, 9, 10, 11, 13

Задача 10. Для классификации шести испытуемых (мужчин-руководителей), характеризуемых четырьмя показателями состояния личности (X₁, X₂, X₃ , Х₄), требуется:

1) найти матрицу нормированных значений исходных данных Z;

2) построить матрицу расстояний между наблюдениями;

3) реализовать иерархическую агломеративную процедуру кластерного анализа;

4) построить дендрограмму.

Варианты задач и значения показателей состояния личности даны в таблицах.

Таблица. Варианты заданий по кластерному анализу

Номер варианта	Номера испытуемых
1	3, 5, 6, 7, 8,10
2	2, 3, 5, 6, 7,13
3	1, 3, 6, 7, 8,15
4	2, 6, 7, 8,10,13
5	1, 8, 9,10,11,15
6	2, 7, 9,13,14,15
7	3, 6, 7, 9,13,15
8	1, 6, 7,10,12,15
9	2, 5, 9,13,15,14
10	1, 4, 9,10,14,15

Таблица. Значение показателей состояния личностей

№	X1	X2	X3	X4
1	0,33	0,6	1.11	0.54
2	0,33	0,2	0,44	0.31
3	0,17	0,6	0,33	0.10
4	0,23	0,3	0,67	0.15
5	0,83	0,4	1.33	0.15
6	0,75	0,6	0,56	0.15
7	0,92	0,9	1.11	0.92
8	0,42	0,4	0,33	0.15
9	1,08	1.3	1.56	1.38
10	0,17	0,8	0,22	0.31
11	0,08	0,5	0,67	0.08
12	0.33	0,3	0,67	0.31
13	0,22	0,3	0,44	0.15
14	1.08	1,0	1.22	1,00
15	1.00	1,0	1.22	0.77

Обозначения и наименования показателей: X₁ - соматизация у мужчин; X₂ - обессивность-импульсивность у мужчин; X₃ – межличностная сензетивность у мужчин; X₄ - депрессия у мужчин.

Примеры решения задач

Задача 1. В исследовании изучалась проблема психологических барьеров при обращении в службу знакомств у мужчин и женщин. В эксперименте участвовали 14 мужчин и 18 женщины в возрасте от 17 до 45 лет. Испытуемые должны были отметить на отрезке точку, соответствующую интенсивности внутреннего сопротивления, которое им пришлось преодолеть, чтобы обратиться в службу знакомств. Длина отрезка, отражающая максимально возможное сопротивление, составляла 100 мм.

Можно ли утверждать, что мужчинам приходится преодолевать субъективно более мощное сопротивление?

Табл. 1.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
М	71	79	75	75	68	80	57	54	34	28	25	46	29	44	0	0	0	0
Ж	48	44	23	11	65	68	56	39	55	55	24	19	18	65	59	31	42	57

Решение. Поскольку в обеих выборках n₁, n₂ > 11 и диапазоны разброса значений в двух выборках не совпадают между собой, для сопоставления двух выборок воспользуемся критерием Q Розенбаума. Объемы выборок различаются менее чем на 10 человек, следовательно, ограничение о примерном равенстве выборок соблюдается.

Упорядочим данные по возрастанию признака (табл.2).

Табл. 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
М	80	79	75	75	71	68	57	54	46	44	34	29	28	25
Ж	68	65	65	59	57	56	55	55	48	44	42	39	31	24	23	19	18	11

Первым, более высоким, рядом является ряд значений в мужской выборке.

Средняя величина тоже выше в выборке мужчин.

Сформулируем гипотезы.

H₀: При обращении в службу знакомств мужчинам приходится преодолевать не более интенсивное внутреннее сопротивление, чем женщинам.

H₁: При обращении в службу знакомств мужчинам приходится преодолевать более интенсивное внутреннее сопротивление, чем женщинам.

Сопоставим ряды значений для определения S₁ и S₂.

В Табл. 2 отмечены два интересующих нас значения: максимальное значение 2-го ряда (max 2) и минимальное значение 1-го ряда (min 1).

Определим S₁, как количество значений 1-го ряда, которые превышают максимальное значение 2-го ряда: S₁=5.

Определяем S₂, как количество значений 2-го ряда, которые меньше минимального значения 1-го ряда: S₂=5.

Вычисляем эмпирическое значение Q_эмп по формуле

Q_эмп = S₁ + S₂ = 5+5 =10

По таблице Приложения 1 определяем критические значения Q для n₁ = 14, n₂ = 18:

Так как Q_эмп > Q_кр гипотеза H₀ отклоняется. Принимается гипотеза H₁.

Ответ. При обращении в службу знакомств мужчинам приходится преодолевать более интенсивное внутреннее сопротивление, чем женщинам.

Задача 2. В эксперименте по исследованию интеллектуальной настойчивости испытуемым было предложено решить три анаграммы. Время, затраченное на решение анаграмм, фиксировалось. Достоверны ли различия во времени решения различных анаграмм испытуемыми?

	Анаграмма 1 КРУА (РУКА)	Анаграмма 2 АЛСТЬ (СТАЛЬ)	Анаграмма 3 ИНААМШ (МАШИНА)
1	3	7	6
2	7	8	8
3	5	4	5
4	4	5	9
5	6	7	8

Решение.

Проранжируем значения, полученные по трем анаграммам каждым испытуемым. Например, первый испытуемый меньше всего времени провел над анаграммой 1 - следовательно, она получает ранг 1. На втором месте у него стоит анаграмма 3 - она получает ранг 2. Наконец, анаграмма 2 получает ранг 3, потому что она решалась им дольше двух других.

Испытуемый	Анаграмма 1		Анаграмма 2		Анаграмма 3		Суммы
	Время	Ранг	Время	Ранг	Время	Ранг
1	3	1	7	3	6	2
2	7	1	8	2	8	3
3	5	2	4	1	5	3
4	4	1	5	2	9	3
5	6	1	7	2	8	3
		6		10		14	30
Квадрат 		36		100		196	332

Сформулируем гипотезы.

Н₀: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, являются случайными.

H₁: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, не являются случайными.

Теперь нам нужно определить эмпирическое значение ²_r по формуле:

где с - количество условий;

п - количество испытуемых;

T_j - суммы рангов по каждому из условий

Определим ²_r для условий нашей задачи:

По таблице Приложения 2 для эмпирического значения ²_r определяем уровень значимости р=0,0039.

Ответ: Н₀ отклоняется. Принимается Н₁. Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, неслучайны (р=0,0039).

Задача 3. Изучался уровень ориентации учащихся на художественно-эстетические ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились беседы, выставки детских рисунков, были организованы посещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. С целью проверки эффективности этой работы до начала эксперимента и после давался тест. Результаты тестирования приведены в таблице.

Время	ИСПЫТУЕМЫЕ
	1	2	3	4	5	6	7	8	9	10	11	12
	БАЛЛЫ
до	16	14	17	18	14	15	16	10	15	19	13	16
после	23	17	22	24	18	15	16	18	22	21	25	21

Решение.

Данные в условии задачи представлены по одной экспериментальной выборке и совершено два замера (до и после) выбирает критерий Т Вилкинсона.

Сформулируем гипотезы.

H₀: Интенсивность положительных сдвигов не превосходит интенсивности отрицательных сдвигов.

H₁: Интенсивность положительных сдвигов превосходит интенсивность отрицательных сдвигов.

1. Находим разности парных вариант и помещаем их в таблицу 1.

2. Определяем ранги полученных разностей (без учета знаков, пары наблюдений, разности которых оказались равными нулю, из дальнейшей оценки исключаются).

3. Поскольку отрицательных сдвигов меньше, определяем сумму их рангов: 1 + 2 + 3,5 = 6,5

4. Устанавливаем достоверность различий. При количестве наблюдений меньше 26 сравнивают найденную сумму с максимальными значениями Т, при которых различия еще могут считаться достоверными (Приложение 3).

Табл. 1

Время	ИСПЫТУЕМЫЕ
	1	2	3	4	5	6	7	8	9	10	11	12
	БАЛЛЫ
до	16	14	17	18	14	15	16	10	15	19	13	16
после	23	17	22	24	18	15	16	18	22	21	25	21
Разности	7	-1	5	6	4	0	0	-2	7	-4	12	5
Ранги	8,5	1	5,5	7	3,5			2	10	3,5	8,5	5,5

Для n = 10 имеем

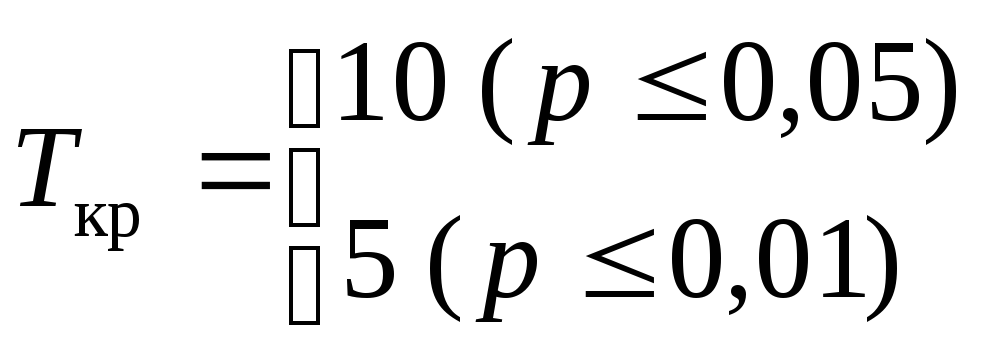
Так как Т_эмп < Т_кр гипотеза H₀ отклоняется. Принимается гипотеза H₁.

Ответ. Преобладание положительных сдвигов не случайно (p < 0,05). Беседы, выставки детских рисунков, посещения музеев и картинных галерей, встречи с музыкантами, художниками и др. дали положительные результаты.

Задача 4. Три группы испытуемых (опытные операторы-профессионалы, операторы-новички и студенты, не имевшие опыта операторской работы) выполняли задачу по слежению за движущимся объектом. По 10 опытам, проведенным с каждым испытуемым, было рассчитано среднее количество ошибок. Определите, зависит ли число ошибок от профессионального опыта испытуемых? Какие группы испытуемых значимо отличаются друг от друга по числу ошибок?

Решение. Сформулируем гипотезы.

Н₀: Различие в числе ошибок, сделанных различными группами, являются не более выраженными, чем различия, обусловленными случайными причинами.

Н₁: Различие в числе ошибок, сделанных различными группами, являются более выраженными, чем различия, обусловленными случайными причинами.

	Опытные операторы	Операторы-новички	Студенты
1	3.13	1.39	5.47
2	3.25	5.38	5.60
3	3.64	4.07	6.88
4	3.40	3.87	6.40
5	2.59	4.37	3.02
6	1.97	3.79	6.18
7	3.16	3.33	5.52
8	4.22	5.39	4.15
9	1.36	3.37	2.07
10	3.47	4.74	4.68
суммы	30.19	39.70	49.97	119.860
средние	3.019	3.970	4.997

1. Подсчитаем SS_факт - вариативность признака, обусловленную действием исследуемого фактора.

где Т_с – сумма индивидуальных значений по каждому из условий.

с – количество условий (градаций) фактора (=3);

n – количество испытуемых в каждой группе (= 10);

N – общее количество индивидуальных значений (= 30);

–квадрат общей суммы индивидуальных значений.

2. Подсчитаем SS_общ – общую вариативность признака:

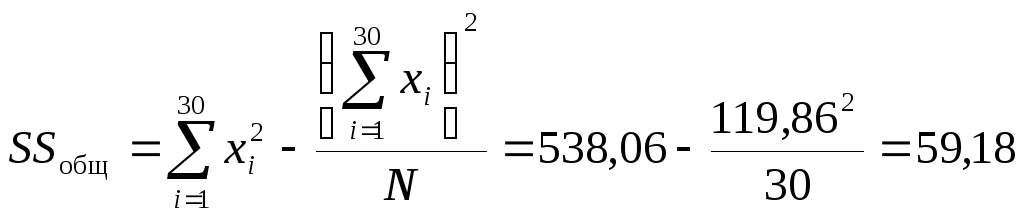
3. Подсчитаем случайную (остаточную) величину SS_случ, обусловленную неучтенными факторами:

SS_случ = SS_общ – SS_факт = 59,18 – 19,57 = 39,60

4. Число степеней свободы равно:

k_факт = k₁ = c – 1 = 2

k_общ = N – 1 = 29

k_случ = k₂ = k_общ – k_факт = 29 – 2 = 27

5. Математическое ожидание суммы квадратов (усредненная величина соответствующих сумм квадратов SS) равно:

6.Значение статистики критерия F_эмп рассчитаем по формуле:

7. Определим F_крит по таблице Приложения 6. Для k₁=2 и k₂=27 табличное значение статистики равно F_крит = 3,35

8. Для нашего примера F_эмп > F_крит (6.67 > 3.68), следовательно принимается гипотеза Н₁.

Ответ: Различие в числе ошибок, сделанных различными группами, являются более выраженными, чем различия, обусловленными случайными причинами.

Задача 5: Провести классификацию пяти испытуемых, характеризующихся по следующим показателям: x₁ , x₂ , x₃ , x₄

Таблица основных показателей

№ предприятия	x1	x2	x3	x4
1	3.338	78.46	5.013	7.312
2	1.090	50.83	3.423	17.785
3	6.653	26.12	3.314	21.544
4	2.105	72.11	2.534	8.125
5	6.178	13.70	1.863	1.780

1. Средние значения показателей и их средние квадратические отклонения равны:

s₁=2,0088; s₂=25,1875; s₃= 1,0561; s₄= 7,2610.

2) Рассчитаем матрицу нормированных исходных данных:

.

3) Зададим «веса» по степени важности показателя: w₁=0,4; w₂=0,3; w₃=0,2; w₄=0,1

4) Вычислим матрицу расстояний (в силу симметрии матрицы ограничимся записью только наддиагональных элементов):

.

5) Из матрицы R₁ следует, что наиболее близкими являются объекты 2 и 4 (_2,4=0,78), и поэтому они объединяются в один кластер. После объединения имеем четыре кластера:

1 → 1^'

2,4 → 2^'

3 → 3^'

5 → 4^'

Расстояния между новыми кластерами будем находить по принципу «ближайшего соседа». Так за расстояние между кластерами 1 и 2 берется наименьшее из двух расстояний ; между кластерами 2 и 3 - ; между кластерами 2 и 4 - . остальные расстояния остаются без изменения.

6) получим матрицу расстояний после первого шага кластеризации:

7) Из матрицы R следует, что наиболее близки кластеры 3 и 4 () и, следовательно, они объединяют в один кластер. После второго объединения будем иметь три кластера:

1^' → 1^''

2' → 2^''

3',4' → 3^''

Расстояния между новыми кластерами будут следующие:

_1”2”=1,13 (останется без изменения); _1'',3''=min{_1'2';_1',4'}= =min{1,93;2,30}=1,93 и _2''3''=min{_2',3'; p_2',4'}=min{1,63; 1,90}=1,63.

8) Получим матрицу расстояний после второго шага кластеризации:

.

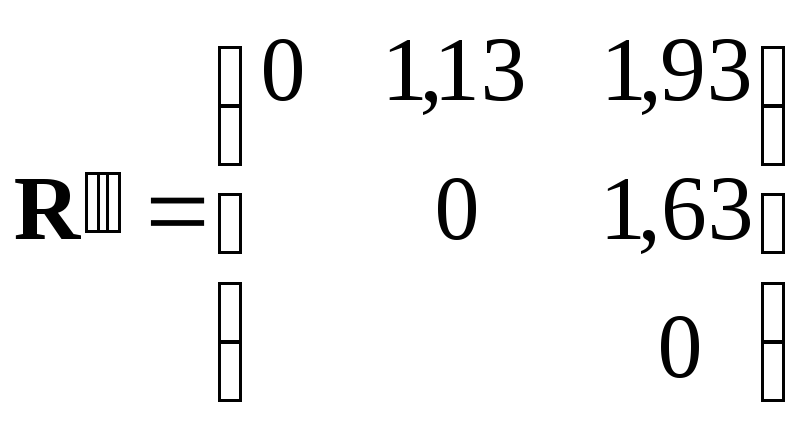9) Минимальное расстояние между кластерами 1^'' и 2^'' (_1'',2''=1,13), следовательно, эти кластеры объединяют в один кластер:

1, 2 → 1

3 → 2

Расстояние между новыми кластерами будет равно _1'''2'''=min{p_3''1''; p_3''2''}= =min{1,93; 1,63}=1,63.

10) Тогда получим матрицу расстояний:

.

Таким образом, на расстоянии =1.63 два кластера объединяются в один.

11) Результаты иерархической классификации наблюдений представляются в виде денрограммы, в которой по оси ординат приводятся расстояния между объединенными на данном этапе кластерами:


				1,63					5 этап
									4 этап
		1,13							3 этап
						1,11
									2 этап
				0,78
									1 этап

1 2 3 4 5 Номер кластера

Вывод: Предпочтение следует отдать предпоследнему этажу кластеризации, т.е. все испытуемые по данным показателям объединяются в два кластера: (1, 2, 4) и (3, 5).

Задача6. На основании данных по трем показателям: X₁; X₂ и X₃ испытуемые были разделены на две группы X и Y. Можно ли испытуемого Z отнести к группе X?

Таблица исходных данных

Группы испытуемых	X1	X2	X3
X	224,228 151,827 147,313 152,253	17,115 14,904 13,627 10,545	27,981 21,481 28,669 10,199
Y	46,757 29,033 52,134 37,050 63,979	4,428 5,510 4,214 5,527 4,211	11,124 6,091 11,842 11,873 12,860
Z	55,451	9,592	12,840

Решение:

Запишем исходные данные для испытуемых группы (X) и для испытуемых группы (Y) в виде матриц:

,

Находим векторы средних значений:

;

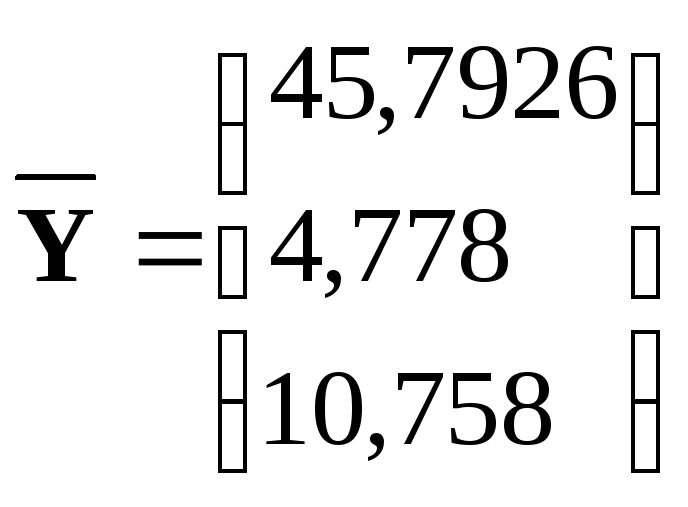
Составим вспомогательные матрицы:

,

Вычисляем ковариационные матрицы по формулам и:

,

Вычисляем вектор разности средних значений:

Несмещенная оценка суммарной ковариационной матрицы равна:

Вычисляем обратную матрицу для суммарной ковариационной матрицы:

Умножив полученную обратную матрицу на вектор разности средних, получим вектор оценок коэффициентов дискриминантной функции:

Умножив исходные матрицы X и Y на вектор a, получим оценки дискриминантной функции для этих матриц:

,

Далее рассчитываем средние значения оценок дискриминантных функций исходных матриц X и Y по формулам:

и константу дискриминации

В заключение, определим значение показателя для дискриминации испытуемого Z:

U_z=a_1zz₁+a₂z₂+a₂z₃=55,4510,1045+9,5922,0478+12,840(-0,13645)=23,686.

Вывод: Так как U_z<C, поэтому данного испытуемого нельзя отнести к группе X.

Задача 7. В результате некоторого эксперимента получены следующие результаты: 11, 13, 12, 9, 10, 11, 8, 10, 15, 14, 8, 7, 10, 10, 5, 8. Необходимо проверить нормальность распределения результативного признака.

Вычисляем и.

1) интервалx±3S [10,06 – 7,86; 10,06 + 7,86] или [2,20; 17,92]. В этот интервал попадают все значения.

2) интервал x±S [10,06-2,62; 10,06+2,62] или [7,42; 12,68]. В этот интервал попадают 11 значений, что составляет 11/16 = 0,7 от объема выборки.

3) 0,657 S =0,657 · 2,62 = 1,72

интервал или x±0,657S [10,06-1,72; 10,06+1,72] или [8,34; 11,78]. В этот интервал попадают 7 значений, что составляет около 50 % от объема выборки.

4)

Распределение данного признака не отличается от нормального.

5)

,

что также свидетельствует о нормальности распределения признака.

6) рассчитаем критическое значение коэффициента асимметрии по формуле:

7) рассчитаем критическое значение коэффициента эксцесса по формуле:

Так как A_эмп < A_кр и E_эмп < E_кр, то распределение результативного признака не отличается от нормального.

8) Дополнительные проверки на нормальность эмпирического распределения основаны на критериях ² Пирсона и λ Колмогорова-Смирнова.

Задача 8. Построить гистограмму.

Дана выборка: 17, 12, 15, 14, 17, 13, 16, 14, 19, 20, 15, 17, 18, 16, 17, 18, 11, 21, 17, 17.

Объем выборки n=20. x_min=11, x_max=21. Размах выборки =21-11=10. Число классов K=1+3.32lg20=5.32. Величина частичного интервала равна x=/K=10/5.32=1.88.

Границы частичных интервалов равны x_1н=x_min-x/2=11-0.94=10.06; x_1в=x_2н=x_min+x/2=11+0.94=11.9. x_2в=11,94+1,88=13,82; x_3в=13,82+1,88=15,70; x_4в=15,70+1,88=17,58; x_5в=15,70+1,88=19,46; x_6в=19,46+1,88=21,34.

Строим таблицу:

Частичные интервалы	[10.06; 11.94)	[11.94; 13.82)	[13.82; 15.70)	[15.70; 17.58)	[17.58; 19.46)	[19.46; 21.34)
mi	1	2	4	8	3	2
mi/(x∙n)	0.0266	0.053	0.106	0.212	0.080	0.053

Для построения гистограммы относительных частот необходимо правильно выбрать масштабы и начало отсчета. Так по вертикальной оси плотность изменяется от 0 до 0,25 с шагом 0.05, а по горизонтали - от 10 до 22 с шагом 2. Построение гистограммы осуществляется на миллиметровой бумаге с соответствующей точностью.