Integration by Parts

Theorem 2. Let u (x) and v(x) defined and differentiable on the interval X and u '(x) v (x) is primitive in this interval. Then the function u (x) v '(x) is also primitive in the interval X, and the formula

Given the differential function of the form v'(x)dx = dv and u' (x) dx = du (6.2) is often used in the form

Equality (6.2) (or (6.3)) is the formula of integration by parts.

Consider the examples of finding integrals by integration by parts.

Example 4. dx.

DECISION. Here we take и(х) = ln x, dv = dx, i.e v = х. By (6.2) yields

9- lecture

Definite integral. Basic properties. The basic formula of integral calculus. Basic rules of integration. Applying of integrals in economy.

Let the function f (x) is defined on the interval [a, b]. Divide the interval [a, b] into n arbitrary parts of points:

We choose in each of the partial segments [x_i, x_i+1] arbitrary point ξ_i :

Now we form the sum of the products:

which will be called the integral sum of the function f (x) on [a, b]. The geometric meaning of the value of σ are shown in Fig. 7.1: This is the sum of areas of rectangles with bases Δx_i and height f(ξ_i) (i = 1, 2, ..., n).

Introduce another value. We denote the length of λ maximum daily length of the partition:

Definition. Finite limit I of integral sum σ when λ → 0, if it exists, is called the definite integral of the function f (x) over the segment [a, b]:

The definite integral is denoted

If the definite integral (7.2) exists, then the function f (x) is called integrable on [a, b], the numbers a and b - the lower and upper integration limits, f (x) – integrand, x - variable of integration.

The definite integral is independent of the symbol variable of integration, i.e.

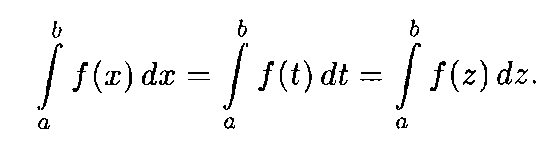
Classes of integrable functions

The answer to the question of what functions are integrable (ie, there is a definite integral (7.2)), give the following theorem, which we give without proof.

Theorem 1. If the function f (x) is continuous on [a, b], then it is integrable on it.

Theorem 2. If defined and bounded on the interval [a, b] the function f (x) has a finite number of points of discontinuity, then it is integrable on this interval.

Theorem 3. Monotone on [a, b] the function f (x) is integrable on this interval.

The basic properties of the definite integral

Integral has been defined for the case where a <b. We generalize the concept of a definite integral and on other occasions.

By definition we

as the definite integral on the segment of length zero.

Also, by definition, assume that

because when driving on b to the a length of all partial segments Δxi = xi-1 - xi have a negative sign in the integral sum (7.1).

2. For any numbers a, b and c have the equality

3. A constant factor can be taken outside the sign of the definite integral:

4. The definite integral by the integral of an algebraic sum of functions is the algebraic sum of definite integrals:

5. If the function f (x) ≥ 0 everywhere on [a, b], then

6. If f (x) ≤ g (x) everywhere on [a, b], then