Gradient
Consider the function of three variables, and = f (x, y, z), differentiable at a point M (x, y, z).
Definition 1. The gradient of and = f (x, y, z) is a vector whose coordinates are, respectively, the partial derivatives at the point M.
To indicate the gradient of the function used is character
Similarly, in the case of a function of two variables f = (x, y), we have
Gradient function characterizes the direction and magnitude of the maximum rate of increase of the function at the point.
To determine the geometric meaning of the gradient of introducing the concept of surface level.
Definition 2. Level surfaces of functions u = f (x, y, z) is a surface on which the function is constant
Example .
Find gradient and module function
at z = M (0, 1).
DECISION. According to the formula (8.8) we have for the function of two variables
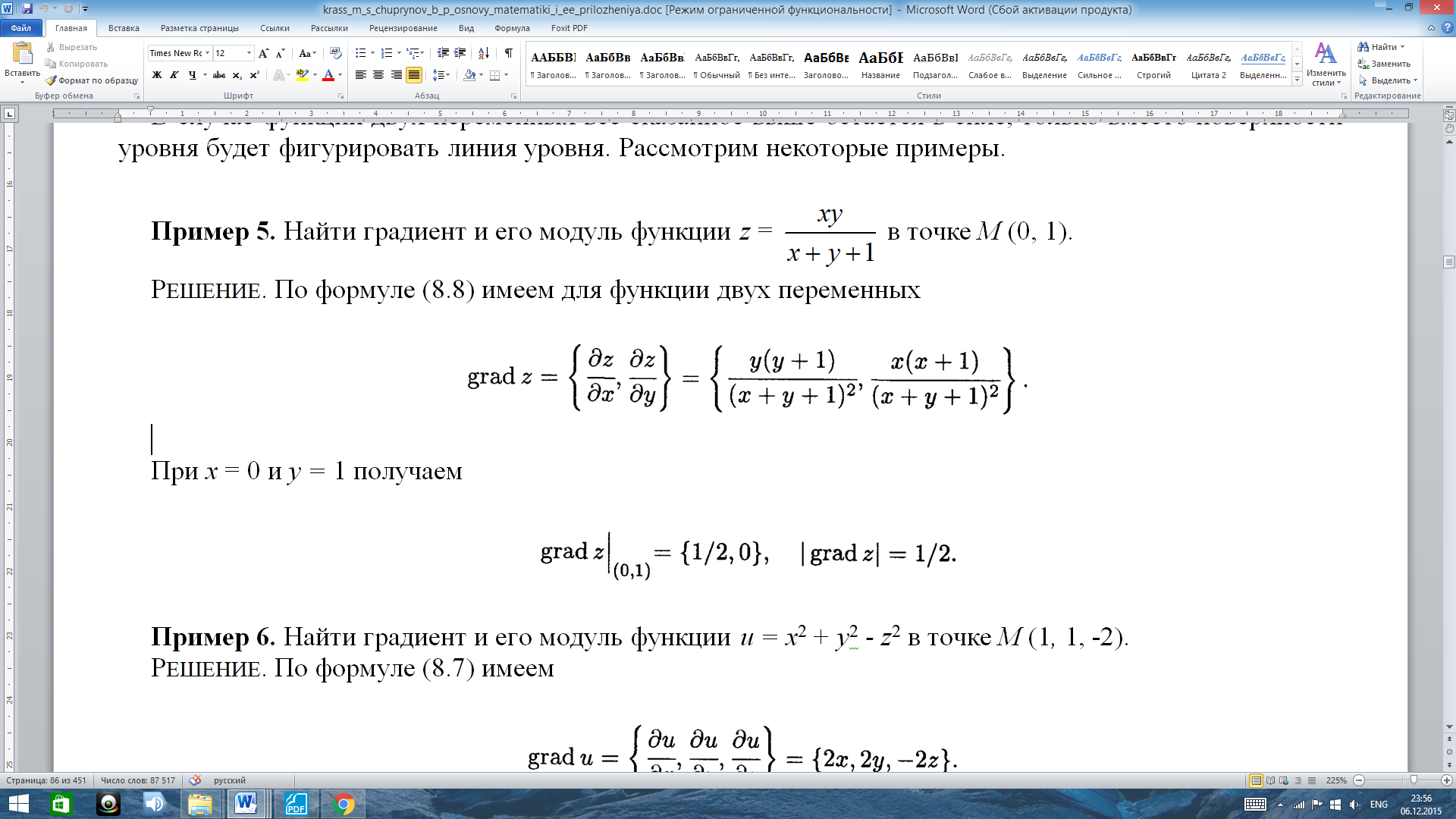
When x = 0 and y = 1 we obtain
8- lecture
Indefinite integral. Basic properties. Table of basic indefinite integrals. The concept of primitive function
Previous lecture we considered the main problem of differential calculus - finding the derivative of a given function. Many questions of mathematical analysis and applications in a variety of science leads to another problem: for a given function f (x) to find a function F (x), the derivative is equal to the function f (x).
Definition 1. The function F (x) is called primitive for the function f (x) on the interval X, if for any x X function F (x) is differentiable and the equality F '(x) = f (x).
Here are some examples.
Example 1.
The function F (x) = sinx is a primitive for the function f (x) = cos
x on the infinite interval (-
, +
) since for any x the equality (sin x) '= cos x.
Example 2.
The function F (x) = ln x - primitive function f (x) = 1 / x in the
interval (0, +
)
because each point of this range, the equality (ln x) '= 1 / x.
Note that the problem of finding the given function f (x) its primitive ambiguous; if F (x) - primitive, then the function F (x) + C, where C - arbitrary constant number, and primitive function f (x), as the [F (x) + C] '= f (x) .
The indefinite integral
Definition 2. The set of all primitive functions for function f (x) on the interval X is called the indefinite integral of the function f (x) on this interval and is denoted by
In
this notation
is
called the integral sign (this stylized latin letters S, meaning the
sum),f(x)
- integrand function,
f(x)dx
- integrand, and the variable x - variable of integration.
The operation of finding the primitive of its derivative or indefinite integral of a given integrand is called integration of this function. Integration is the inverse operation of differentiation. To check the correctness of the integration result to differentiate and get the integrand.
Consider some examples.
Example
3.
=x2
+ С
check: (x2
+ С)'
= 2х.
Example
4.
= - cos
х + С;
check:
(-cos
х
+ С)'
= sin
x.
Example
5.
=
е3x
+ С;
check: (
+C)'
=
е3x.
Basic properties of the indefinite integral
The following two properties are called linear properties of the indefinite integral.
Table of basic indefinite integrals
Basic methods of integration
Direct integration
Calculation of integrals using the basic properties of indefinite integrals and integrals simple table called direct integration. We show this by example.
Example 1.
Example2.
Method of substitution
Replacing the variable of integration is one of the most effective methods of information of the indefinite integral to the table. This is called the substitution method, or by replacing the variable. It is based on the following theorem.
Theorem 1. Suppose that х = φ(t) is defined and differentiable on an interval Т , and Х - the set of values of this function, which defines a function f(x). If the function f(x) has a primitive on the set Х , then the set Т the formula
Expression (6.1) is called a change of variables formula in the indefinite integral. Consider the application of this method on the examples of calculation of integrals.
Example 3.
.
DECISION. Here expansion in binomu Newton is very difficult. We introduce a new variable t = х — 1. Then х = t + 1, dx = dt, and the original integral is transformed as follows:
To make the reverse change of variable to get a definitive answer:
