1- lecture

Vector space. The linear dependence of vectors. Decomposition of the vector on the basis.

Vectors

Meaning, geometric representation, and types of vectors

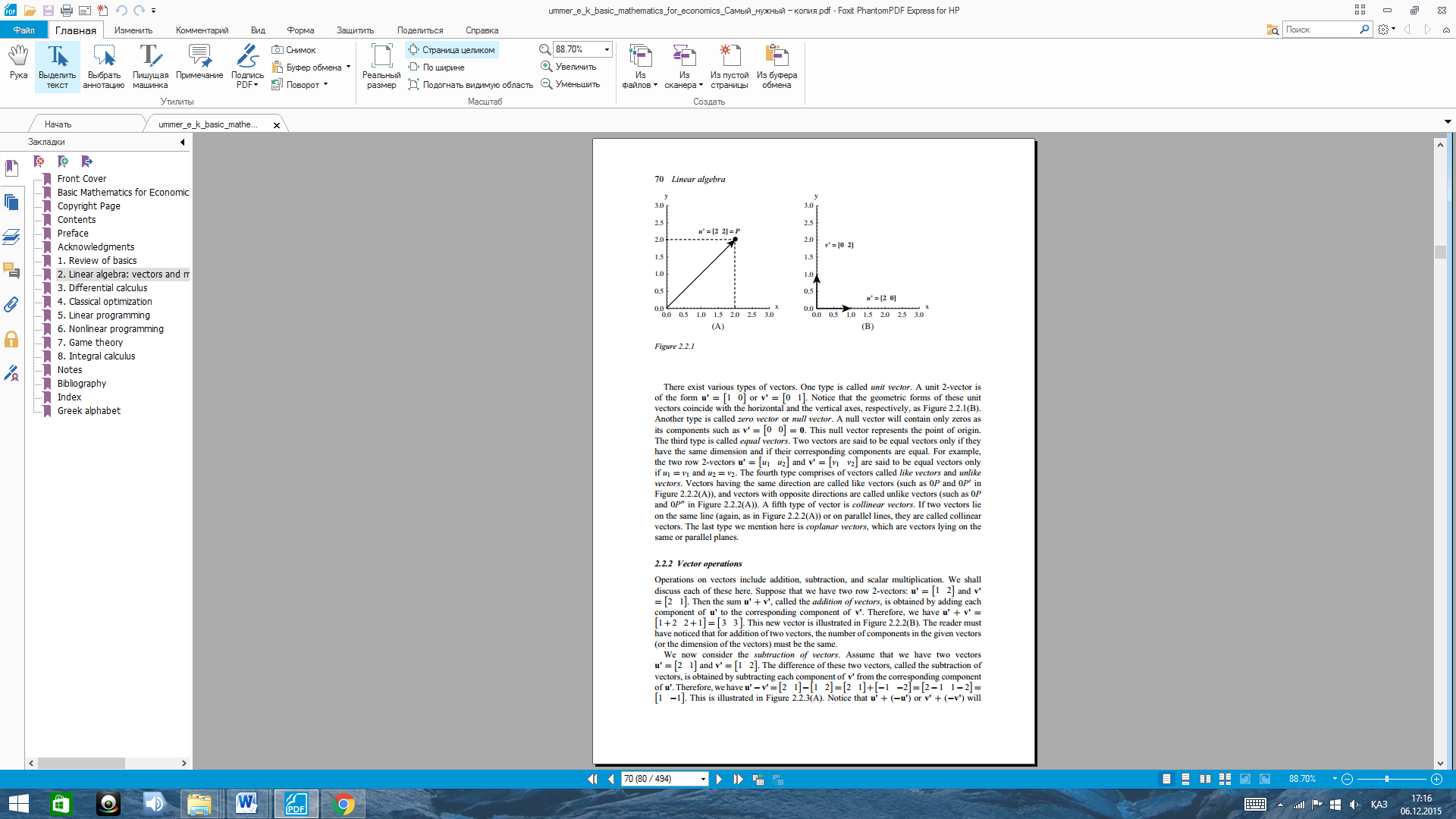
Vector operations

2- lecture

Matrices and operations on matrices. Determinants. Basic properties. Rank of the matrix.

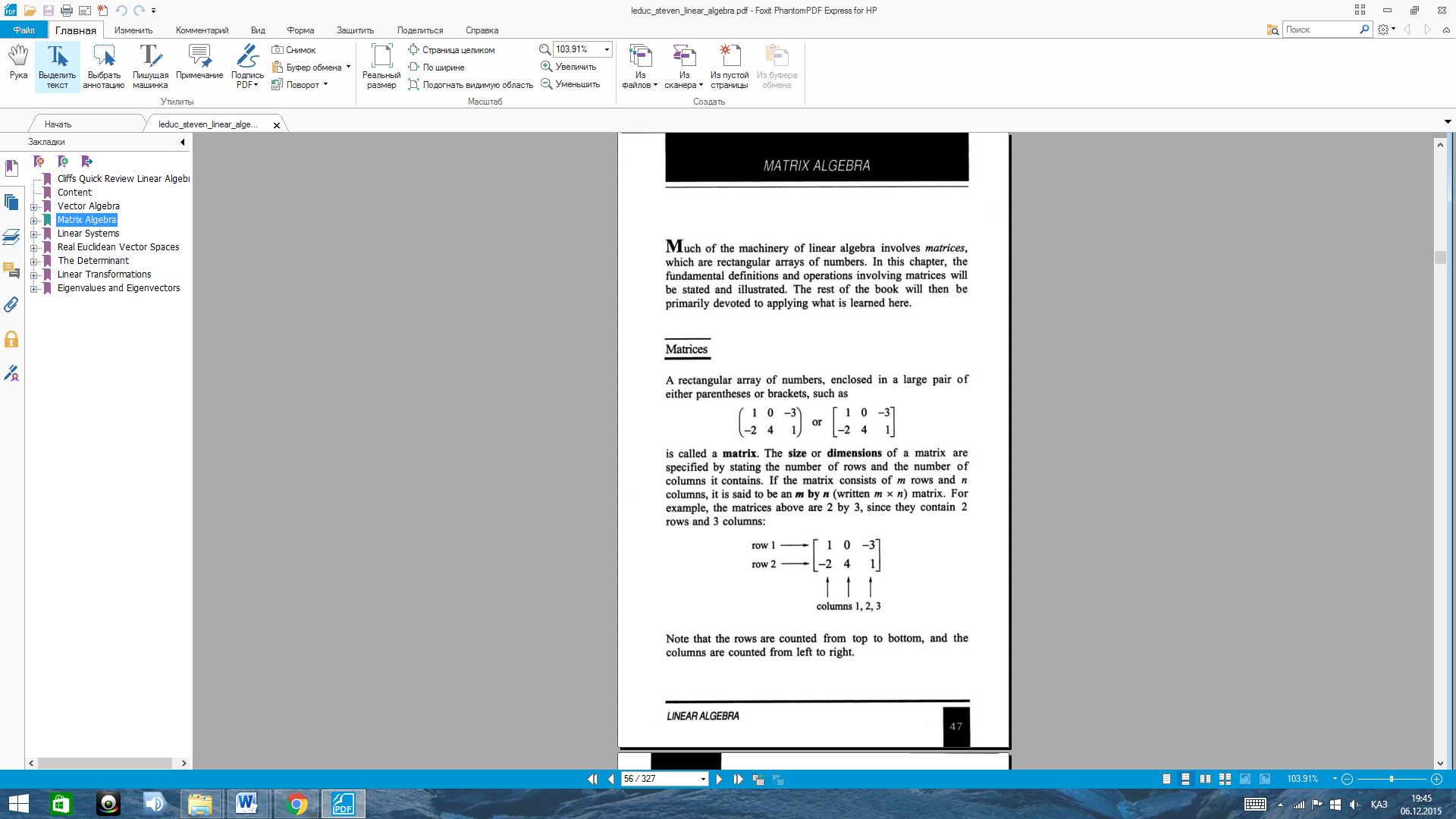
Two of the importantproperties of scalar multiplicationof matrices are the following.

3- lecture

System of linear algebraic equations and methods for their solutions (Formula Cramer, Gauss methods).

4- lecture

The use of elements of linear algebra in the economy. Leontief model of a diversified economy.

Macroeconomics operation of a diversified economy requires a balance between the different branches. Each sector on the one hand, is prizvoditelem, and on the other - the consumer products produced by other industries. There is quite a difficult task of calculating the relationship between the branches through the production and consumption of products of different types. This problem was first formulated in the form of a mathematical model in 1936 in the writings of well-known American economist Leontief, who tried to analyze the causes of the economic depression of the United States 1929-1932. This model is based on matrix algebra and matrix analysis using the device.

Balance sheet ratio

For simplicity, we assume that the manufacturing economy is a sphere n branches, each of which produces a homogeneous product. To secure its production every industry needs from other sectors (industrial consumption). Typically the process of production is considered for a certain period of time; in some cases, such a unit is the year.

We introduce the following notation:

x_i - total output of i-th branch (its gross output);

the volume of product i-th industry consumed j-th industry in the production volume

of products xj;

the volume of product i-th branch, intended for sale (consumption) in the non-manufacturing

sector, or the so-called end-use product. This includes personal consumption of the citizens,

satisfaction of social needs, the content of the state institutions, etc.

The balance principle of communication in various industries is that the gross output of the i-th sector should be equal to the sum of consumption volumes in the industrial and non-industrial sectors. In its simplest form (the hypothesis of linearity, or simple addition) balance relations are of the form

This equation (16.2) is called the balance of relations.

Since the products of different industries have different dimensions, we will in the future to keep in mind the value balance.

The linear model of a diversified economy

Leontief based on an analysis of the US economy and the period before World War II was installed is an important fact: in the long-term value of change very little and can be considered as constants. This phenomenon is understandable in light of the fact that production technology remains at the same level for quite some time, and, therefore, consumption of the j-th branch of production i-th industry in the production of its product volume xj have the technological constant.

In view of this fact, you can make the following assumption: production for the j-th industry volume xj need to use the products of the i-th industry volume aijxi, where aij - constant. With this assumption, the linear production technology is adopted, and this very assumption is called the hypothesis of linearity. At the same time the number of coefficients Aij are called direct costs. According to the hypothesis of linearity, we have

Then equation (16.2) can be rewritten as a system of equations

We introduce the column vectors of the volume of output (gross output vector), the volume of production of final consumption (final consumption vector) and the matrix of coefficients of direct costs:

Then the system (16.4) in matrix form is

Typically, this ratio is called the equation of linear input-output balance. Together with the description of the matrix representation (16.5) this equation is called the Leontief model.

Interbranch balance equation can be used for two purposes. In the first, the most simple case, when the known vector of gross output , required to calculate the vectorof final consumption and, and - a similar problem was discussed above (n. 16.1, Example 5).

In the second case, the equation of interbranch balance is used for planning purposes, the following formulation of the problem: for the time period T (for example, one year) known vector of final consumption and want to define the vector's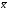gross output. It is necessary to solve a system of linear equations (16.6) with a known matrix A and the target vector. In the future we will deal precisely with such a task.

Meanwhile, the system (16.6) has a number of peculiarities arising from the applied nature of this problem; first of all, all the elements of the matrix A and the vectors 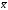and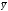must be non-negative.

5- lecture