
матем / Mathematics in economics
.docx|
1 |
1 |
1 |
Vectors. Meaning, geometric representation, and types of vectors. |
|
1 |
1 |
2 |
Operations on vectors. Addition and scalar multiplication. |
|
1 |
1 |
3 |
The properties of vector addition and scalar multiplication. |
|
1 |
1 |
4 |
Linear combination of vectors. |
|
1 |
1 |
5 |
Linear dependence of vectors and linear independence of vectors. |
|
1 |
1 |
6 |
Scalar product of vectors and its properties. |
|
1 |
1 |
7 |
Vector spaces. One-dimensional and two- dimensional vector space. |
|
1 |
2 |
1 |
Let u=[1, 3, 5] and v=[2, 4 ,6]. Find the following:
|
|
1 |
2 |
2 |
Let u=[1, 3] and v =[2, 4]. Find, and illustrate, the following:
|
|
1 |
2 |
3 |
Find the scalar products of the following vectors: u=[5, 15, 25] and v =[1, 3, 5]. |
|
1 |
2 |
4 |
Find the domain of the following functions:
|
|
1 |
2 |
5 |
Let
Which of these matrices are conformable for addition and subtraction? Find the sums and differences of those matrices that are conformable for addition and subtraction. |
|
1 |
2 |
6 |
Use
the sum-or-difference and power rules to find
|
|
1 |
2 |
7 |
Find
the following indefinite integrals:
|
|
1 |
3 |
1 |
Solve the following SSLEs using the Gauss method:
|
|
1 |
3 |
2 |
Let
|
|
1 |
3 |
3 |
Find the limit, if it exist, of the following function:
|
|
1 |
3 |
4 |
Find
the following indefinite integral:
|
|
1 |
3 |
5 |
Solve the following LP problem: maximize П=4x+3y, subject to 2x+4y≤40, 4x+2y≤50, 2x+2y≤40, and x,y≥0. |
|
1 |
3 |
6 |
Evaluate
the following definite integral:
|
|
2 |
1 |
1 |
Matrices. Types of matrices. |
|
2 |
1 |
2 |
Matrix operation: scalar multiplication, addition and subtraction. |
|
2 |
1 |
3 |
Matrix operation: multiplication. The properties of matrix multiplication |
|
2 |
1 |
4 |
Transpose of a matrix. Symmetric matrix. Properties of matrix transposition. |
|
2 |
1 |
5 |
The system of linear algebraic equations and solution methods. Formula Cramer. |
|
2 |
1 |
6 |
Gauss method and its characteristics. |
|
2 |
1 |
7 |
Functions. Univariate functions. |
|
2 |
2 |
1 |
Types of functions and their graphs. |
|
2 |
2 |
2 |
Find the scalar products of the following vectors: u=[5, -3, 2] and v =[-1, 2, 4]. |
|
2 |
2 |
3 |
Find the transpose of the following matrice:
|
|
2 |
2 |
4 |
Find the limit, if it exist, of the following function:
|
|
2 |
2 |
5 |
Let
|
|
2 |
2 |
6 |
Find
partial derivatives
|
|
2 |
2 |
7 |
Solve the following LP problems: Minimize C=3x+2y, subject to x+10y≥20, 10x+y≥40, and x,y≥0 |
|
2 |
3 |
1 |
Calculate the indefinite integral by substitution methods:
|
|
2 |
3 |
2 |
Find the initial support solution to the transportation problem by northwestern methods.
|
|
2 |
3 |
3 |
Let
|
|
2 |
3 |
4 |
Let
|
|
2 |
3 |
5 |
Find
the following indefinite integrals:
|
|
2 |
3 |
6 |
|
|
3 |
1 |
1 |
Limit of functions. Properties of limits. |
|
3 |
1 |
2 |
Continuity function. Properties of continuity. |
|
3 |
1 |
3 |
Derivatives of univariate functions and notations. |
|
3 |
1 |
4 |
Rules of differentiation of univariate functions. |
|
3 |
1 |
5 |
Indefinite integrals. Integration as anti-differentiation. Notations and concepts. |
|
3 |
1 |
6 |
Rules of integration. Integration by parts. |
|
3 |
1 |
7 |
Definite or Riemann integrals. Notations and concept. |
|
3 |
2 |
1 |
Fundamental theorem of integral calculus. Newton –Leibniz formula. |
|
3 |
2 |
2 |
|
|
3 |
2 |
3 |
Find the transpose of the following matrice:
|
|
3 |
2 |
4 |
Suppose
that we have an equation of matrices given by 4A−2B=C.
Let
|
|
3 |
2 |
5 |
Find
the derivative of a composite function
|
|
3 |
2 |
6 |
Find
the limit of the function by using the second
remarkable limit:
|
|
3 |
2 |
7 |
Find
the gradient and its modulus of the function at said point:
|
|
3 |
3 |
1 |
Calculate the integral by the method integration by parts:
|
|
3 |
3 |
2 |
Find
the limit of the function by using the first remarkable limit:
|
|
3 |
3 |
3 |
Find
the initial support solution to the transportation problem by
minimum tariff.
|
|
3 |
3 |
4 |
Find
the derivative of a composite function:
|
|
3 |
3 |
5 |
Find the solution of a system of linear equations by Gauss methods:
|
|
3 |
3 |
6 |
Let
|


 .
. given
given



 . Calculate the determinant of this matrix using the expansion of
the elements of the thrid columns.
. Calculate the determinant of this matrix using the expansion of
the elements of the thrid columns. .
.
 .
. .
. .
. Find
Find

 of function
of function
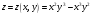 .
.

 .
Find the product of this matrices: AB=?
.
Find the product of this matrices: AB=? .
Calculate
the determinant of this matrix using the expansion of the elements
of the fourth row.
.
Calculate
the determinant of this matrix using the expansion of the elements
of the fourth row.
 .
.
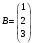 .
. .
Find
C.
.
Find
C.
 .
. .
.
 .
. .
.


 .
Find the minor
.
Find the minor
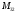 and cofactor
and cofactor
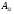 of the element
of the element
 of the matrix
of the matrix
 .
.