
ДРТЦ дляЗАО / Лекция №10
.docЛекция №10
Тема: Фильтры Баттерворта
Учебные вопросы
1 Постановка задачи синтеза ФНЧ. Определение фильтра Баттерворта.
2 Определение комплексной передаточной функции ФНЧ.
3 Определение структуры и параметров ФНЧ.
Литература: [2] с.280-284.
1 Постановка задачи синтеза ФНЧ. Определение фильтра Баттерворта.
Наиболее распространенной является задача синтеза фильтров, имеющих АЧХ, удовлетворяющую определенным требованиям.
Актуальной является задача синтеза ФНЧ с АЧХ, наилучшим образом аппроксимирующей АЧХ идеального ФНЧ (см. рис.10.1).

Рис.10.1
Простейшей функцией, пригодной для описания АЧХ синтезируемого фильтра является
![]()
или
![]() (10.1)
(10.1)
где
![]() -
безразмерная нормированная частота,
которой удобно пользоваться при решении
рассматриваемой задачи, n
– целое число, называемое порядком
фильтра.
-
безразмерная нормированная частота,
которой удобно пользоваться при решении
рассматриваемой задачи, n
– целое число, называемое порядком
фильтра.
Фильтр, имеющий АЧХ, удовлетворяющую (10.1) называют фильтром с максимально-плоской характеристикой ил фильтром Баттерворта.
В полосе пропускания фильтра значение АЧХ плавно уменьшается с ростом частоты. При w = wс и значение АЧХ оказывается равным
![]() (10.2)
(10.2)
при любом n.
Причем, чем больше n, тем точнее аппроксимируется АЧХ идеального ФНЧ.
На рис.10.2 показаны графики, построенные по формуле (10.1) для n = 1,2,3,5.

Рис.10.2
Порядок фильтра выбирают, исходя из требований, предъявляемых к ослаблению сигналов с частотами w > wс.
Таким образом, задачу синтеза ФНЧ с заданной АЧХ можно разделить на две составляющие: 1) определение комплексной передаточной функции ФНЧ по выражению для квадрата ее модуля (10.1) с выбранным порядком фильтра n;
2) определение структуры и параметров ФНЧ.
2 Определение комплексной передаточной функции ФНЧ.
Получим комплексную передаточную функцию по выражению для квадрата ее модуля с выбранным n.
Из теории комплексных чисел известно соотношение
![]() (10.3)
(10.3)
С учетом (10.3) выражение (10.1) принимает вид
![]() (10.4)
(10.4)
Для наглядности
дальнейших преобразований положим в
(10.4)![]() и, учитывая, что при этом
и, учитывая, что при этом
![]() , получим
, получим
 (10.5)
(10.5)
поскольку
![]()
Далее определим
нули знаменателя уравнения (10.5), т.е.
корни уравнения
![]() для различных n.
для различных n.
При n = 1 данное уравнение принимает вид 1 – S2 = 0, откуда определяем корни S1 = 1; S2 = -1.
При n = 2 данное уравнение принимает вид
![]() (10.6)
(10.6)
![]()
Откуда получаем четыре корня:
![]()
Эти значения получаются с помощью формулы Эйлера
![]() (10.7)
(10.7)
на основе которой можно записать
![]() (10.8)
(10.8)
Перенеся единицу в (10.6) в правую часть и учитывая (10.8), получаем
![]() (10.9)
(10.9)
Данное уравнение имеет четыре корня, следовательно, K принимает четыре значения: K = 0, 1, 2, 3.
Извлекая корень четвертой степени из левой и правой части (10.9) и придавая K последовательно значения 0, 1, 2, 3, находим корни:

Очевидно, что модули равны единице. Изобразим эти корни на комплексной плоскости. Для n = 1 они приведены на рис.10.3, а для n = 2 – на рис.10.4.
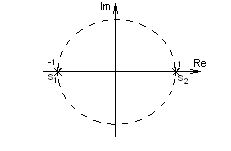

Рис.10.3 Рис.10.4
Таким же образом можно определить корни и для других значений n.
Общая закономерность их расположения на комплексной плоскости характеризуется квадратной симметрией: их число и конфигурация расположения в обеих( левой и правой) полуплоскостях одинаковы.
Зная корни знаменателя выражения (10.5), его можно представить в виде произведения простейших множителей. Например, для n = 1 имеем
![]() (10.10)
(10.10)
для n = 2
![]() (10.11)
(10.11)
Половина корней,
лежащая в левой полуплоскости, принадлежат
передаточной функции
![]() .
Другая половина, лежащая в правой
полуплоскости- функция
.
Другая половина, лежащая в правой
полуплоскости- функция
![]() .
.
Искомой является
передаточная функция
![]() ,
т.к. можно показать, что расположение
корней знаменателя (называемых полюсами
передаточной функции) в левой полуплоскости
соответствует устойчивой цепи.
,
т.к. можно показать, что расположение
корней знаменателя (называемых полюсами
передаточной функции) в левой полуплоскости
соответствует устойчивой цепи.
Следовательно, при n = 1
![]() (10.12)
(10.12)
при n=2
![]() (10.13)
(10.13)
Подставляя значения корней
 в (10.13)
в (10.13)
находим
![]() (10.14)
(10.14)
Рассуждая аналогично, можно найти передаточные функции и для других значений n. Например, при n = 3 передаточная функция фильтра Баттерворта приводится к виду
![]()
Коэффициенты полиномов в знаменателе передаточной функции фильтра Баттерворта приводятся в справочниках по расчету фильтров.
3 Определение структуры и параметров ФНЧ.
Следующим этапом синтеза ФНЧ является реализация найденной передаточной функции фильтра, т.е. определение его приемлемой структуры и значений параметров всех элементов.
Решение задачи реализации ФНЧ неоднозначно и существенно зависит от желательной структуры фильтра и допустимой элементной базы.
Простейшими примерами реализации передаточных функций (10.12) и (10.14) могут служить цепи, изображенные соответственно на рис.10.5 и 10.6.


Рис.10.5 Рис.10.6
Определим комплексные передаточные функции этих цепей.
Для схемы рис.10.5 получаем:
 (10.15)
(10.15)
В формуле (10.12)
делаем подстановку
![]() ,
тогда
,
тогда
 (10.16)
(10.16)
Сравнивая формулы (10.15) и (10.16), заключаем, что частота среза фильтра
![]()
Зная wс, определяемую требованиями на проектирование фильтра можно выбрать параметры R и C.
Для схемы рис.10.6
 (10.17)
(10.17)
Подставляя в
(10.14)
![]() находим
находим
 (10.18)
(10.18)
Сравнивая формулы (10.17) и (10.18), получаем соотношения
![]()
![]()
По известной частоте среза wс можно подбирать параметры элементов R, L и C.
Передаточные функции ФНЧ более высоких порядков можно реализовать, например, каскадным соединением фильтров 1-го и 2-го порядков, отделенных друг от друга идеальными развязывающими элементами (рис.10.7)

Рис.10.7
Под идеальным развязывающим элементом понимают усилитель с коэффициентом усиления K = 1, бесконечно большим входным сопротивлением и выходным сопротивлением, равным нулю.
