2. Условие пропускания реактивного фильтра.

Электрический фильтр является частным случаем четырехполюсника, поэтому для анализа его свойств воспользуемся теорией четырехполюсников.

Основные свойства фильтра определяются его вторичными параметрами: характеристическим сопротивлением и мерой передачиГ.

Примем следующие допущения:

1. будем рассматривать идеальный реактивный фильтр, т.е. фильтр, состоящий из идеализированных реактивных элементов;

2. пусть фильтр является симметричным четырехполюсником, тогда 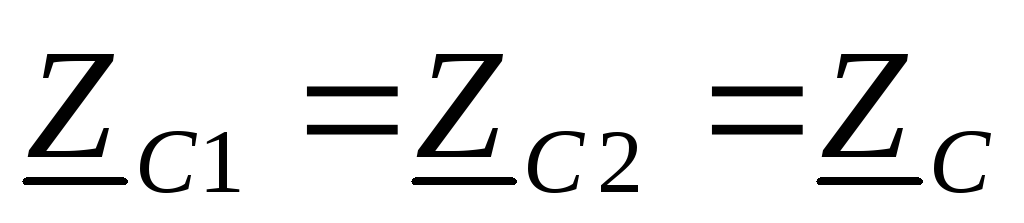и согласно (8.20)

(9.1)

3. пусть фильтр согласован с нагрузкой (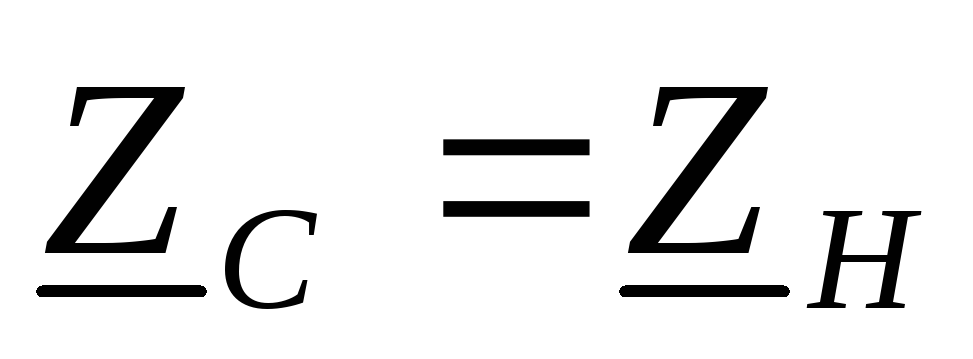), тогда напряжения и токи на входе 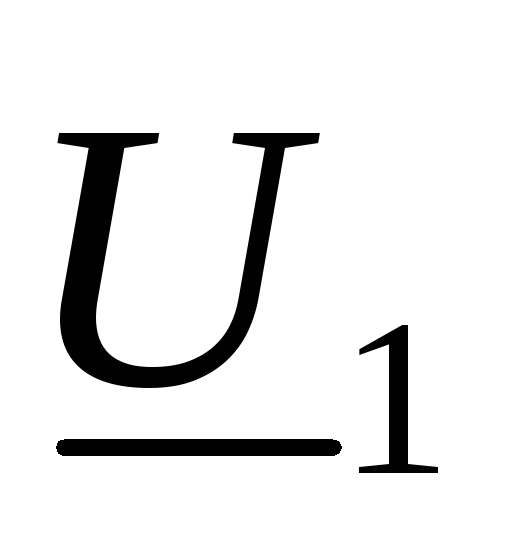, 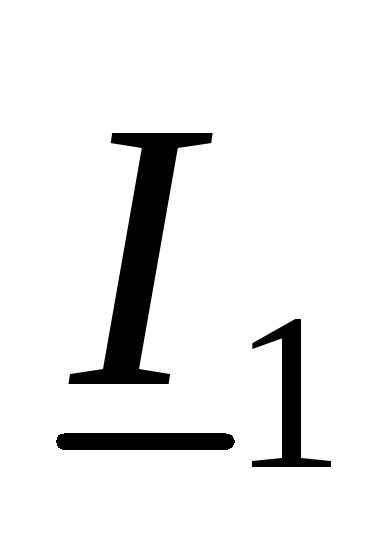и выходе 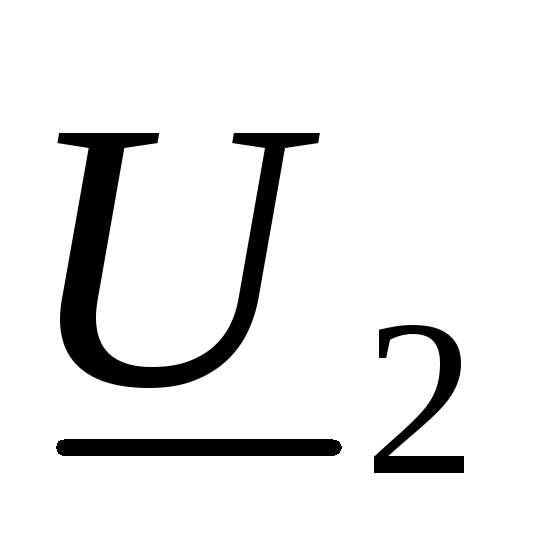, 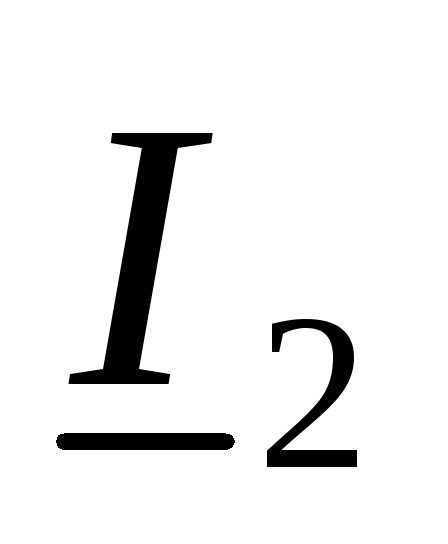связаны известным соотношением:

(9.2)

4. пусть фильтр имеет Т- или П – образную схему замещения, для которых с учетом выражения (7.41) и обозначений, приведенных на рис 9.2, значение параметра А₁₁ имеет вид:

(9.3)

где и – комплексы продольного и поперечного сопротивлений фильтра.

следовательно, с учетом (9.1) и (9.3) получим

(9.4)

Из равенства (9.4) видно, что для определения частотных свойств фильтра необходимо найти величину как функцию частоты.

Для частот, входящих в полосу пропускания, коэффициент затухания равен нулю, т.е. . Следовательно, в этой области выражение (9.4) будет иметь вид:

(9.5)

Поскольку по абсолютному значению не может превышать единицу, то соотношение между сопротивлениямиив пределах полосы пропускания должно удовлетворять условию:

, т.е.

, (9.6)

которое можно преобразовать к виду или

(9.7)

Неравенство (9.7) называется условием пропускания фильтра. Из него следует, что для выполнения условия пропускания, т.е. для обеспечения в определенном диапазоне частот равенства нулю коэффициента ослабления , необходимо, чтобы мнимые составляющие сопротивлений и имели различные знаки или чтобы сопротивления продольной и поперечной ветвей фильтра имели различный характер. Например, если последовательное сопротивление имеет индуктивный характер, то параллельное сопротивление должно иметь емкостной характер (и наоборот).

Четырехполюсник, для которого при всех частотах сопротивления и имеют одинаковый характер (например, индуктивный) не является фильтром, так как он не обладает полосой прозрачности.

Указанное условие еще не является достаточным, необходимо учитывать количественное соотношение между x₁ и x₂.

Таким образом, необходимым и достаточным условием наличия у четырехполюсника полосы пропускания является неодинаковость знаков реактивных сопротивлений продольной x₁ и поперечной x₂ ветвей, а также выполнение неравенства

(9.8)

3. ЧАСТОТЫ СРЕЗА И ПОЛОСА ПРОПУСКАНИЯ РЕАКТИВНОГО ФИЛЬТРА.

Предельные значения частоты, на которых выполняется условие пропускания фильтра (9.7) являются границами полосы пропускания (частотами среза). На этих частотах сопротивления продольной и поперечной ветвей фильтра связаны соотношениями:

;

или

; (9.9)

Таким образом, на одной из частот среза сопротивление продольной ветви фильтра должно быть равно нулю, а на другой сопротивление x₁ продольной ветви должно быть в четыре раза больше, чем сопротивление x₂ поперечной ветви.

Частоты среза находятся из уравнений (9.9) аналитически, если заданы функциональные выражения x₁ и x₂ в зависимости от частоты, или графически, если заданы графики частотных характеристик и.

Анализ выражений (9.1), (9.5) и (9.6) показывает, что в полосе пропускания коэффициент ослабления, а в полосе задерживания Т- и П-образных фильтров коэффициент ослабления определяется выражением:

(9.10)

Таким образом, алгоритм определения вида звена фильтра заданной структуры будет следующим:

1. качественно построить графики функций 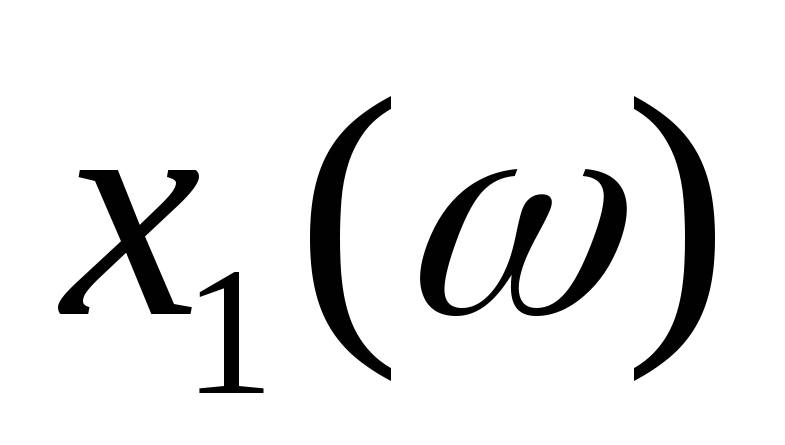,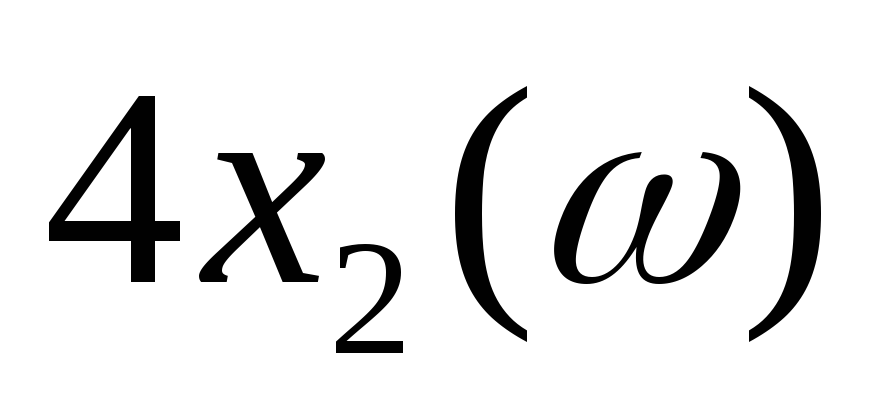и;

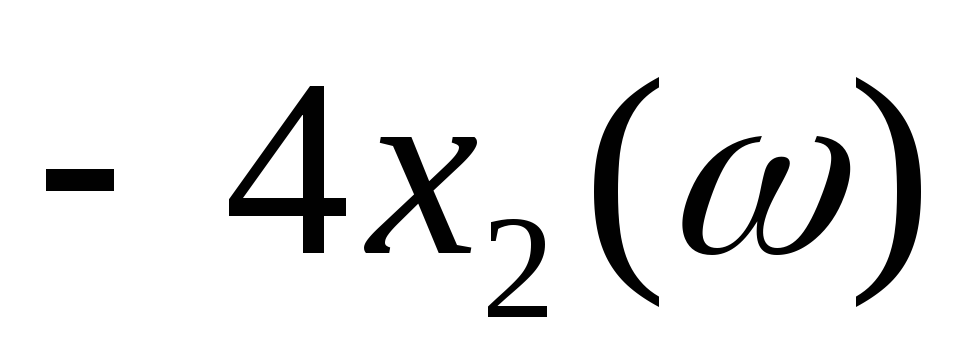2. определить частоты среза согласно (9.9);

3. определить положение полосы пропускания согласно (9.8);

4. построить график 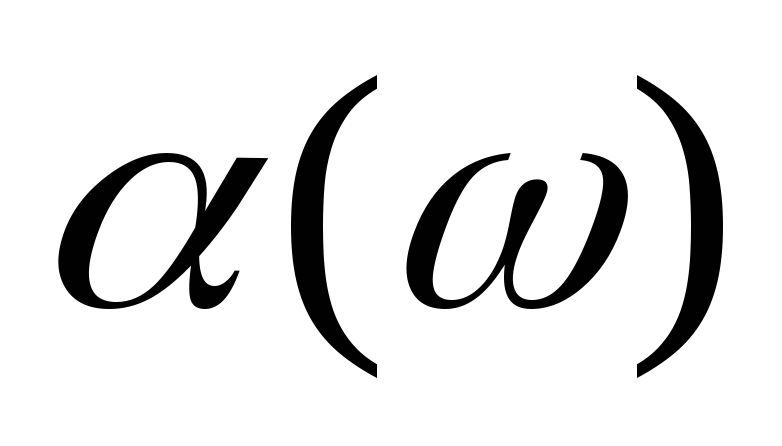и определить по нему вид электрического фильтра.

Пример. Определить вид звена электрического фильтра, схема которого приведена на рис 9.3

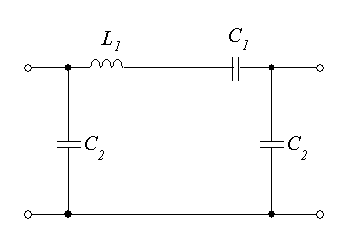
Рис 9.3

Согласно алгоритму действий получим график рис 9.4, по которому определяем, что это полосовой фильтр (см. рис. 9.1 в)

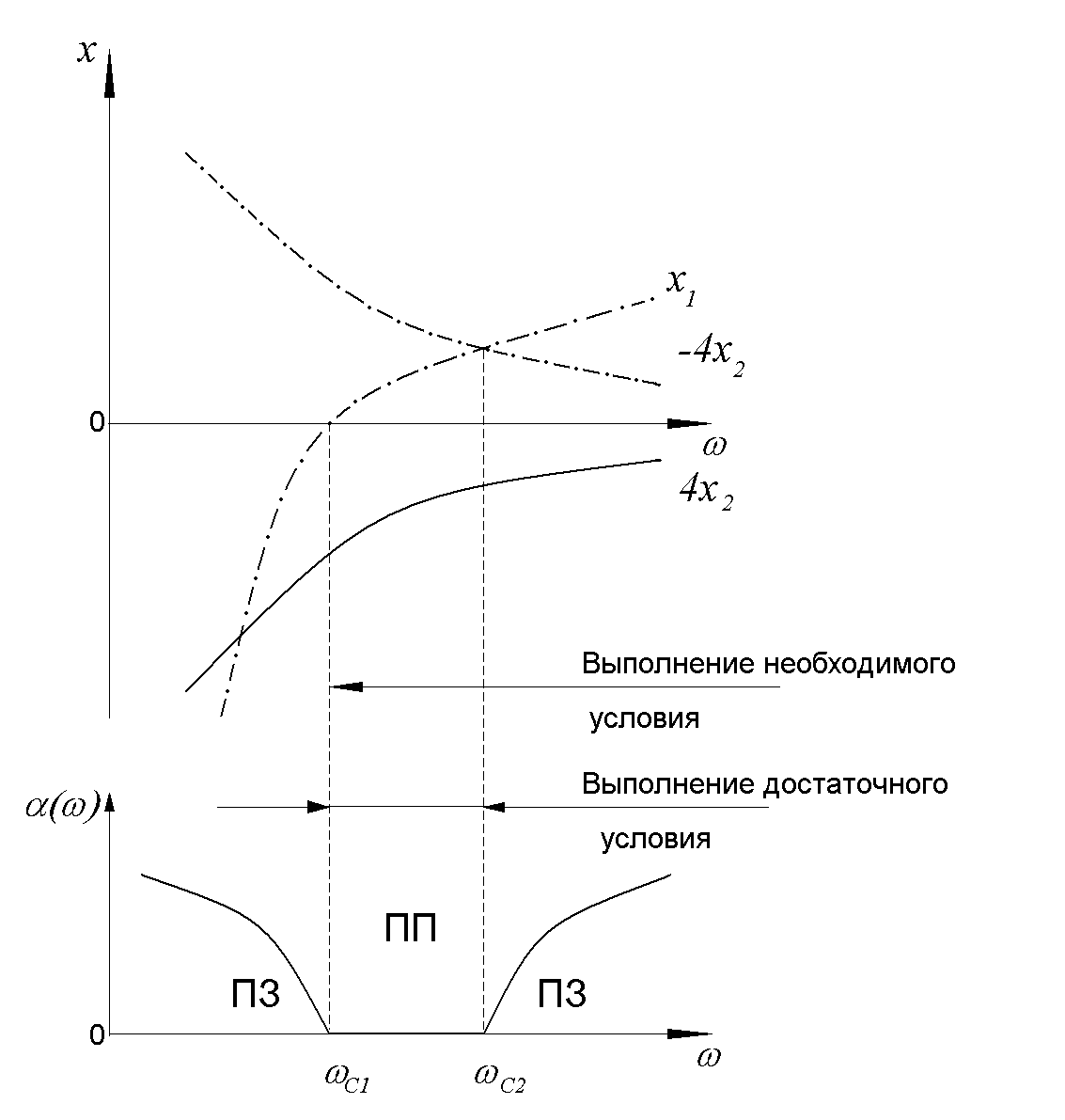
Рис 9.4