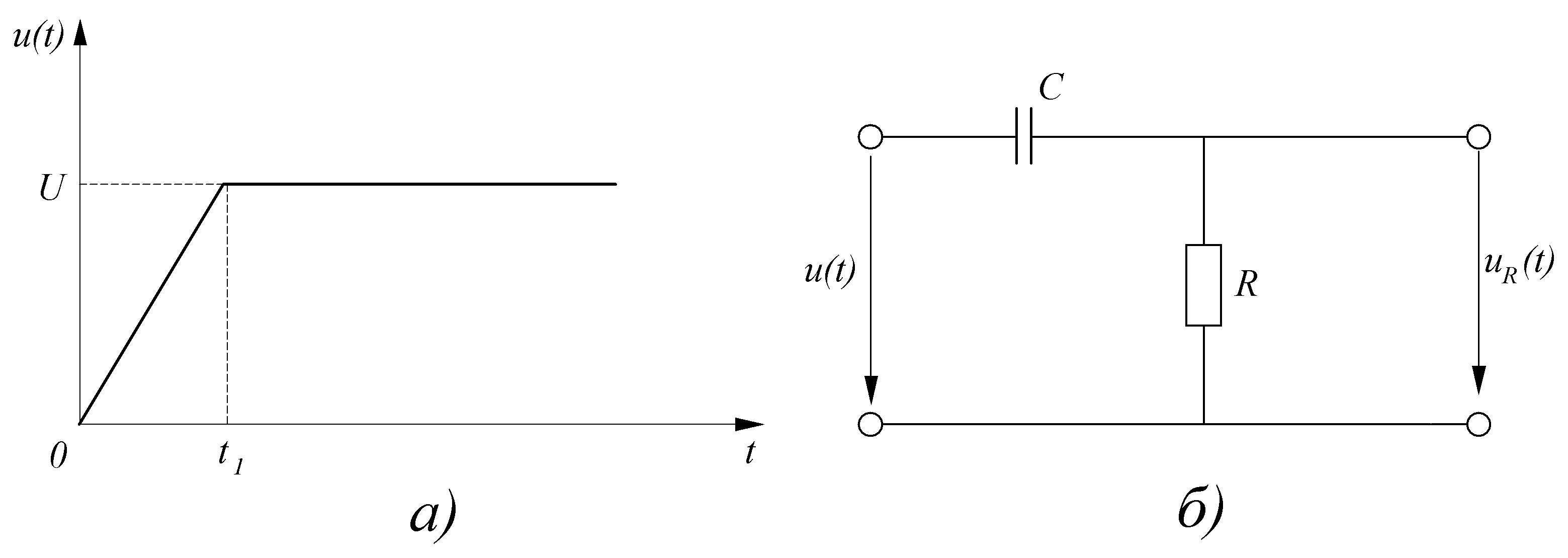5. Определение реакции цепи на произвольное внешнее воздействие

В качестве примера использования интеграла Дюамеля рассмотрим воздействие напряжения, изображенного на рис. 13.18, а, на последовательное соединение емкости и резистора(рис. 13.18,б).

Рис. 13.18

Определим напряжение на сопротивлении, для чего воспользуемся основной формой записи интеграла наложения (13.11). Для этого запишем необходимые данные:

Определим производные функции :

Переходная характеристика цепи представляет собой отклик на единичную функциюи может быть определена из рассмотрения включения постоянного напряжения в–цепь (см. п.13.2):

.

Следовательно, для ,

(13.17)

Для отклик будет определяться последствием линейно нарастающего входного напряженияи действием напряжения, т.е. для

.

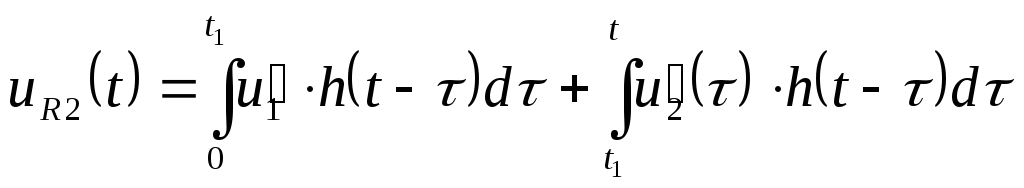Поскольку , то для,

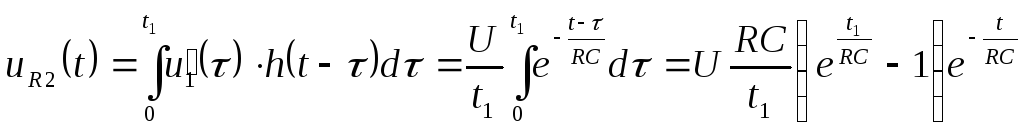. (13.18)

При формулы (13.17) и (13.18) дают одинаковые значения

.

Таким образом, функция , описывающая напряжение на сопротивлении, имеет вид:

График этой функции изображен на рис. 13.19.

Рис. 13.19.

С помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие и в том случае, когда внешнее воздействие на цепь описывается кусочно-непрерывной функцией, т.е. функцией, которая имеет конечное число конечных разрывов. В этом случае интервал интегрирования необходимо разбить на несколько промежутков в соответствии с интервалами непрерывности функции и учесть реакцию цепи на конечные скачки этой функции в точках разрыва.

Пример. Найдем реакцию цепи на внешнее воздействие, задаваемое функцией вида (рис. 13.20):

Рис. 13.20.

Решение.

Разбиваем ось времени на четыре промежутка в соответствии с интервалами непрерывной функции .

При реакция цепитождественно равна нулю (реакция цепи не может опережать по времени внешнее воздействие на цепь).

На участке , функциянепрерывна, поэтому реакция цепи определяется непосредственно с помощью выражения (13.11)

.

При интервал интегрированиясодержит одну точку разрыва функции. Разбивая интервал интегрирования на два промежуткаи учитывая реакцию цепи на воздействие скачка функциив точке, получаем

.

При интервал интегрирования содержит две точки разрыва функции.Для определения реакции цепи в этом случае необходимо разбить интервал интегрирования на три промежутка, и учесть реакцию цепи на скачки функции в точкахи. Учитывая, что при, находим:

Таким образом, алгоритм анализа переходных процессов методом наложения содержит следующие этапы.

1. В зависимости от вида входного воздействия и цепи выбирают форму записи интеграла Дюамеля.

2. Классическим или операторным методом находят переходную или импульснуюхарактеристики цепи.

3. Весь интервал интегрирования разбивают на промежутки, соответствующие интервалам непрерывности входного воздействия .

4. На каждом из этих промежутков определяют выражения функции входного воздействия и их производные.

5. Для каждого промежутка непрерывности входного воздействия записывают интеграл Дюамеля и определяют его значение. При этом учитывают реакцию цепи на конечные скачки функции в точках разрыва. Следовательно, получают переходный процесс в виде временной функции.

В заключении необходимо отметить, что метод наложения (интеграла Дюамеля) применяется при анализе воздействия на линейную цепь напряжения (тока) сложной формы при нулевых начальных условиях.

24