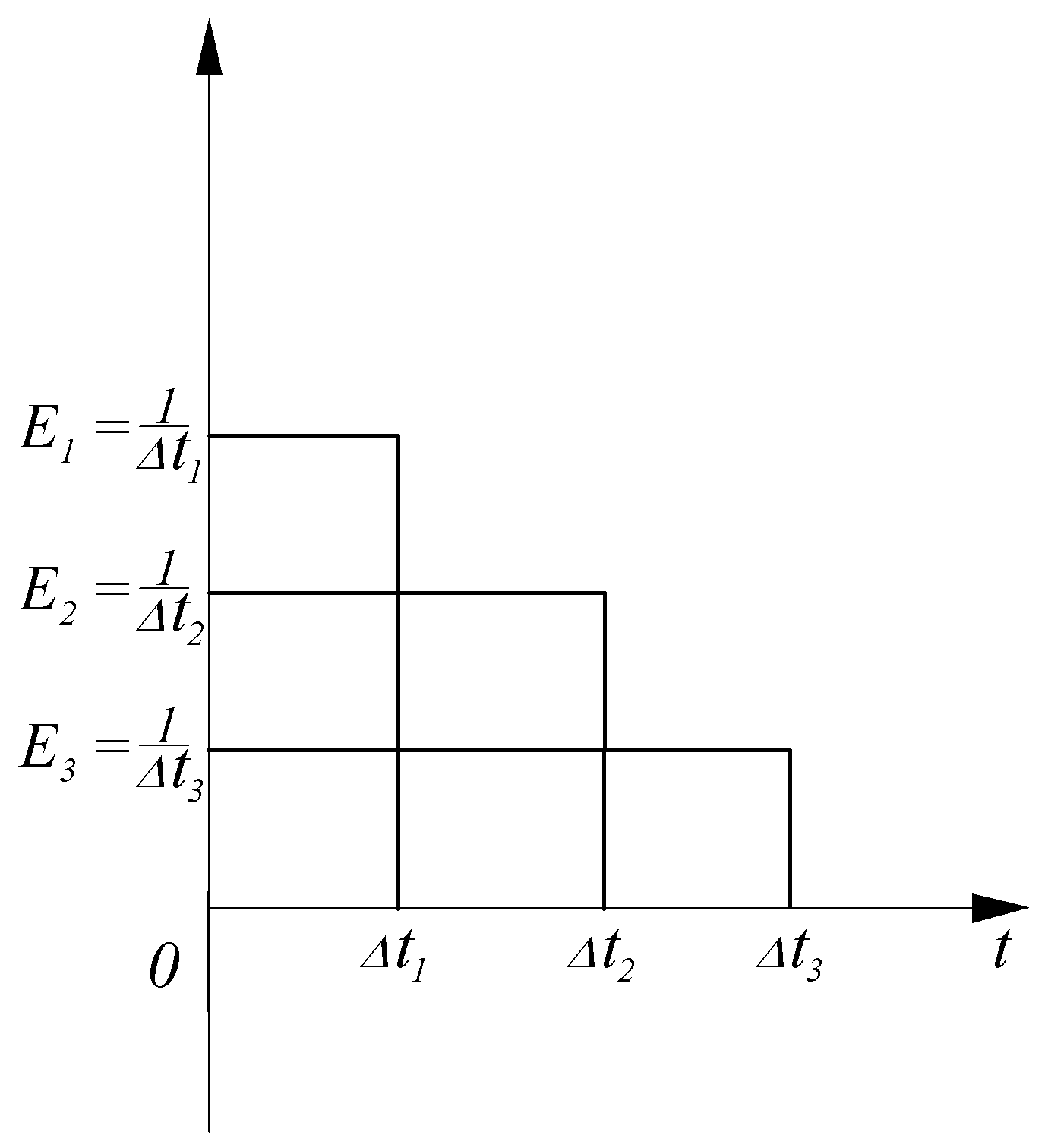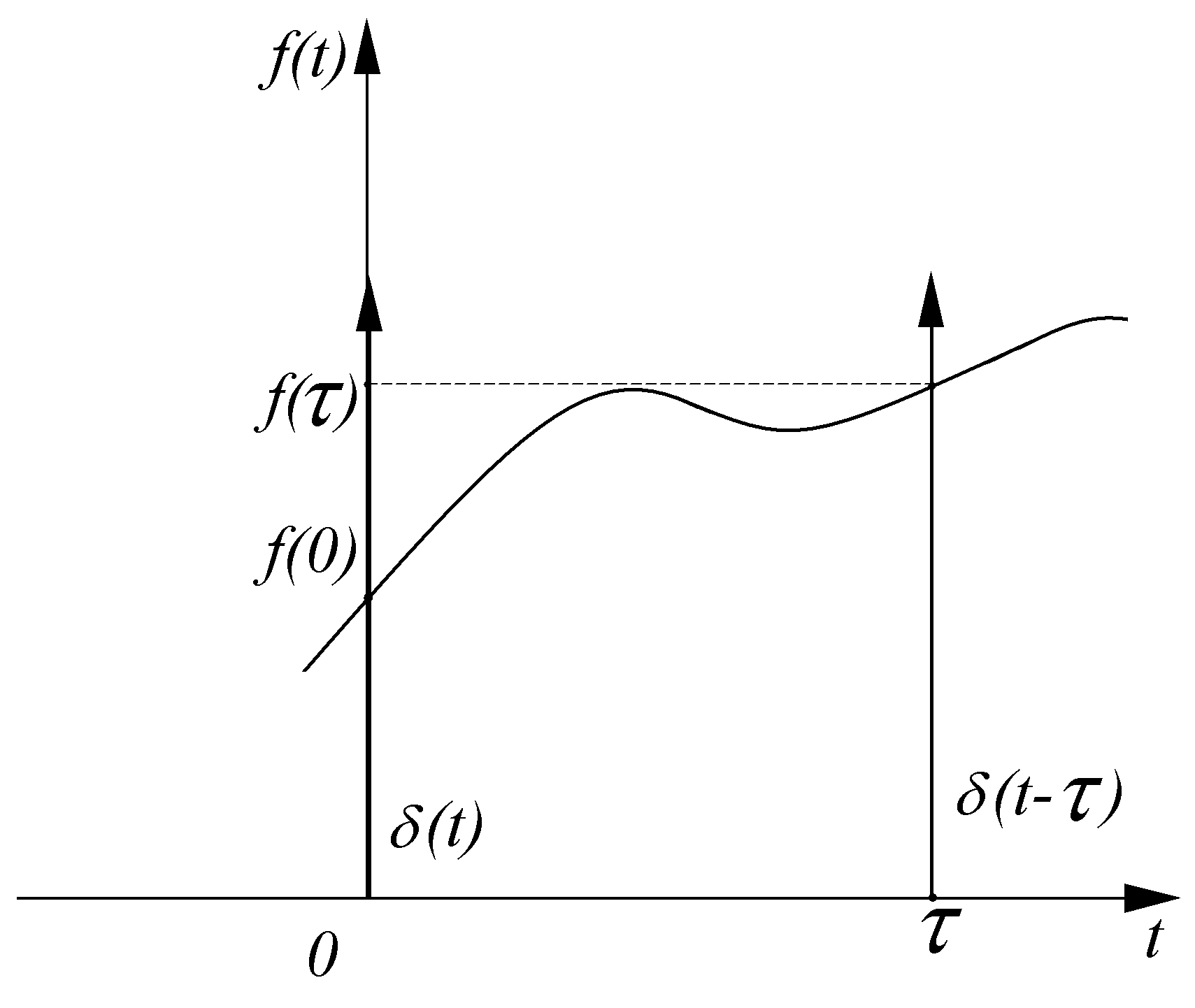- •1. Принцип суперпозиции в теории переходных процессов.
- •2. Импульсные воздействия на электрические цепи.
- •Единичная ступенчатая функция
- •Свойство функции
- •Единичная импульсная функция (функция Дирана)
- •Свойства функции
- •1. Площадь функции илиравна единице.
- •3. Переходная и импульсная характеристики электрической цепи.
- •3.1. Переходная характеристика цепи.
- •Виды переходной характеристик.
- •Решение
- •Расчет переходной характеристики операторным методом
- •3.2. Импульсная характеристика цепи
- •Решение
- •4. Интеграл наложения (дюамеля).
- •5. Определение реакции цепи на произвольное внешнее воздействие
- •Решение.
Единичная ступенчатая функция
При использовании принципа суперпозиции в качестве элементарного сигнала стандартной формы обычно используют единичный сигнал или сигнал включения (единичная ступенчатая функция, функция Хевисайда, функция включения).
Единичная
ступенчатая функция (функция Хевисайда)
называется функция
![]() ,
которая в момент времени
,
которая в момент времени![]() изменяется скачком от нулевого уровня
до значения, равного единице (рис. 13.4,а):
изменяется скачком от нулевого уровня
до значения, равного единице (рис. 13.4,а):
 (13.1)
(13.1)
Функция
![]() не имеет размерности или, как говорят,
имеет нулевую размерность. Смещенную
вправо или влево по оси времени на
отрезок
не имеет размерности или, как говорят,
имеет нулевую размерность. Смещенную
вправо или влево по оси времени на
отрезок![]() от оси ординат. Функцию Хевисайда
называют соответственнозапаздывающей
или опережающей
(рис. 13.4, б,
в)
от оси ординат. Функцию Хевисайда
называют соответственнозапаздывающей
или опережающей
(рис. 13.4, б,
в)
|
|
|
Рис. 13.4. |
и записывают в виде:
 или
или

Свойство функции
Функция
![]() обладает свойством отсечки, т.е. умножение
любой функции
обладает свойством отсечки, т.е. умножение
любой функции![]() на функцию
на функцию![]() тождественно обращает функцию
тождественно обращает функцию![]() в нуль, при
в нуль, при![]() ,
и сохраняет ее значения, при
,
и сохраняет ее значения, при![]() .
.
Свойство отсечки
единичной ступенчатой функции позволяет
математически описать во времени
звуковой сигнал, воздействия которого
на электрическую цепь начинаются в
некоторый момент времени. Например,
если при
![]() цепь подключается к источнику постоянной
ЭДС
цепь подключается к источнику постоянной
ЭДС![]() ,
то произведение
,
то произведение![]() называется ЭДС включения (рис. 13.5).
называется ЭДС включения (рис. 13.5).
|
|
|
Рис. 13.5. |

где
![]() – высота ступеньки.
– высота ступеньки.
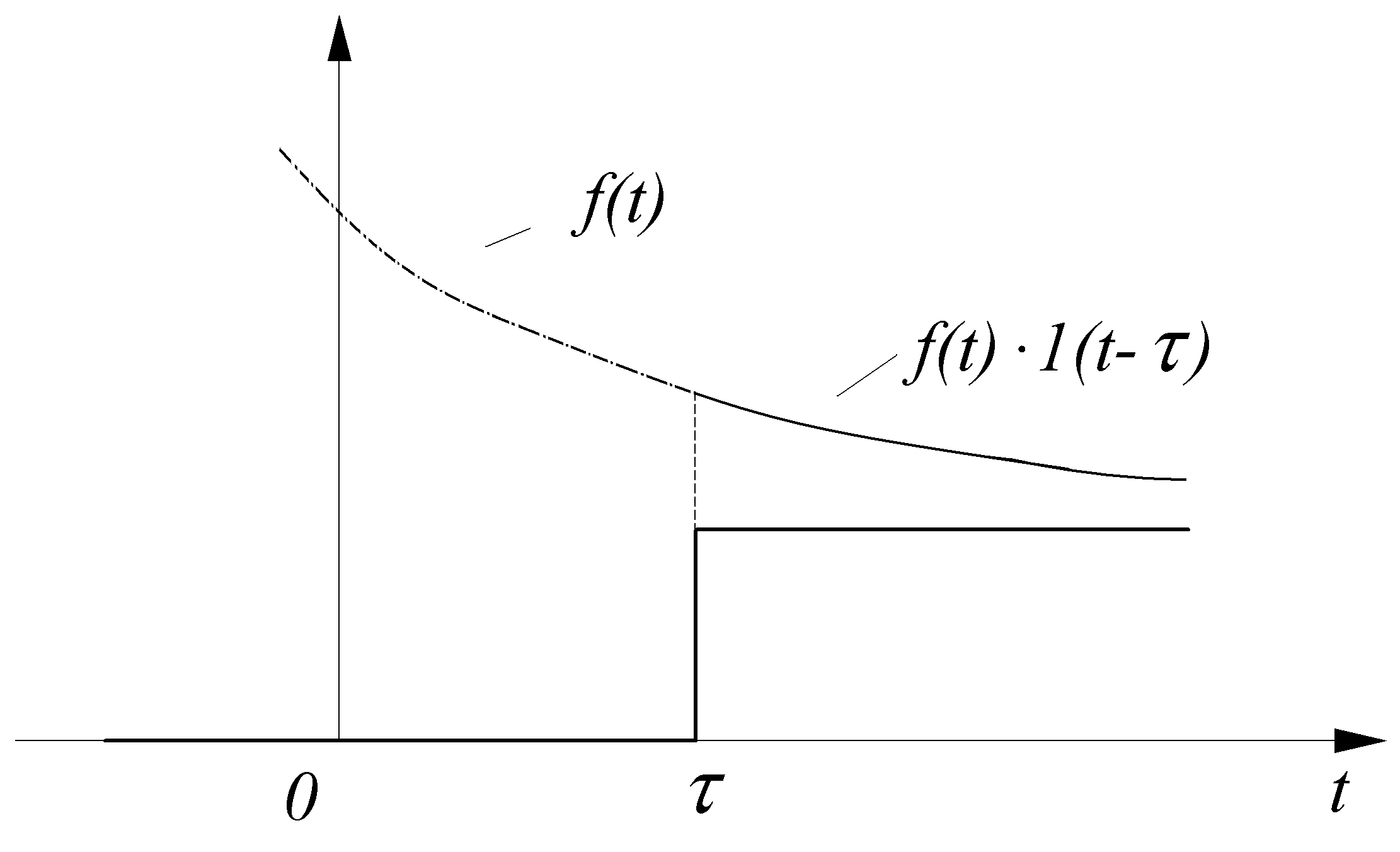
Умножение же любой
функции
![]() ,
например,
,
например,![]() ,
на запаздывающую ступенчатую функцию
,
на запаздывающую ступенчатую функцию![]() отсекает (обращает в нуль) все ее значения,
при
отсекает (обращает в нуль) все ее значения,
при![]() и сохраняет все ее значения, при
и сохраняет все ее значения, при![]() (рис. 13.6), т.е.
(рис. 13.6), т.е.

|
|
|
Рис. 13.6. |
Замечание.
Поскольку практически все сигналы,
воздействующие на электрическую цепь,
возникают в определенный момент времени,
то выражения, описывающие эти сигналы,
строго говоря, должны содержать
сомножитель
![]() .
Однако, в целях упрощения записи единичную
функцию часто опускают.
.
Однако, в целях упрощения записи единичную
функцию часто опускают.
|
|
|
Рис. 13.7. |
С помощью сложения
двух ступенчатых функций можно получить
выражение для прямоугольного импульса
длительностью
![]() (рис. 13.7)
(рис. 13.7)
![]()
Операторные
изображения функций
![]() и
и![]() по Лапласу имеют вид:
по Лапласу имеют вид:

Единичная импульсная функция (функция Дирана)
Единичное
идеализированное импульсное воздействие
произвольной формы с неограниченной
амплитудой и бесконечно малой длительностью
![]() (рис.
13.8,а)
называется дельта-функцией
(
(рис.
13.8,а)
называется дельта-функцией
(![]() )Дирана;
она задается уравнением:
)Дирана;
она задается уравнением:
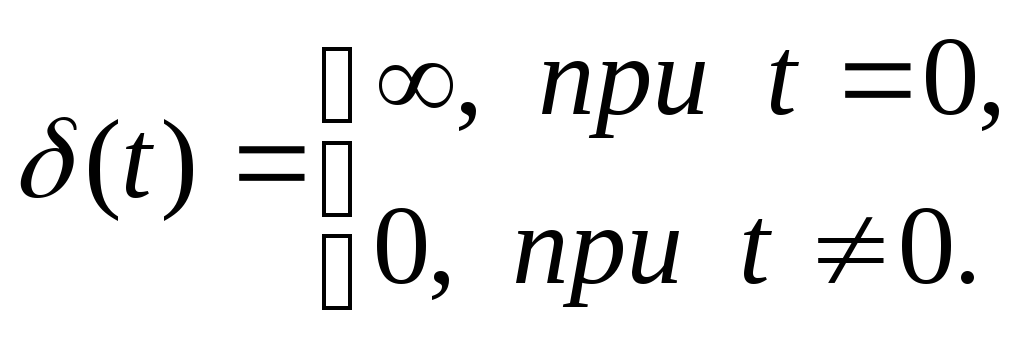 (13.2)
(13.2)
|
|
|
Рис. 13.8. |
смещенную вправо
или влево по оси времени на отрезок
![]() от оси ординат функцию Дирана называют
соответственнозапаздывающей
или
от оси ординат функцию Дирана называют
соответственнозапаздывающей
или
опережающей (рис. 13.8, б, в) и записывают в виде:
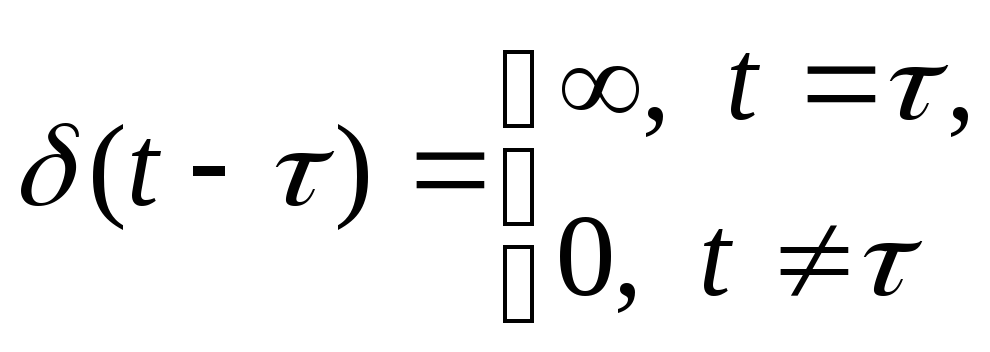 или
или

Механический аналог функции Дирана – мощный удар, мгновенный толчок. Электрический аналог – импульс с очень большой амплитудой и очень малой длительностью, которая значительно меньше наименьшей постоянной времени цепи.
Свойства функции
1. Площадь функции илиравна единице.
Действительно,
функции
![]() соответствует
импульс с амплитудой
соответствует
импульс с амплитудой
![]() и длительностью
и длительностью![]() ,
при
,
при![]() (рис. 13.9).
(рис. 13.9).
|
|
|
Рис. 13.9. |
Площадь импульсов
![]() одна и та же, и равна
одна и та же, и равна![]() .
Следовательно
.
Следовательно
![]() (13.3)
(13.3)
Аналогично
![]()
2. Из выражения (13.3) следует, что единичная импульсная функция является производной по времени единичной ступенчатой функции:
![]() (13.4)
(13.4)
3. Дельта-функция обладает фильтрующим свойством или свойством выборки.
Пусть имеем функцию
![]() (рис. 13.10). Произведение
(рис. 13.10). Произведение![]() не равно
не равно
|
|
|
Рис. 13.10. |
нулю только при
![]() ,
т.е.:
,
т.е.:![]() ,
а интеграл
,
а интеграл
![]() .
.
Произведение
![]() (см.рис. 13.9) не равно нулю только при
(см.рис. 13.9) не равно нулю только при![]() ,
а интеграл:
,
а интеграл:
![]()
Следовательно,
умножая функцию
![]() на
на![]() ,
мы как бы выбираем из множества значений
функции
,
мы как бы выбираем из множества значений
функции![]() только одно ее значение
только одно ее значение![]() ,
соответствующее времени
,
соответствующее времени![]() .
.
Заметим,
что
![]() имеет размерность, обратную времени
имеет размерность, обратную времени![]() .
.
4. Операторное
изображение
![]() по Лапласу:
по Лапласу:
![]() .
.