Дивергенция и ротор.

Дивергенцией (расходимостью) векторного поля V называется его скалярная характеристика div V, :

.

По-другому, 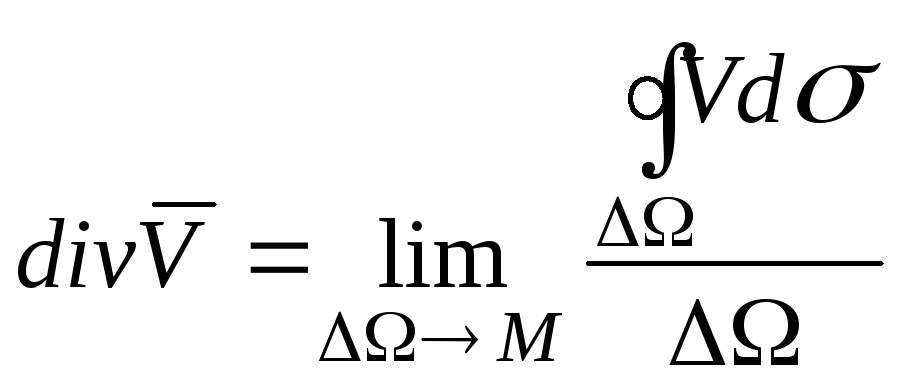, где V – векторное поле, содержащее точку М,  - объем, ограниченный поверхностью . Интеграл можно рассматривать как количество векторных линий, начинающихся внутри объема . При этом, если , то в  имеется источник векторных линий, если , то в  имеется сток векторных линий, а если , то в  источников и стоков нет либо они компенсируются.

Таким образом, div V – это плотность источника в точке М, вычисленная в малом объеме , содержащем точку  и ограниченном малой поверхностью .

Точки, в которых div V  0, называются источниками векторного поля V.

Ротор (вихрь) – это вектор, характеризующий локальное вращательное движение в данной точке векторного поля :

.

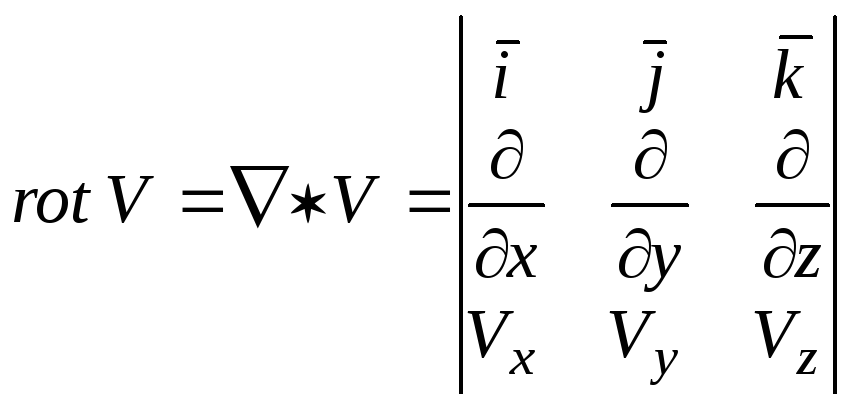Потенциальное и соленоидальное поля.

Рассмотрим физическое тело и в каждой его точке М определим скалярную функцию U(M). Тогда множество значений этой функции образует скалярное поле. Для задания такого поля достаточно определить функцию точки U(M) = U(x,y,z). Тогда можем получить векторное поле grad U(M), являющееся градиентом функции U(M). Такое векторное поле называется потенциальным.

Не всякое векторное поле является потенциальным.

- полный потенциал 

 ,

Т.е. для того, чтобы векторное поле было потенциальным, необходимо и достаточно, чтобы вихрь этого поля равнялся нулю.

При этом (векторным) потенциалом называют такое векторное поле А(M), что для любой точки М справедливо равенство V(M) = rot A(М), где V(M) – данное векторное поле.

Векторное поле V, у которого дивергенция равна нулю, т.е. выполнено тождественное условие , называется соленоидальным.