Некоторые примеры

ПРИМЕР 1. Исследовать на сходимость ряд

.

Решение. Сравним данный ряд с рядом этот ряд сходится, так как является обобщенным гармоническим, .

Используем предельный признак сравнения.

.

Так как предел конечен и не равен 0, а ряд сходится, то сходится и ряд .

ПРИМЕР 2. Исследовать на сходимость ряд

.

Решение. Имеем

,

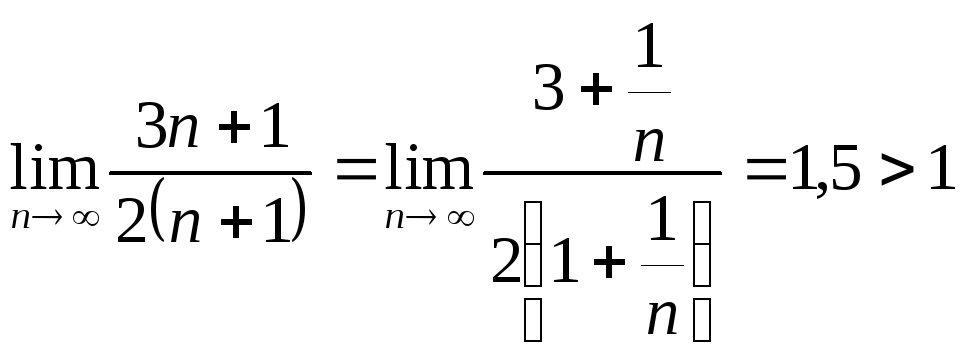следовательно, по признаку Даламбера исходный ряд расходится.

ПРИМЕР 3. Найти область сходимости функционального ряда

.

Решение. По признаку Коши (радикальному) имеем

.

При вычислении предела использован известный предел .

Итак, R=1, следовательно, данный ряд сходится, если .

Исследуем поведение ряда на концах интервала. Пусть тогда имеем числовой ряд. Этот ряд расходится, так как , т.е. не выполняется необходимое условие сходимости ряда. Итак, область сходимости ряда.

ПРИМЕР 4. Найти область сходимости степенного ряда

.

Решение. Найдем область сходимости ряда, используя признак Даламбера.

.

Таким образом, ряд сходится при . Исследуем сходимость ряда на границах. При имеем числовой ряд , который расходится по необходимому признаку. При получим знакочередующийся числовой ряд , который также расходится по необходимому признаку. Итак, область сходимости ряда.

ПРИМЕР 5. Разложить функцию f(x)=x² в ряд Фурье на интервале [-,].

Решение. , следовательно, функция f(x) – четная. Значит, . Кроме того, Т=. Тогда по формуле, .

Тогда , или .

Окончательно получим

ПРИМЕР 6. В ящике 13 деталей, из них 10 – бракованных. Наугад берут 5 деталей. Какова вероятность, того, что среди взятых деталей 3 бракованных?

Решение. Событие А состоит в том, среди взятых деталей окажется 3 бракованных. P(A)=m/n. Сначала найдем количество всевозможных исходов n. Так как берем наугад 5 деталей из 13, без учета порядка, то . Теперь найдем число благоприятных исходов m. Так как три детали должны оказаться бракованными, то оставшиеся две детали должны быть качественными (т.е. взятыми из трех годных деталей, находящихся в ящике). Таким образом, 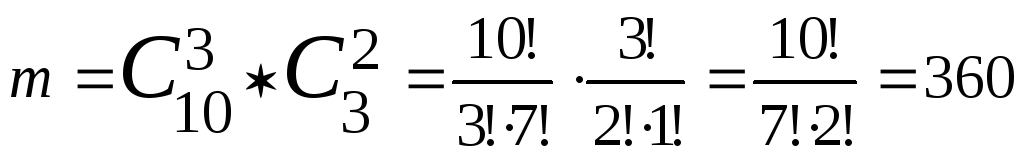. P(A)=360/1287=0,28.

ПРИМЕР 7. Всхожесть семян равна 70%. Какова вероятность того, что из 10 семян взойдут а) 8; b) по крайней мере 8?

Решение. Событие А состоит в том, что семечко взойдет. По условию задачи, n=10, p=70%=0.7, q=1-p=0.3.

а). По формуле Бернулли Р₁₀(8) = С⁸₁₀*p⁸*q^10-8 = = 45*(0.7)⁸*(0.3)² = 0.2335.

b) Р = Р₁₀(8) + Р₁₀(9) + Р₁₀(10) = 45*(0.7)⁸*(0.3)² +10*(0.7)⁹*(0.3)¹ +(0.7)¹⁰=0.38.

ПРИМЕР 8. Построить график функции распределения д.с.в., заданной законом распределения:

Х	2	4	6
Р	0.1	0.3	0.6

Решение.

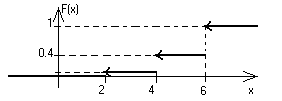
Если х £ 2, то F(x)=P(X<x)=0, т.к. нет значений с.в. Х, меньших 2.

Если 2 < х £ 4, то F(x)=P(X<x)=P(x=2)=0.1.

Если 4 < х £ 6, то F(x)=P(X<x)=P[(x=2)+(x=4)]=0.1+0.3=0.4.

Если х > 6, то F(x)=P(X<x)=P[(x=2)+(x=4)+(x=6)]=1.

График функции распределения будет выглядеть следующим образом:

ПРИМЕР 9. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины, заданной законом распределения:

Х	0	1	2
Р	0.72	0.26	0.02

Решение. Математическое ожидание М(Х)=0*0.72+1*0.26+2*0.02 = 0.3.

Дисперсия D(X)=(0-0.3)²*0.72+(1-0.3)²*0.26+(2-0.3)²*0.02 = 0.25.

Среднее квадратическое отклонение s (Х)=0.5.

ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА.

Градиент и производная по направлению.

Рассмотрим функцию двух переменных z = f(x,y). Градиентом функции z=f(x,y) в точке М₀ (х₀, у₀) называется ВЕКТОР, координатами которого являются частные производные этой функции, вычисленные в точке М₀:

, .

Градиент показывает направление, в котором скорость изменения функции максимальна, причем норма (длина) градиента равна величине этой максимальной скорости.

На плоскости ХОY выберем фиксированное направление, задаваемое вектором .

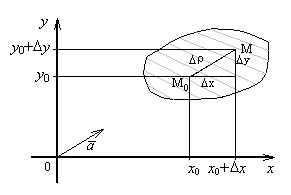
Переместим точку М₀ в области в положение М(х₀+х, у₀+у). Величины х и у называются приращение аргументов, а z = f (x₀+x, y₀+y)- f(x₀, y₀) – полным приращением функции z при переходе от точки М₀ к точке М. Тогда производной функции z=f(x, y) по направлению вектора называется предел

Производная по направлению выражает скорость изменения функции в этом направлении.

Производная по направлению есть скалярное произведение градиента на единичный вектор заданного направления, т.е.

Таким образом, для нахождения градиента функции достаточно найти ее первые частные производные и вычислить из в заданной точке А. Для поиска производной по направлению надо предварительно найти длину (норму) заданного вектора как квадратный корень из суммы квадратов координат, затем найти координаты вектора , поделив координаты исходного вектора на найденное число. После этого перемножить скалярно найденный ранее вектор градиент и полученный вектор.