
Моделювання систем модуль 1, перший рівень складності
-
*) Створення імітаційної моделі передбачає :1. Формулювання проблеми та постановка завдання.
2. Розробка концептуальної моделі.
3. Розробка та програмна реалізація імітаційної моделі, що вимагає:
* - вибір мови програмування;
* - розробка структурної схеми імітаційної моделі та опис її функціонування;
- програмна реалізація імітаційної моделі.
4. Перевірка адекватності імітаційної моделі.
5. Планування експериментів на моделі.
6. Оцінка точності результатів моделювання.
7. Інтерпретація результатів моделювання та прийняття рішень.
-
*) Лінійна математична модель передбачає :
-
*) Динамічна модель передбачає :
-
*) Статистична модель передбачає :
-
*) Математична модель: рівняння лінійної регресії має вигляд:
-
*) Метод найменших квадратів, рівняння регресії проводиться оптимально щодо: у встановленні числових значень коефіцієнтів для вибраної математичної залежності рівняння регресії.
-
*) Метод регресивного аналізу для масиву випадкових чисел передбачає:
-
*) Моніторинг за допомогою моделі полягає у: вивченні режимів штатного функціонування систем при довільній зміні їх робочих параметрів.
-
*) Про точність моделі судять по : ступені близькості її вихідних параметрів та параметрів системи.
-
*) Для побудови моделі типу „чорного ящика” слід: доступні лише вхідні та вихідні параметри системи, може бути встановленим характер зв’язку між ними. Виявляється, що для достатньо великого об’єму таких даних можна відтворити внутрішню структуру системи для побудови моделі.
-
*) Визначення: «модель, - це…
) природна (матеріальна) копія системи, що відображає основні закономірності фунціонування систем
) штучна (не матеріальна) копія системи, що відображає основні закономірності фунціонування систем
@)вірні всі відповіді
) комп’ютерна копія
-
*) Моделювання систем передбачає використання:
)структурування, виділення структурних елементів (об’єктів)
)встановлення важливості (атрибутів) структурних елементів
)встановленні підпорядкування (ієрархії) об’єктів
@)всіх дій, описаних вище
-
*) Фізична модель полягає у …
використанні матеріальних об’єктів, часового масштабування для відображення основних закономірностей роботи систем
-
*)Призначення моделювання полягає у ...
) відтворенні всіх характеристик та закономірностей функціонування систем
) проведенні розрахунків режимів функціонування систем
@ створення копії системи, що відображає її важливі характеристики
) дослідженні спостережуваних параметрів систем
-
*)Математична модель полягає у ...
) дослідженні систем з використанням метода Монте-Карло
@ відображення основних закономірностей роботи систем математичними рівняннями та символами
) використанні програмних методів та ЕОМ для дослідження систем
) описанні функціонування систем за допомогою диференційних рівнянь
-
*)Аналогова модель полягає у ...
-
*)Основні завдання теорії моделювання систем полягають у ...
) керуванні режимами роботи систем
) фіксації всіх особливостей роботи систем
@ оптимізації та моніторингу режимів роботи систем
-
*) Внутрішні параметри моделювання систем - ...
) характеризують реакцію системи на зовнішні фактори
) відтворюють детерміновані закономірності її фукціонування
@ відносно незалежні від впливу зовнішніх факторів і визначають структуру і організацію системи
) відтворюють випадкові закономірності її фукціонування
-
*) Спостережувані параметри моделювання систем - …
що визначають (формують)її вихідну функцію
-
*) Керовані параметри моделювання систем - …
характеризують вплив зовнішніх (вхідних) факторів на поведінку системи
-
*) Говорять про модель системи як „білий ящик” у випадку...
відомої структури та характеру взаємодії елементів системи
-
*) Говорять про модель системи як „сірий ящик” у випадку...
коли доступ обмежений
-
*) Точність та адекватність моделі це-...
) ідентичні поняття
@)відповідно, кількісна та якісна міра відтворення характеристик реальної системи
)точність- відображає стохастичний характер моделювання, адекватність- співпадання результатів моделювання
)вірні всі перераховані відповіді
-
*) Статистична (ймовірнісна) модель будується у випадку:
) нормального закону розподілу випадкових параметрів системи
) детермінованими процесами
@) наявності випадкових факторів при функціонуванні систем
) пуасонівських потоків випадкових подій
-
*) Регулярний потік подій:
послідовність однотипних подій, що реалізуються через однакові проміжки часу
-
*) Визначення: «Подія, це …»
це обмежене в часі явище, що настає в момент, коли приймається рішення про початок або закінчення дії
-
*) Визначення: «Процеси, це …»
це орієнтована в часі послідовність подій
-
*) Розподіл Гауса є:
розподіл
ймовірностей
випадкової
величини,
що характеризується густиною
ймовірності
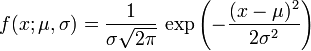
опуклою кривою?
-
*) Розподіл Пуасона є:
опуклою кривою?
-
*) Рівномірний (RNP) розподіл на інтервалі [a,b] є:
прямою?
-
*) Розподіл Гауса застосовується щодо:
-
*) Розподіл Пуасона застосовується щодо:
-
*) Рівномірний (RNP) розподіл на інтервалі [a,b] застосовується щодо:
-
*) Визначення: «Потік подій, це …»
послідовність однотипних об’єктів (подій), упорядкована в часі
-
*) Інтенсивність потоку подій дорівнює:
) числу подій за час спостереження
) послідовністі однотипних подій, що мають статичні параметри
@) число подій за одиницю часу
) послідовності однотипних подій, що реалізуються через певні проміжки часу
-
*) Функція розподілу імовірності випадкової величини P(x< а)=F(x) має зміст:
) ймовірності того, що випадкова величина x приймає значення більше числа а
) ймовірності того, що випадкова величина x приймає значення рівним числу а
) вірні всі відповіді
@) ймовірності того, що випадкова величина x приймає значення менше числа а
-
*) Розподіл Гауса, f(x)- щільність ймовірності, а – математичне сподівання, . s - середньоквадратичне відхилення випадкової величини. Зміна s приводить до…
зміни “опуклості” лінії на графіку
-
*) Розподіл Пуасона для потоку поді: t -час спостереження, і- інтенсивність потоку, к- число подій за час спостереження. Середньоквадратичне відхилення випадкових чисел дорівнює:
) і
) 1/(t*і)
@) t*і
) t
-
*) Розподіл Пуасона для потоку поді: t -час спостереження, і- інтенсивність потоку, к- число подій за час спостереження. Симетризація розподілу відбувається при:
) зменшенні величини t*і
) при добутку t*і
@) збільшенні величини t*і
) t прямує до нуля
-
*) Графік щільності розподілу Пуасона для потоку поді є :
опуклою кривою?
-
*) Графік щільності розподілу Гауса є :
опуклою кривою?
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [2, 8] здійснюється співвідношенням:
y=2+6x
-
*)Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [0, 12] здійснюється співвідношенням:
y=12x
-
*)Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [2, 20] здійснюється співвідношенням:
y=2+18x
-
*)Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [6, 9] здійснюється співвідношенням:
y=6+3x
-
*)Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [3, 9] здійснюється співвідношенням:
y=3+6x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [5, 7] здійснюється співвідношенням:
y=5+2x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [4, 10] здійснюється співвідношенням:
y=4+6x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [2, 20] здійснюється співвідношенням:
y=2+18x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 10]. Перехід до таких значень y інтервалу [2, 4] здійснюється співвідношенням:
y=2+x/5
y=2+0.2x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 6]. Перехід до таких значень y інтервалу [1, 10] здійснюється співвідношенням:
y=1+3x/2
y=1+1.5x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [3, 7] здійснюється співвідношенням:
y=3+4x
-
*) Задана рівноімовірна послідовність випадкових чисел x в інтервалі [0, 1]. Перехід до таких значень y інтервалу [5, 17] здійснюється співвідношенням:
y=5+12x
-
*) Визначення. «Система масового обслуговування, це …»
об’єкт, організація чи структура для обробки потоку однотипних заявок
-
*) Коли заявки, які обробляє система масового обслуговування можуть повертатися в неї, вона є...
замкнутою
-
*) Під дією вхідного потоку заявок СМО відбувається:
-
*) Під дією вихідного потоку заявок СМО відбувається:
-
*) Елементарна теорія функціонування СМО («народження-знищення») орієнтована на:
-
*) Хто з наведених вчених створив теорію систем масового обслуговування:
Агнер Ерланг
-
*) Елементами систем масового обслуговування є...
вхідний потік, черга, апарат обробки потоку, вихідний потік
заявки та апарати обробки потоків заявок
-
*) Параметри ефективності СМО для заявок:
) середній час обслуговування заявок
) пропускна здатність
) середній час перебування заявки в черзі
@ вірні всі перераховані відповіді
-
*)Показники ефективності використання СМО
вірні всі відповіді
-
*)Показники якості обслуговування заявок СМО
вірні всі відповіді
-
*)Відносна пропускна здатність СМО
умова обслуговування
P(0)
= ймовірності що система буде незайнята або в системі присутній хоч один незайнятий пристрій
-
*) Коефіцієнт використання СМО визначаються, як середня кількість вимог, що обслуговуються (черга СМО при цьому не розглядається), і дорівнює сумі добутків ймовірностей станів Pi на відповідну кількість зайнятих каналів i
-
*) Аналогом пристроїв СМО у інформаційних мережах є …
комп’ютер
-
*) Аналогом заявок СМО у інформаційних мережах є …
кадри / фрейми
-
*) Для інформаційних мереж завадозахищеність найкраща для …
екранованих витих пар?
-
*) Задача на умову оптимізації математичної моделі y(x)= x sin(x): Знайти y(x)' =0?
tg(x)=-x
-
*) Задача на умову оптимізації математичної моделі y(x)= x cos(x): Знайти y(x)' =0?
ctg(x)=x
-
*) Задача на умову оптимізації математичної моделі y(x)= x cos(x): Знайти y(x)' =0?
ctg(x)=x
-
*) Задача на умову оптимізації математичної моделі y(x)= x sin(x^2): Знайти y(x)' =0?
tg(x^2)=2x^2
-
*) Задача на умову оптимізації математичної моделі y(x)= x^2 sin(x): Знайти y(x)' =0?
) tg(x)=2x
) tg(x)=x
@) tg(x)=x/2
) ctg(x)=x^2
-
*) Задача на умову оптимізації математичної моделі y(x)= x cos(x^2): Знайти y(x)' =0?
) ctg(x^2)= 1/(2x^2)
) tg(x^2)=-1/(1+x^2)
@) tg(x^2)= 1/(2x^2)
) tg(x^2)= -1/(2x^2)
-
*) Задача на умову оптимізації математичної моделі y(x)= x/sin(x): Знайти y(x)' =0?
) tg(x)=2x
) tg(x)=x/2
@) tg(x)=x
) ctg(x)=x
-
*) Задача на умову оптимізації математичної моделі y(x)= x^2/sin(x): Знайти y(x)' =0?
) tg(x)=2x
) tg(x)=x
@) tg(x)=x/2
) ctg(x)=x^2
-
*) Задача на умову оптимізації математичної моделі y(x)=x^2 sin(x^2) : Знайти y(x)' =0?
tg(x)=-x^2
-
*) Задача на умову оптимізації математичної моделі y(x)=x^2+1/x^2: Знайти y(x)' =0?
) x^3=1
@) x^4=1
) x^2=1
) x^4=3
-
*) Задача на умову оптимізації математичної моделі y(x)= 3x+1/x^2: Знайти y(x)' =0?
1.5x^3 = 1
x^3=2/3
-
*) Задача на умову оптимізації математичної моделі y(x)= x^3*ехр(-х): Знайти y(x)' =0?
3/x = 1 --- ???
x^2=3
