Основні теоретичні факти.

Розглянемо на площині довільний промінь з початком у точці та відкладемо на ньому одиничний відрізок. Даний промінь із вибраною на ньому одиницею вимірювання називаютьполярною системою координат. При цьому точку називаютьполюсом, а промінь – полярною віссю системи координат.

Н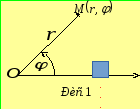ехай- довільна точка площини. Позначимо черезвідстань від неї до точки, а орієнтований кут між вибраним променем та променем- через. Очевидно, що положення точкина площині однозначно визначається числамита. Їх називаютьполярними координатами точки та записують у виді. Числоназиваютьполярним радіусом, а число -полярним кутом точки (рис. 1). Очевидно, що за змістом введених означень. Полярний кут в основному вибирають із одного з проміжківабо. В окремих випадках на кутобмежень не накладають і він може змінюватися віддо. Якщоі, де,, то точки з координатамитаспівпадають.

В окремих випадках використовують узагальнені полярні координати, коли на полярний радіус обмежень не накладають і вважають, що . При цьому привони співпадають із полярними координатами, а приприймають, що точкаспівпадає з точкою.

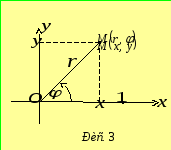
При фіксованому полярному куті та зміні полярного радіуса віддоточкапробігає всю пряму, яка проходить через полюс та утворює кутз полярною віссю. На рисунку 2 у полярній системі координат зображені точки,,,.

Накладемо на полярну систему координат прямокутну декартову так, щоб вісь містила полярну вісь, а початок координат співпадав з полюсом (рис. 3). Нехай- полярні, а- прямокутні декартові координати деякої точки. Очевидно, що виконуються співвідношення

, (1)

які виражають прямокутні декартові координати через полярні. Рівності

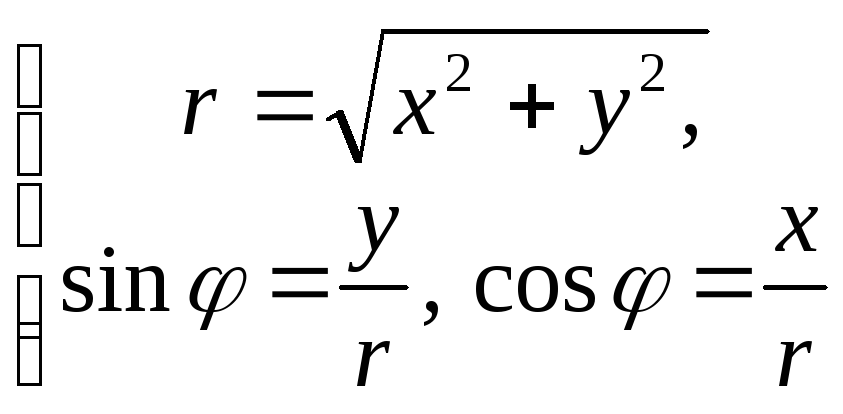(2)

д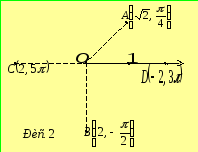озволяють виразити полярні координати точки через її декартові координати. Формули (1), (2) встановлюють зв'язок між полярними та прямокутними декартовими координатами однієї і тієї ж точки.

В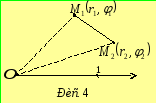окремих випадках перехід від однієї системи координат до іншої дозволяє суттєво спростити рівняння деяких ліній, що створює переваги при побудові цих ліній, а також при певних обчисленнях, зв’язаних із визначенням певних кількісних характеристик ліній.

Нехай у полярній системі координат задані дві точки та(рис. 4). Довжину відрізкаможна обчислити, застосувавши до трикутникатеорему косинусів:

. (3)

Якщо точки талежать на одній прямій і не утворюють трикутник, то у випадку, коли точкалежить поза відрізкоммаємо. Якщо ж точканалежить відрізку, то. Обидва одержані співвідношення є частинними випадками формули (3), оскільки у першому випадку, а у другому.

Нехай трикутник заданий координатами своїх вершин:,, причому(подвійна рівність не допускається, оскільки у цьому випадку точки не будуть утворювати трикутник). Обчислимо його площу.

При розташуванні вершин трикутника так, як зображено на рис. 5_а, дістаємо

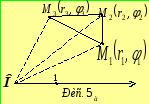
. (4)

У випадку, зображеному на рис. 5_б, маємо , що відповідає попередньому співвідношенню.

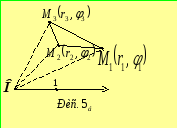
Я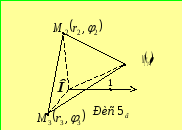кщо ж задані точки розташовані так, як зображено на рис.5_в, то .Але, оскільки тут кут між сторонамитадорівнює, а його синус дорівнює, то і у цьому випадку має місце отримана вище рівність. Таким чином, в усіх розглянутих випадках площу трикутника можна знаходити, як модуль правої частини рівності (4).

Розглянемо приклади деяких ліній, заданих своїми рівняннями в полярній системі координат. При цьому рівняння називатимемо рівнянням лінії, якщо його задовольняють ті і тільки ті пари чисел, які визначають точки на лінії.

Приклад 1. - рівняння кола з центром у полюсі, радіус якого(рис. 6).

Приклад 2. - промінь із початком у полюсі , який утворює з полярною віссю кут - у звичайній полярній системі координат, або пряма, яка містить даний промінь - в узагальненій полярній системі координат.

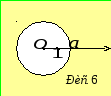
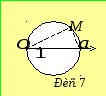
Приклад 3. - коло з центром на полярній осі, яке проходить через полюс і має діаметр(рис. 7). Для доведення даного твердження достатньо перейти до прямокутних декартових координат або використати рисунок 6, з якого видно, що точканалежить колу тоді і тільки тоді, коли виконується рівність.

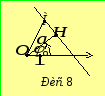
П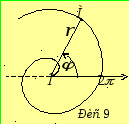риклад 4. - пряма, яка проходить на відстанівід полюса (рис. 8). Тут- полярний кут точки. Доведення даного факту випливає з того, що для довільної точкипрямої виконується рівність.

Приклад 5. - так звана спіраль Архімеда (рис. 9). Її описує точка, яка, знаходячись на промені, рівномірно віддаляється від точкипри рівномірному обертанні променя. Ця властивість використовується в техніці при створенні механізмів, які перетворюють рівномірний обертальний рух у рівномірно поступальний. Кожний наступний виток спіралі віддалений від полюса надальше, ніж попередній.

Рекомендуємо самостійно дослідити питання, як проходить спіраль Архімеда ще у трьох випадках, коли ;та, використовуючи узагальнені полярні координати.

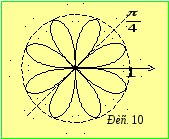
Приклад 6. Побудуємо лінію, яка у прямокутній декартовій системі координат задана рівнянням . Очевидно, що це лінія десятого порядку. Для її побудови перейдемо до полярних координат. Підставляючи у задану рівність співвідношення, після очевидних перетворень дістаємо.

Використавши двічі тотожність , отримаємо рівняння лінії в полярних координатах у виді. Для зображення лінії зауважимо, всі її точки розташовані всередині кола, радіус якого дорівнює 1, а також те, що, оскільки функціяперіодична з періодом, то її графік достатньо побудувати на проміжку, який має довжину періоду, наприклад, на проміжку, а потім періодично повторити. При зміні полярного кутавід 0 дополярний радіусзростає від 0 до 1. Якщозростає віддо, тоспадає від 1 до 0. Наведені міркування дозволяють виконати зображення лінії у вигляді восьмипелюсткової троянди (рис. 10).

Нехай точка є фокусом, а пряма- відповідною директрисою лінії другого порядку з ексцентриситетом. Побудуємо полярну систему координат, вибравши фокусполюсом та спрямувавши полярну вісь по прямій, яка перпендикулярна до директриси, але так, щоб вона не перетинала пряму(рис. 11). Будемо вважати, що відстань від точкидо прямоїрівна. Нехай- довільна точка лінії, яка є конічним перерізом (тобто еліпсом, гіперболою або параболою). Тоді рівняння лініїу вибраній системі координат запишеться у виді

.

О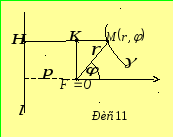держане співвідношення називаютьрівнянням конічних перерізів у полярних координатах. При рівняння задає еліпс, при- параболу, а при- гіперболу.