Приклади розв’язання задач.

Задача 1. Довести, що точка є центром ваги трикутника (точкою перетину медіан) тоді і тільки тоді, коли виконується рівність .

Доведення. Нехай точка є точкою перетину медіан та (рис. 5). Тоді , де – діагональ паралелограма . Оскільки точка – середина відрізків та , то . За відомою властивістю медіан трикутника , тому . Отже, .

Навпаки, нехай виконується рівність , тобто . Тоді , де – середина відрізка . З рівності випливає, що точки та лежать на одній прямій, а також, що – медіана трикутника. Оскільки , то точка є точкою перетину медіан.

Задача 2. У п’ятикутнику ABCDE точки K,L,M,N – середини відповідно сторін AB, BC, CD та DE, а точки R і S – середини відрізків KM та LN. Довести, що та (рис. 6).

Доведення. Введемо позначення: . Тоді

.

Знайдемо вектор .

.

Оскільки

та

,

то

.

Із одержаної векторної рівності випливає, що та .

Задача 3. В опуклому чотирикутнику точки та – відповідно середини сторін і . Довести, що якщо , то .

Доведення. Очевидно, що та . Додавши одержані рівності, дістаємо , звідки . Але за умовою . Рівність можлива тільки тоді, коли вектори та спів напрямлені, тобто, коли відрізки та паралельні. Отже, .

Задача 4. Що можна сказати про два ненульові вектори та , для яких виконується одна із рівностей: 1) , 2) , 3) ?

Розв’язання. 1). Вектори та співпадають із діагоналями паралелограма, побудованого на векторах та . Оскільки, згідно із умовою задачі, довжини цих діагоналей рівні, то паралелограм є прямокутником. Отже, вектори та перпендикулярні. 2)-3). Із нерівності трикутника випливає, що вектори та колінеарні. Рівність 2) можлива тільки у випадку, коли дані вектори співнапрямлені. Рівність 3) виконується при умові, коли вектори напрямлені протилежно, причому довжина вектора більша або дорівнює довжині вектора .

Задачі для самостійного розв’язання.

1. За заданими векторами та побудувати вектори:

1) ;

2)

3)

4)

2. Нехай - паралелограм і - точка перетину діагоналей, і - середини паралельних сторін та Побудуйте вектори:

а)

б)

в)

г)

д)

е)

3. У вектор та вектор Побудувати вектори ; ; ; .

4. Нехай - паралелепіпед, - точка перетину діагоналей, - середини відповідно сторін і За допомогою вказаних точок та точок, які є вершинами паралелепіпеда, записати вектори, рівні наступним векторам:

а)

б)

в)

г)

5. Нехай - паралелограм та - точка перетину діагоналей, і - середини паралельних сторін та Побудуйте вектори:

а)

б)

в)

г)

д)

е)

6. Як зміниться вектор, якщо його помножити на число , якщо:

1) ;

2) ;

3)

4) ?

7. Задано вектор , довжина якого 7. Знайти вектор, напрямлений протилежно до , довжина якого 5.

Дано три довільні точки . Побудувати точку таку, щоб виконувалася рівність .

8. Про вектори та відомо, що , 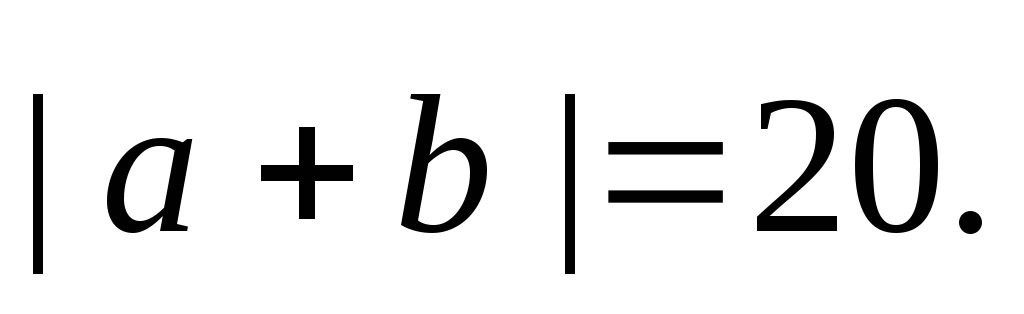Обчислити:

9. Довести, що для довільних векторів та виконуються співвідношення:

1) ;

2) .

При якій умові виконується рівність?

10. При яких умовах мають місце наступні співвідношення:

1) =

2) >

3) <

11. У кожному з випадків встановити, чи існують вектори, для яких одночасно виконуються нерівності:

а) < та <

б) > та >

12. При якій умові вектор ділить пополам кут між векторами та ?

13. При якій умові вектори та колінеарні?

14. У трикутнику вектори та напрямлені по медіанах. Знайти їхню суму.

15. Медіани трикутника перетинаються у точці Обчислити довжину вектора .

16. Обчислити довжину вектора, який є сумою всіх векторів з початком у центрі та кінцями у вершинах правильного многокутника.

17. Довести, що існує трикутник, сторони якого рівні і паралельні медіанам даного трикутника.

18. Точки - середини сторін . Довести, що , де - довільна точка простору.

19. Задано паралелограм та довільна точка простору Доведіть, що

20. Відомо, що - довільні точки простору, точка - середина відрізка і точка - середина відрізка . Довести, що .

21. Для деякого просторового чотирикутника та довільної точки простору виконується співвідношення Довести, що - паралелограм.

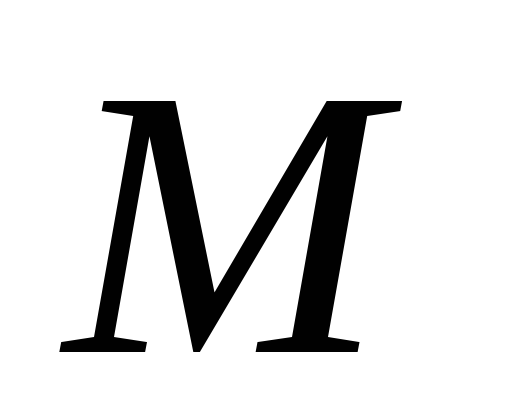22. Задано деякий чотирикутник . Точка - середина сторони 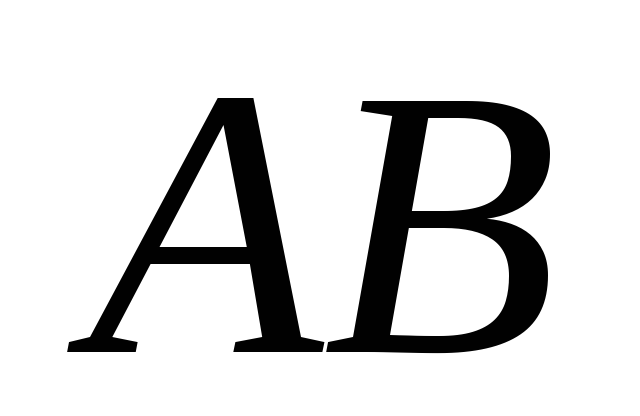і точка - середина Відомо, що має місце співвідношення Доведіть, що чотирикутник - трапеція або паралелограм.

23. Довести векторним методом теореми про середні лінії трикутника та трапеції.

24. На кожній із двох прямих вибрано по три точки та , причому виконується рівність . Довести, що середини відрізків , , лежать на одній прямій.

25. Через середину ребра та центр ваги основи піраміди проведено пряму, яка перетинає площину 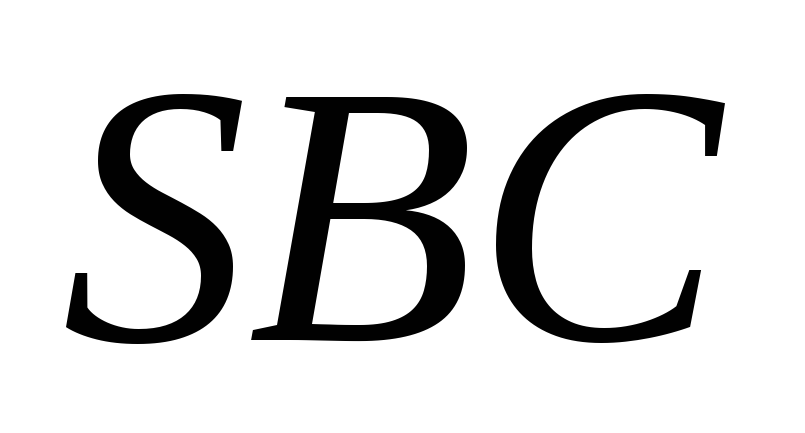у точці . Довести, що .