1.1. Доведення нерівностей за допомогою означення

За означенням вважається, що (), якщо різницяє додатним (від’ємним) числом. Тому для доведення нерівностіна заданій множині значень зміннихдостатньо розглянути різницюі показати, що вона додатна при заданих значеннях змінних. Аналогічні міркування можна застосовувати для доведення нерівностей виду.

Наведемо приклади таких доведень.

Задача 1.1.1.Довести, що для довільнихвиконується нерівність

(нерівність Коші).

Доведення.Розглянемо різницюі покажемо, що вона не може бути від’ємною. Маємо

.

Очевидно, що вираз не може бути від’ємним при довільних невід’ємних значенняхта. Тому різницяневід’ємна. Це означає, що. Відмітимо, що знак рівності можливий тоді і тільки тоді, коли.

Задача 1.1.2.Довести, що.

Доведення.Утворимо різницю

і покажемо, що вона додатна. Перегрупувавши доданки, дістаємо

.

Очевидно, що одержаний вираз додатний при довільних значеннях ,та. Нерівність доведена.

Задача 1.1.3.Довести, що якщо, то.

Доведення.Перетворимо різницюнаступним чином:

.

Оскільки за умовою , то одержаний вираз не може бути від’ємним. Це завершує доведення нерівності. Знак рівності можливий у випадках, колита.

Задача 1.1.4. Довести, що якщо, то.

Доведення.Маємо

.

Задача 1.1.5.Довести, що для довільноговиконується нерівність

.

Доведення. Маємо

.

Цим самим нерівність доведена.

Задача 1.1.6.Довести, що якщо,, то

.

Доведення. Знаходимо

.

Отже, якщо ,, то.

Задача 1.1.7.Довести нерівність(- додатні числа).

Доведення.Маємо

.

Зауважимо, що доведена нами нерівність використовується при доведенні інших нерівностей методом підсилення (див., наприклад, задачу 1.5.12).

Задача 1.1.8. Довести, що якщо, то.

Доведення. Маємо

.

Згідно з умовою задачі перший множник одержаного виразу додатний, а два інші - від’ємні, тобто весь вираз додатний.

Задача 1.1.9. Довести нерівність.

Доведення.Доведення випливає з наступних перетворень:

.

Знак рівності можливий лише у випадку, коли .

Задача 1.1.10. Довести, що якщо, то

.

Доведення.Доведення випливає із наступних співвідношень:

.

Задача 1.1.11. Довести нерівність.

Доведення. Виконаємо перетворення:

.

Оскільки , а виразприймає тільки додатні значення (дискримінант даного квадратного тричлена відносно довільної змінної від’ємний), то нерівність доведена. Знак рівності можливий тоді і тільки тоді, коли.

1.2. Синтетичний метод доведення нерівностей

Суть цього методу полягає в тому, що за допомогою певних перетворень нерівність, яку потрібно довести, виводять із деяких відомих (очевидних, або їх ще називають опорних) нерівностей. В ролі таких часто використовують нерівності:

а) , б)при, в)при,

г) при.

Логічна схема такого доведення виглядає у вигляді імплікацій

,

де - деяка початкова вірна нерівність,- отримані з неї вірні нерівності,- нерівність, яку потрібно довести. Даний метод є достатньо ефективним, проте не завжди зрозуміло, з яких очевидних нерівностей потрібно розпочинати доведення. Відповідь на це питання іноді може дати аналітичний метод, який ми розглянемо у наступному пункті.

Наведемо приклади деяких доведень, де використовується синтетичний метод.

Задача 1.2.1.Довести, що для довільних,виконується нерівність

.

Доведення.Нам відомо, що при заданих обмеженнях на змінні виконуються нерівності,. Застосувавши нерівність Коші до лівих частин записаних нерівностей та використавши записані вище співвідношення, дістаємо

,

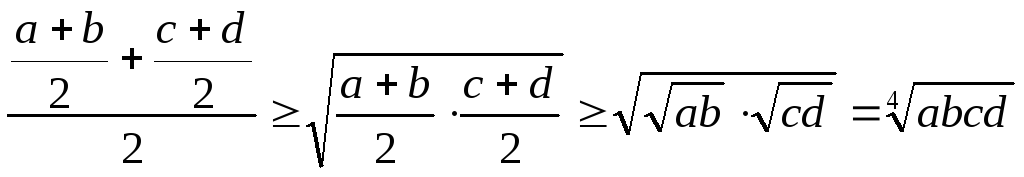або . Рівність можлива тоді і тільки тоді, коли одночасно виконуються умовита, тобто, коли.

Задача 1.2.2.Довести, щодля.

Доведення.Використаємо у ролі опорних наступні нерівності Коші:

,,,…,

,.

Перемноживши їх, дістаємо

.

Оскільки у першій опорній нерівності при рівність неможлива, то остаточно отримуємо строгу нерівність, тобто, що.

Задача 1.2.3.Довести, що при,виконується нерівність

.

Доведення.Перший спосіб. Використаємо очевидні нерівності,та. Додавши їх, дістаємо. Запишемо одержане співвідношення у виді

,

або

.

Винісши у лівій частині нерівності за дужки вираз , отримуємо нерівність, яку потрібно було довести. Знак рівності виконується при.

Другий спосіб. Використаємо розглянутий вище спосіб доведення нерівностей за допомогою означення. Для цього виконаємо наступні перетворення:

.

Отже, задана нерівність вірна.

Задача 1.2.4. Довести нерівність ( нерівність Коші – Буняковського)

.

Доведення. Розглянемо очевидні нерівності

,, ,.

Додавши їх, отримаємо нерівність , яка виконується при довільному дійсному числі. Оскільки старший коефіцієнтодержаного квадратного відноснотричлена додатний, то його дискримінант не може бути додатним. Тому

.

Звідси отримуємо потрібну нерівність.

Задача 1.2.5. Довести, що для довільних додатних чиселвиконується нерівність.

Доведення. Використаємо, як опорні, дві очевидні нерівностіта. Додаючи їх, отримуємо нерівність, яку потрібно було довести. Знак рівності виконується тільки у випадку, коли.

Задача 1.2.6. Довести, що для довільних дійсних чиселвиконується нерівність.

Доведення. Додавши очевидні нерівності, отримуємо

.

З одержаного співвідношення випливає нерівність, яку ми доводимо. Рівність виконується тільки у випадку .

Задача 1.2.7.Довести, що привиконується нерівність

.

Доведення. Розглянемо очевидні нерівності

,, ,.

Додавши їх, отримаємо нерівність

,

яка виконується при довільному дійсному числі . Тому на дискримінантодержаного відносноквадратного тричлена накладаємо умову

.

Звідси отримуємо потрібну нерівність. Дещо пізніше ми розглянемо інші способи доведення подібних нерівностей, зокрема із використанням скалярного добутку та його властивостей.

Задача 1.2.8.Довести, що для довільних додатних чиселвиконується нерівність

.

Розв’язання.Додавши три очевидні нерівності

,,,

отримуємо потрібну нерівність.