
- •Кафедра Систем управления,
- •Содержание
- •Глава 1. Автоматические системы управления ........ 7
- •1.2. Математические модели физических систем ……. 15
- •Глава 2. Цифровые системы управления .................. 47
- •Глава 1 модуля содержит описание самых распространенных автоматических систем управления – систем автоматического регулирования.
- •Глава 2 модуля содержит описание цифровых систем управления.
- •Глава 1. Автоматические системы управления
- •Синтез систем управления.
- •Обратное преобразование Лапласа имеет вид
- •Часто бывает необходимо определить установившееся, или конечное, значение y(t). Теорема о конечном значении гласит, что:
- •Где o(s) есть полином системы, учитывающий начальные условия, а
- •Глава 2. Цифровые системы управления
- •Дискретный способ вычисления временных характеристик. Если ввести аппроксимацию производной
- •Тесты по темам модуля
- •Список рекомендованной литературы
- •Словарь основных понятий и сокращений
Обратное преобразование Лапласа имеет вид
f(t)
=
![]() ,
(1.3.2)
,
(1.3.2)
где j – мнимая единица (j2 = – 1), а интегрирование в (1.3.2) проводится по бесконечно удаленному контуру комплексной плоскости для действительного значения переменной s.
Для практического применения используют таблицы преобразований Лапласа (Web-сайт MCS), полученные на основании выражений (1.3.1) и (1.3.2). Пример показан в таблице 1.3.1.
Переменную s в преобразовании Лапласа можно рассматривать как оператор дифференцирования
s
![]() .
(1.3.3)
.
(1.3.3)
Аналогично можно ввести оператор интегрирования
![]() .
(1.3.4)
.
(1.3.4)
Продемонстрируем использование преобразования Лапласа для решения дифференциальных уравнений (типа 2.1.3) с постоянными коэффициентами. Преобразование Лапласа уравнения (2.1.3) дает в соответствии с таблицей 1.3.1
B[s2Y(s)–sy(0)–dy(0)/dt]+C[sY(s)–y(0)] + DY(s) = X(s). (1.3.5)
Если x(t) = 0 (входной сигнал отсутствует), y(0) = y0 и dy(0)/dt = 0, то
Bs2Y(s) – Bs y0 + CsY(s) – Cy0 + DY(s) = 0. (1.3.6)
Таблица 1.3.1
|
f(t) |
F(s) |
|
Ступенчатая функция Хевисайда, (t) |
1/s |
|
Импульсная функция Дирака (t) |
1 |
|
tn |
n!/sn+1 |
|
sin( t) |
/(s2 + 2) |
|
cos( t) |
s /(s2 + 2) |
|
exp(-at) |
1/(s + a) |
|
f(k) (t) = dk f(t)/d tk |
skF(s)-sk-1f(0)- sk-2f’(0)-…- - sf(k-1)(0) |
|
|
F(s)/s
+ (1/s)
|
|
exp(-at) sin( t) |
/[(s2 + a2) + 2] |
|
exp(-at) cos( t) |
(s + a)/[(s2 + a2) + 2] |
Выражая отсюда Y(s), получим образ выходного сигнала
Y(s)
=
![]() .
(1.3.7)
.
(1.3.7)
Если полином q(s) = Bs2 + Cs + D, стоящий в знаменателе (1.3.7), приравнять нулю, то получим характеристическое уравнение, названное так потому, что его корни (или полюса) определяют характер движения системы. Корни полинома p(s) = (Bs + + C)y0, стоящего в числителе (1.3.7), называют нулями системы. В полюсах функция Y(s) обращается в бесконечность, а в нулях она становится равной нулю. Расположение полюсов и нулей на комплексной s-плоскости определяет характер собственного (свободного) движения системы.
Полином q(s) можно записать в виде
q(s) = (s – s1) (s – s2), (1.3.8)
где s1 и s2 – корни полинома.
Тогда
Y(s)
=
![]() .
(1.3.9)
.
(1.3.9)
Пример 1.3.1. Рассмотрим частный случай, когда D/B = 2, а С/B = 3. Тогда выражение (1.3.9) примет вид
Y(s)
=
![]() .
(1.3.10)
.
(1.3.10)
Положение полюсов и нуля этой функции на s-плоскости показано на рис. 1.3.1, где s = + j
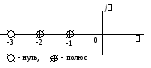
Рис. 1.3.1
В общем случае, разложив (1.3.9) на элементарные дроби, получим
Y(s)
=
![]() ,
(1.3.11)
,
(1.3.11)
где k1 и k2 – коэффициенты разложения, называемые вычетами.
Теперь применим к (1.3.11) обратное преобразование Лапласа
y(t)
= L-1{![]() }=L-1{
}=L-1{![]() }+L-1{
}+L-1{![]() }.
}.
(1.3.12)
С помощью таблицы 1.3.1 находим решение
y(t) = k1exp(s1 t) + k2 k1exp(s2 t) (1.3.13)
уравнения (2.1.3) в отсутствии входного воздействия, т.е., так называемое, свободное движение системы.
