Вправи для закріплення матерії

1. Нехай A = { 1, 2, 3, 4 }, B = { 2, 4, 6, 8 }, C = { 3, 4, 5, 6 }.

ЗнайтиAB, AC, BC, BB, (AB)C, A(BC), AB, A C,

B C, BB, (AB)C, A(BC).

2. Нехай W = { João, José, Paulo } іV = { Vera, Maria }.Знайти W × V,

V × W, V × V.

3. Припустимо, що (x + y, 1 )і( 3,x - y)рівні.Знайти x і y.

4. Припустимо, що впорядковані пари ( y - 2, 2x + 1 ) = ( x - 1, y + 2) . Знайти x і y.

5. НехайA = {a, b, c}, B = {b, c, d}, C = {a, d}.Побудувати діаграму дерево для

A × B × C.

6. НехайA = {a, b}, B = { 2, 3 }, C = { 3, 4 }.Знайти:

a) A × ( B C ) ; c) A × ( B C );

b) ( A × B ) ( A ×C ); d) ( A × B ) ( A ×C ).

7. Довести, щоA × (BC ) = (A × B)( A ×C ).

8. НехайS = { a, b }, W = { 1, 2, 3, 4, 5 }, V = { 3, 5, 7, 9 }.Знайти( S × W )( S × V ).

9. Нехай A = B  C. Довести, що:

a) A × A = (B × B) ( C × C ).

b) A × A = (B × C) ( C × B ).

10. Побудувати множини в координатній площині:

a) [1, 4] × [-2, 3]; c) [-3, 3] × [-1, 2];

b) [-2, 3] × [-3, ); d) [-3, 1] × ( - , 2].

11. Довести властивість

12. Довести, що з слідує .

13. Довести, що:

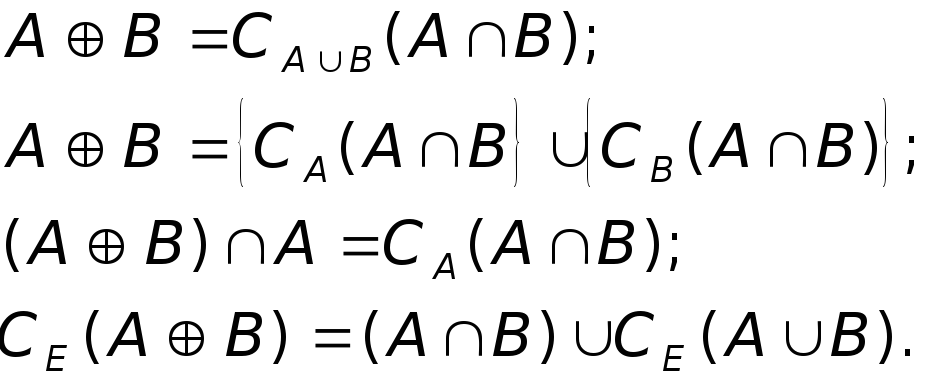
14. Нехай . Довести, що  .

15. Довести закони де Моргана

a) C ( A B) = C(A)C(B) ;

b) C( A B) = C(A)C(B) .

16. НехайU = { 1, 2, 3, 4, 5, ... ,12 }, A = { 1, 3, 5, 7, 9, 11 }, B = { 2, 3, 5, 7, 11 },

C = { 2, 3, 6, 12 } e D = { 2, 4, 8 }. Знайти множини:

a) A  B; d) A \ B;

b) A C; e) C \ D;

c) (A B)Cc; f) B D.

17. Зобразити на числовій прямій множини:

a) [ 0, 3 ] [ 2, 6 ]; d) [ 0, 3 ] [ 2, 6 ];

b) [ 0, 3 ] [ 2, 6 ]; e) [ 0, 3 ]c;

c) [ 0, 3 ] \ [ 2, 6 ]; f) [ 0, 3 ] .

18. НехайA ={ 1, 2, 3, 4, 5 }, B = { 2, 4, 6, 8, 10 }.Знайти множини:

a) A  B; c) (A B) \ (AB);

b) A B; d) (A \ B) (B \ A).

Відповіді.

1. A B = {1, 2, 3, 4, 6, 8}; AC = {1, 2, 3, 4, 5, 6}; BC = {2, 3, 4, 5, 6, 8};

B B = {2, 4, 6, 8}; (AB)C = {1, 2, 3, 4, 5, 6, 8}; A(BC= {1, 2, 3, 4, 5, 6, 8};

A B = {2, 4}; AC = {3, 4}; BC = {4, 6}; BB= {2, 4, 6, 8}; (AB)C = {4};

A (BC) = {4}.

2.

W ×V ={(Joao, Vera), (Joao, Maria), (Jose, Vera), (Jose, Maria), (Paulo, Vera), (Paulo, Maria)}.

V× W ={( Vera, Joao), (Maria ,Joao,), (Vera ,Jose), (Maria, Jose), (Vera, Paulo), (Maria, Paulo)}.

V × V = {(Vera, Vera), (Vera, Maria), (Maria, Vera), (Maria, Maria)}

5.

a

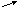
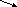
b

d

a

a c

d

a

d

d

a

b

d

a

b c

d

a

d

d

a

b

d

a

c c

d

a

d

d

6.

A × ( B C ) = {(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4)};

b) ( A × B ) ( A ×C ) = {(a, 2), (a, 3), (b, 2), (b, 3), (a, 4), (b, 4)};

c) A × ( B C ) = {(a, 3), (b, 3)};

d) ( A × B ) ( A ×C ) = {(a, 3), (b, 3)}.

7.

(x, y) A × ( BC ) x A y BC y B y C (x, y) A × B (x, y) A × C (x, y) (A × B)( A × C)

(x, y) (A × B)( A × C) (x, y) (A × B) (x, y) (A × C) x A y B y C y BC (x, y) A × ( BC )

8. ( S × W ) ( S × V ) = {(a, 3), (a, 5), (b, 3), (b, 5)}.

9.

a)

(x, y) A × A x A y A x B y B x C y C (x, y) B × B (x, y) C × C (x, y) (B × B)(C × C)

(x, y) (B × B)(C × C) (x, y) B × B (x, y) C × C x B y B x C y C x A y A (x, y) A × A

b)

1. (x, y) A × A 2. x A 3. y A 4. x B 5. y B 6. x C 7. y C 8. (x, y) B × C 9. (x, y) C × B 10.(x, y) (B × C)(C × B)

11. (x, y) (B × C)(C × B) 12. (x, y) B × B 13. (x, y) C × C 14. x B 15. y C 16. x C 17. y B 18. x A 19. y A 20. (x, y) A × A

10.

a) Y 3 1 4 0 X -2	b) Y -2 0 3 X -3
c) Y 2 -3 0 3 X -1	d) Y 2 -3 0 1 X

11.

x A(AB) x A x A(AB)

x A(AB) x A x AB x A(AB) x (AB) x A x AB x A(AB) x A(AB)

12. Usamos aqui o método de prova por contrario. Suponhamos que as condições do problema

cumprem-se, mas C B. Isto significa que existe

pelo menos um x C mas xB. Agora consideremos duas possibilidades: xA e

x A. Se cada alternativa leva a contradição com o enunciado, isto vai significar que a

nossa suposição que C B é falsa.

x A x AC x AB x B - contradição

x A x AC x AB x B - contradição

Todas as igualdades podem ser provadas por meio de diagramas de Wenn a partir das definições da diferença simétrica e do complemento.

Usamos de novo prova por contrario. Suponhamos o contrario, que não é vazio. Então, existe x. x deve ser positivo, porque deve pertencer a cada um dos conjuntos A_nque contem apenas números positivos. Mas para qualquer que seja pequeno positivo x existe n tal quee xA_ne, como consequência, x. Esta contradição diz que a suposição feita é falsa, o conjuntorealmente é vazio.

15.

a)

x C (AB) x AB x A x B x C (A) x C (B) x C (A)C (B)

x C (A)C (B) x C (A) x C (B) x A x B x AB x C (AB)

b)

x C (AB) x (AB) x A x C (A) x C (A)C (B) x B x C (B) x C (A)C (B) x C (A)C (B)

x C (A)C (B) x C (A) x A x (AB) x C (AB) x C (B) x B x (AB) x C (AB) x C (AB)

16.

A B = {1, 2, 3, 5, 7, 9, 11};	b) A C = {3, 5, 7, 11};
c) (A B)Cc= {1, 5, 7, 11} ;	d) A \ B = {1, 9};
e) C \ D = {3, 6, 12};	f) B D = {3, 4, 5, 7, 8, 11}.

17. a) [2, 3]; b) [0, 6]; c) [0, 2); d) [0, 2) (3, 6]; e) (-, 0)(3,) ; f).

18. a) {1, 2, 3, 4, 5, 6, 8, 10}; b) {2, 4}; c) {1, 3, 5, 6, 8, 10}; d) {1, 3, 5, 6, 8, 10};

Текст 6. Як логіка пропозицій використовується при конструюванні та використанні комп’ютерів