
- •1. Ділення на множині цілих чисел.
- •1. Відношення подільності та його властивості.
- •2. Ділення з остачею.
- •3. Задачі:
- •2. Найбільший спільний дільник. Алгоритм евкліда.
- •2. Алгоритм Евкліда.
- •3. Задачі:
- •3. Найменше спільне кратне.
- •4. Прості і складені числа.
- •1. Прості числа і їх властивості.
- •2. Розклад складених чисел на прості множники.
- •5. Нескінченість множини простих чисел. Решето Ератосфена.
- •4.3Адачі:
- •5. Варіанти контрольних робіт.
3. Задачі:
1. Доведіть властивість НСД: якщо кожне з чисел а і b помножити на одне й те ж число к ≠ 0, то їх найбільший спільний дільник помножиться на к.
2. За допомогою алгоритму Евкліда знайдіть НСД чисел:
1)42628 і 33124; 2) 71004 і 154452; 3) 469459 і 519203;
4)179370199 і 4345121; 5) 299, 391, 667; 6) 1955, 2431, 3111, 4862.
3. Найменше спільне кратне.
Означення: Нехай а і b цілі числа, відмінні від 0. Ціле число к називається спільним кратним цих чисел, якщо воно ділиться на а і на b.
Ціле число К називається найменшим спільним кратним чисел а і b, якщо:
1) К—спільне кратне а і b;
2) будь-яке спільне кратне цих чисел ділиться на К.
Позначається К = [а, b] або НСК (а, b).
Теорема:
Число
![]() ,де
(a,b)
– найбільший спільний дільник двох
натуральних чисел a
і
b,
є
найменшим спільним кратним цих чисел.
,де
(a,b)
– найбільший спільний дільник двох
натуральних чисел a
і
b,
є
найменшим спільним кратним цих чисел.
Доведення: Нехай (а,b) = d, тоді а = п∙d, b = 1∙d, де (п,l) = 1. (Поясніть, чому числа п та l — взаємнопрості). Отже
![]()
Ця рівність показує, що
![]() ділиться
на b
і
на a,
тобто є спільним кратним a
і
b.
Покажемо тепер, що будь-яке кратне K>0
чисел a
і
b
ділиться
на
ділиться
на b
і
на a,
тобто є спільним кратним a
і
b.
Покажемо тепер, що будь-яке кратне K>0
чисел a
і
b
ділиться
на
![]() .Оскільки
.Оскільки
![]() то K=a∙s=n∙d∙s.
Крім
того
то K=a∙s=n∙d∙s.
Крім
того
![]() і
b=l∙d,
тому
і
b=l∙d,
тому
![]() ,
а отже
,
а отже
![]() .Оскільки
(n,l)
= 1, то
.Оскільки
(n,l)
= 1, то
![]() ,
отже існує таке число k,
що s=l∙k
.
,
отже існує таке число k,
що s=l∙k
.
Тоді
K=n∙d∙s=n∙d∙l∙k
і
оскільки
![]() ,
то K
ділиться на
,
то K
ділиться на
![]() .
Отже,
.
Отже,
![]() -
найменше спільне кратне чисел a
і
b.
-
найменше спільне кратне чисел a
і
b.
Приклад 1. Знайти [364, 143]. Спочатку знаходимо (364, 143) за алгоритмом Евкліда:
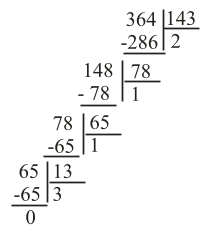
(364, 143)= 13
[364, 143] = (364, 143)/13 = 28∙143 = 4004
Для спрощення знаходження НСК варто знати такі його властивості:
Якщо кожне з чисел а і b помножити або поділити на одне й те ж число m≠0, то їх НСК також помножиться або поділиться на це число m:
1)
[am,
bm]
=
![]()
2)
![]()
Приклад 2. Знайдемо [5640, 2500]. Поділимо кожне число на 10 і знайдемо за допомогою алгоритму Евкліда.
(564, 250) = 2, тоді [564, 250] = (564∙250) / 2 = 564∙125 = 70500. Тоді [5640, 2500] = 70500∙10 = 705000.
Приклад 3. Знайдемо [35, 77, 1141].
![]()
![]()
Отже, [35,77,1141] = 62755.
Задачі:
1. Довести властивості 1), 2) НСК двох чисел.
2. Довести, що НСК двох взаємно простих чисел дорівнює їх добутку.
3. Знайти НСК чисел:
1) 120, 96; 2) 71004, 154452; 3) 232, 460, 280; 4) 67283, 122433, 221703.
4. Прості і складені числа.
1. Прості числа і їх властивості.
Означення: Натуральне число називається простим, якщо воно більше за 1 і не має інших дільників, крім 1 і р.
Натуральне число називається складеним, якщо воно більше за 1 і має, принаймні, один дільник, відмінний від 1 та р.
Число 1 не належить ні до простих, ні до складених чисел. Першими простими числами в натуральному ряді є 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41 ...
Таким чином, множина всіх натуральних чисел розбивається на три підмножини:
1) прості числа, 2) складені числа, 3) число 1.
Основним фактом теорії простих чисел є твердження про те, що будь-яке складене число розкладається і при тому єдиним способом (з точністю до порядку запису) в добуток простих чисел. Перед тим, як довести цю теорему, яка отримала назву "основної теореми арифметики", розглянемо спочатку деякі властивості простих чисел.
1. Якщо просте число ділиться на деяке натуральне п≠ 1, то р = п. (Доведення — методом від супротивного).
2.
Якщо
![]() і
і
![]() —
різні прості числа, то
—
різні прості числа, то
![]() не
ділиться на
не
ділиться на
![]() (Використати означення).
(Використати означення).
3. Будь-яке натуральне число п > 1 ділиться хоча б на одне просте число. (Доведення методом математичної індукції).
4. Якщо п — натуральне число, а р — просте, то або п ділиться на р, або пір — взаємно прості. (Використати найбільший спільний дільник (р, n) ).
5. Якщо добуток двох або більше натуральних чисел ділиться на просте число р, то хоча б один з множників ділиться на р. (Доведення методом математичної індукції).
6. Теорема: Якщо натуральне число п складене, а р його
найменший
простий дільник, то
р
≤![]() .
.
Доведення:
Оскільки
п
—
складене число, а р
—
його найменший простий дільник, то
п=р∙![]() ,
причому
р≤
,
причому
р≤![]() .
Помножимо
обидві частини нерівності на рівні
числа р∙
.
Помножимо
обидві частини нерівності на рівні
числа р∙![]() і
п.
Отримаємо
р2
і
п.
Отримаємо
р2![]() <
<![]() п,
звідки
р2
≤ п, або
р
≤
п,
звідки
р2
≤ п, або
р
≤![]() .
.
Наслідок:
Якщо
число п
не
ділиться на жодне просте число, яке не
перевищує
![]() ,
то n
— просте, в протилежному випадку — воно
складене.
,
то n
— просте, в протилежному випадку — воно
складене.
Приклад:
Нехай
п=137.
11 <![]() <
12. Розглянемо прості числа 2,
3,
5,
7,
11. Число 137 не ділиться на жодне з них,
отже воно є простим.
<
12. Розглянемо прості числа 2,
3,
5,
7,
11. Число 137 не ділиться на жодне з них,
отже воно є простим.
