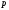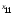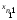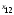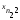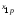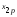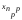- •1. Основные сведения из теории вероятностей и математической статистики
- •1.1. Основные понятия
- •1.2. Законы распределения случайных величин при малом объеме выборки
- •2. Дисперсионный анализ данных наблюдений
- •2.1. Однофакторный дисперсионный анализ
- •Контрольный расчет
- •Оценка влияния отдельных факторов
- •Однофакторный дисперсионный анализ
- •2.2. Двухфакторный дисперсионный анализ
- •Дисперсионный анализ без повторений
- •Дисперсионный анализ с повторениями
- •2.3. Дисперсионный анализ в материаловедении
- •2.4. Дисперсионный анализ в геодезии
- •3. Формирование выборки из выборок малого объема
- •3.1. Проверка однородности независимых выборок
- •3.2. Проверка однородности парных наблюдений
2. Дисперсионный анализ данных наблюдений
2.1. Однофакторный дисперсионный анализ
Методы дисперсионного анализа позволяют формировать единую базу данных объектов-аналогов и оценивать величину влияния конкретных факторных признаков на исследуемый результативный признак.
Основная идея однофакторного дисперсионного анализа заключается в сравнении дисперсии исследуемого признака, вызванной действием фактора, с дисперсией ошибок измерения этого признака. Если различие между ними значимо, то фактор оказывает существенное влияние на исследуемый признак.
Для сравнения влияния факторных признаков на результативный признак необходим определенный статистический материал – каждому уровню фактора должна соответствовать определенная выборка значений результативного признака. Статистический материал удобно представлять в виде таблицы 2.1.
Общее число наблюдений
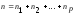 .
.
Прежде чем судить о количественном влиянии фактора, необходимо установить наличие такого влияния. Возможно, расхождение значений результативного признака для различных уровней фактора объясняется действием чистой случайности.
Т а б л и ц а 2.1
Матрица экспериментов для однофакторного анализа
|
Уровни фактора |
Номер выборки | |||
|
1 |
2 |
… |
| |
|
Значения результативного признака |
…
|
…
|
|
…
|
|
Объем выборки |
|
|
|
|
На статистическом языке это предположение означает проверку однородности всех выборок таблицы 2.1, т.е. проверку принадлежности всех значений результативного признака одной генеральной совокупности. Основной процедурой дисперсионного анализа является проверка этой гипотезы с помощью статистических критериев.
Пусть фактор
 имеет
имеет различных уровней, на каждом из которых
выполнено
различных уровней, на каждом из которых
выполнено наблюдений. Следовательно, наблюдалось
наблюдений. Следовательно, наблюдалось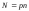 значений
значений признака (свойства)
признака (свойства)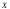 ,
где
,
где - номер наблюдения (
- номер наблюдения ( ),
),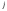 - номер уровня фактора (
- номер уровня фактора (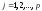 ).
).
Чем существеннее
влияние фактора на признак
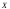 ,
тем сильней будут различаться между
собой средние значения групп наблюдений
на разных уровнях фактора
,
тем сильней будут различаться между
собой средние значения групп наблюдений
на разных уровнях фактора .
.
Существуют понятия:
общая сумма квадратов - сумма квадратов отклонений всех возможных значений признака от их общего среднего значения
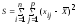 ;
(2.1)
;
(2.1)
сумма квадратов между группами или по факторам - взвешенная сумма квадратов отклонений средних значений по группам от общего среднего значения
 ;
(2.2)
;
(2.2)
сумма квадратов внутри групп - сумма квадратов отклонений возможных значений признака каждой группы (уровня фактора) от среднего значения этой группы
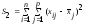 ,
(2.3)
,
(2.3)
где
 - соответственно среднее значение группы
и общее среднее значение результативного
признака, определяемые по формулам
- соответственно среднее значение группы
и общее среднее значение результативного
признака, определяемые по формулам
 .
(2.4)
.
(2.4)
Для оценки влияния фактора следует разложить общую сумму квадратов на составляющие: сумму квадратов между группами (по факторам) и сумму квадратов внутри групп. Следовательно,
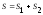 .
(2.5)
.
(2.5)
Сумма
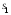 отражает влияние на результативный
признак уровней фактора, а сумма
отражает влияние на результативный
признак уровней фактора, а сумма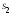 - влияние погрешностей измерений. Так
как
- влияние погрешностей измерений. Так
как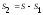 ,
то сумму
,
то сумму называют еще остаточной суммой квадратов.
называют еще остаточной суммой квадратов.
Суммы квадратов
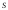 ,
, ,
,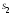 ,
деленные на соответствующие числа
степеней свободы, дают три несмещенные
оценки дисперсии
,
деленные на соответствующие числа
степеней свободы, дают три несмещенные
оценки дисперсии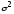 генеральной совокупности:
генеральной совокупности:
 ;
(2.6)
;
(2.6)
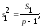 (2.7)
(2.7)
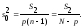 (2.8)
(2.8)
Первая оценка называется общей оценкой дисперсии (или выборочной дисперсией), вторая – оценкой дисперсии по факторам (оценкой дисперсии между группами или факторной дисперсией) и третья – остаточной оценкой дисперсии (оценкой дисперсии внутри групп или остаточной дисперсией).
Число степеней
свободы представляет собой число
независимых отклонений значений признака
от его среднего значения. Сумма
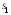 имеет
имеет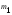 =
= степень свободы, так как из
степень свободы, так как из отклонений групповых средних от общей
средней независимых будет (
отклонений групповых средних от общей
средней независимых будет (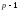 ),
а последнее отклонение выражается через
все предыдущие. Сумма
),
а последнее отклонение выражается через
все предыдущие. Сумма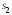 имеет
имеет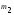 =
=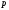 (
(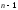 )=(
)=(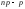 )
степеней свободы, так как вычисляется
по отклонениям
)
степеней свободы, так как вычисляется
по отклонениям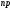 наблюдений от
наблюдений от средних. Число степеней свободы
проверяется путем сложения тем же
способом, что и сумма квадратов (3.5), т.е.
средних. Число степеней свободы
проверяется путем сложения тем же
способом, что и сумма квадратов (3.5), т.е.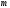 =
=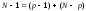 .
.
Если факторная
дисперсия
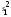 окажется меньше остаточной
окажется меньше остаточной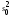 ,
то фактор оказывает несущественное
влияние на признак
,
то фактор оказывает несущественное
влияние на признак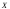 .
.
Проверка значимости
оценок дисперсии выполняется с помощью
 – критерия Фишера, расчетное значение
которого определяется дисперсионным
отношением
– критерия Фишера, расчетное значение
которого определяется дисперсионным
отношением
 =
=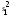 /
/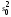 при
при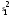 >
>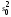 .
(2.9)
.
(2.9)
Если расчетное
значение критерия окажется меньше
критического, то нет оснований считать,
что рассматриваемый фактор влияет на
изменчивость средних значений случайной
величины. Если
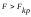 ,
то на принятом уровне значимости делается
вывод о существенном влиянии фактора
,
то на принятом уровне значимости делается
вывод о существенном влиянии фактора на признак
на признак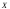 .
.
После того как выполнена оценка влияния фактора на изменчивость средних значений случайной величины в целом и установлено, что фактор влияет на изменчивость средних значений, то переходят к подробному исследованию отдельных уровней фактора. Для этого проводится оценка расхождения средних значений, полученных при наблюдениях по отдельным уровням фактора.
Для сравнения двух
выборочных средних используют
 - статистику. Вычисляют общую дисперсию
двух выборок и расчетное значение
- статистику. Вычисляют общую дисперсию
двух выборок и расчетное значение - статистики по формулам:
- статистики по формулам:
 (2.10)
(2.10)
 .
(2.11)
.
(2.11)
Критическое значение
 - статистики определяется с помощью
статистической функции СТЬЮДРАСПОБР.
Число степеней свободы
- статистики определяется с помощью
статистической функции СТЬЮДРАСПОБР.
Число степеней свободы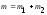 .
Гипотеза о равенстве выборочных средних
подтверждается, если
.
Гипотеза о равенстве выборочных средних
подтверждается, если .
Если
.
Если ,
то уровень фактора с большим средним
значением оказывает существенное
влияние на исследуемый признак.
,
то уровень фактора с большим средним
значением оказывает существенное
влияние на исследуемый признак.
Пример 2.1 [5].
Две группы
дилеров продают автомобили, которые
рекламируются соответственно рекламами
 и
и .
Третья группа дилеров работает без
рекламы. В каждой группе задействовано
по 4 дилера. Таким образом,
.
Третья группа дилеров работает без
рекламы. В каждой группе задействовано
по 4 дилера. Таким образом,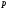 =3,
=3, =4.
В таблице 2.2 приведено количество
автомобилей, которые проданы различными
группами дилеров.
=4.
В таблице 2.2 приведено количество
автомобилей, которые проданы различными
группами дилеров.
Требуется определить влияние двух видов рекламы на объем продаж автомобилей.
Т а б л и ц а 2.2
Сводка исходных данных
|
Дилер |
Реклама А |
Реклама В |
Рекламы нет |
|
1 |
51 |
62 |
42 |
|
2 |
52 |
64 |
48 |
|
3 |
56 |
68 |
50 |
|
4 |
57 |
70 |
52 |
Для пояснения методики однофакторного дисперсионного анализа выполнен контрольный расчет.