67. Основные соотношения, отражающие сущность моб.

Запишем 2 соотношения, кот. явл. основой мат. модели МОБ: 1)если рассмотреть схему по строкам, то можно сделать вывод, что для каждой отрасли производителя вся вал. Продукция распределяется на промежут. потребл-е и кон. исп-ние.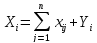, i=1,n (1). Ф-ла (1) представляет собой систему n-ур-ний, кот. назыв. ур-ями распред-ния прод-ции отраслей по направлениям исп-ния. 2)если рассмотреть схему по столбцам, то для каждой отрасли потребителя вал. затраты состоят из промежуточных затрат и ВДС. 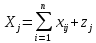, j=1,n (2). Ф-ла (2) также представляет систему n-ур-ний, кот. отражают стоимостной состав прод-ции всех отраслей. Просуммируем (1) и (2) по всем отраслям: 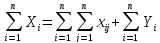,. Из последних двух соотн-ний видно:(3). Ф-ла (3) показывает, что в МОБ соблюдается важнейший принцип единства матер-ого и стоим-ого состава ВВП.

ВВП можно определить 3-мя методами: 1) м-д по конечному исп-нию. Исп-тся данные 2-ого квадранта: У=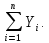2) финансовый м-д. Исп-тся данные 3-его квадранта: У=3) производственный м-д. Отражаются показатели 1-ого квадранта: У=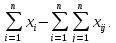

68. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).

Основу МОБ составляет технологическая матрица, кот. состоит из к-тов прямых затрат – мат-ных затрат на произв-во ед-цы прод-ции, кот. рассчитываются по формуле: 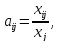i,j=1,n (1). КПЗ показывают какое кол-во прод-ции i-ой отрасли необходимо, если учитывать произв-во ед-цы прод-ции j-ой отрасли. Они не зависят от объема произв-ва в отрасли и явл. довольно стабильной величиной во времени. Исп-зуя ф-лу ,i=1,n, можно записать в виде: Если ввести векторно-матричную запись, то последнюю формулу можно записать в виде:

Х=АХ+У – ЭММ МОБ (модель Леонтьева, модель «затраты-выпуск»).

69. Используя фор-лу х=Ах+у (– модель «затраты-выпуск») можно сделать расчеты: модель Леонтьева

Если в модель будут заданы величины валового продукта каждой отрасли, то можно определить величину конечной продукции каждой отрасли:

У=(Е-А)Х

Где Е – единичная матрица порядка n

Если в модели будут заданы величины конечной продукции, то можно найти объем валового выпуска каждой отрасли:

Обозначим через В

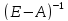- обратная матрица к матрице Е-А. В числителе находится присоединенная матрица Е-А, элементы которой представляют собой алгебраические дополнения для элементов транспонированной матрицы 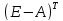. В знаменателе находится определитель матрицы(Е-А).

Элементы матрицы В наз. Коэффициентами полных затрат, кот. показ. , какое ко-во продукции i-ой отрасли нужно произвести , чтобы с учетом прямых и косвенных затрат получить един. Конечной прод. j-ой отрасли.

70. Решени е задачи прогнозирования цен осущ. На основе 1 и 3 квадрата МОБ.

Отрасли-производители	Отрасли-потребители
	1	2	…	n
1	х11	х12	…	х1n
2	х21	х22	…	х2n
…	…	…	…	…
n	хn1	xn2	…	xnn
Промыленные затраты		…	…
Валовая добавленная стоимость	Z1	Z2	…	Zn
Валовые затраты	х1	x2		xn

При этом пол. Соотношение 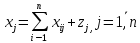. Прогнозирование цен на период t осущ. На основе данных периода t-1. Обозначим индекс роста цен вi-ой отрасли через рi. Тогда в таблице МОБ данные запишутся след. образом

Отрасли-производители	Отрасли-потребители
	1	2	…	n
1	х11p1	х12 p1	…	х1npn
2	х21p2	х22 p2	…	х2n pn
…	…	…	…	…
n	хn1 pn	xn2 pn	…	xnn pn
Валовая добавленная стоимость	Z1 p1	Z2 p2	…	Zn pn
Валовые затраты	х1 p1	x2 p2		xn pn

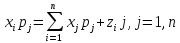С учетом индекса цен фор-ла перепишется ввиде – базовая банковская модель для прогнозирования цен в отраслях