16. Пров стат значимости коэф ур-ния множ лин регрессии

Значим каждого коэфрегрbjопределt-статистикой аналогично парной линейной регр:

tbj=bj/Sbj=;

Sbj-стат ошибка коэфbj,

S^2- необ дисп. Если |tb|>tj-α, n-m, то коэф регрессии bjзначим на уровне α (знач смотр по таблице).

42. Теорема о сведении плат-й матрицы к матрице с полож числами.

Т-ма:Если p* и q* оптим-е смеш-е стр-гии соотв-но игроков А и В в матричной игре 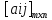и ценой игры V, то эти стр-гии будут оптим-ми и в матричной игреи ценой игры V`=bV+c,b>0.

Док-во: Согласно теор.3 для оптим-й смеш-й стр-гии p* игрока А и для любой чистой стр-гии Bj игрока В вып-ся нер-во: 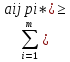V, j=1,n. Умножим посл-е нер-во на полож-е число и обеим частям нер-в прибавим произв-е 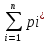, пол-м:+cVb+c+ c. Т.к. =1, то пол-м: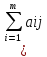b c)pi*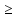bV+c, j=1,n. Т-ма док-на для смеш-й стр-гии p* игрока А. Ан-но q* игрока В. На основании данной теор-мы плат матрицу игры, имеющую отриц числа можно преобразовать в матр-цу с полож числами.

43. Сведение матричной игры к задаче линейного программирования

Пусть имеем матричную игру размерности mxn:

а₁₁ а₁₂ … а_1n

а₂₁ а₂₂ … а_2n

. . . . . . . . . . .

а_m1 а_m2 … а_mn

Обозначим через p*и q*оптимальные смешанные стратегии игроков А и В Оптимальная смешанная стратегия p* игрока A гарантирует ему выигрыш не меньше V независимо от того, какую из чистых стратегий выбирает игрок В

а₁₁p₁*+ а₁₂p₂*+ … + а_1np_m* >=V

а₂₁p₁*+ а₂₂p₂*+ … + а_2np_m* >=V где р_i*>=0, i = 1,m ∑(i=1,m)p_i*=1(1)

. . . . . . . . . . . . . . . . . . . . . .

а_m1p₁*+ а_m2p₂*+ … а_mnp_m* >=V

Оптимальная смешанная стратегия q* гарантирует игроку В проигрыш не больше цены игры V не зависимо от выбора чистой стратегии игроком А

а₁₁q₁*+ а₁₂q₂*+ … + а_1nq_m* <=V

а₂₁q₁*+ а₂₂q₂*+ … + а_2nq_m* <=V где q_j*>=0, j = 1,n ∑(j=1,m)p_j*=1 (2)

. . . . . . . . . . . . . . . . . . . . . .

а_m1q₁*+ а_m2q₂*+ … а_mnq_m* <=V

Cогласно теореме 5 все компоненты платежной матрицы можно сделать положительными, значит V>0 Преобразуем (1) и (2) разделив обе части на V и введем обозначение 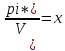_i , i = 1,m , _{j ,} j = 1,n

а₁₁x₁+ а₁₂x₂+ … + а_1nx_m >=1

а₂₁x₁+ а₂₂x₂+ … + а_2nx_m >=1 где x_i>=0, i = 1,m ∑(i=1,m) x_i =1/V (3)

. . . . . . . . . . . . . . . . . . . . . .

а_m1x₁+ а_m2x₂+ … а_mnx_m >=1

Аналогично:

а₁₁y₁+ а₁₂y₂+ … + а_1ny_m >=1

а₂₁y₁+ а₂₂y₂+ … + а_2ny_m >=1 где y_j>=0, j = 1,n ∑(i=1,n) y_j =1/V (4)

. . . . . . . . . . . . . . . . . . . . . .

а_m1y₁+ а_m2y₂+ … а_mny_m >=1

так как игрок А стремится максимизировать цену игры V, то тогда обратная величина 1/V будет минимизироваться, следовательно оптимальная стратегия игрока А находится из задачи

Min f = x₁+x₂+…+x _m ограничения (3)

Аналогично рассуждая оптимальную стратегию игрока В найдем из задачи

Max ψ=y₁+y₂+…+y_n Ограничения (4)

Решив эти задачи мы сможем определить

V=1/f*=1/ ψ*

р_i*=v x_i*, i = 1,m

q_j*= v y_j* , j = 1,n