
- •2. Понятие и виды коррел. И регресс. Задачи коррел. И регресс. Ан-за
- •3. Парн. Лин. Регресс.(плр)
- •5.Коэф-т корреляции
- •6.Предпос. М-да наим. Квадратов. Т. Г-м
- •7.Анализ точности опред. Оценок коэф-ов регрессии.
- •1. Понятие экон-ки. Осн. Задачи экон-ки.
- •8) Проверка гипотез относит. Коэф-тов лин. Ур-я регрес
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •13. Расчет коэф-в множ. Регр-ии.
- •24/Обратная модель.
- •14. Дисперсии и станд. Ошибки коэф-в.
- •19. Проверка равенства двух коэффициентов детерминации.
- •20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок
- •21. Статистика Дарбина-Уртсона
- •22.Логарифмические (лог-линейные) модели.
- •Вопрос 28 – Постановка и мат. Модель задачи векторной оптимизации
- •Вопрос 30 – методы решения многоцелевых задач
- •31. Метод лин.Комбинаций част.Критериев.
- •32. Метод ведущего критерия.
- •34. Метод равных и наим-их относит. Отклонени
- •35. Метод минимакса
- •36. Предмет и основные понятия теории игр
- •40. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
- •41.Теорема о преобразованиях эл-ов платежной матрицы
- •16. Пров стат значимости коэф ур-ния множ лин регрессии
- •42. Теорема о сведении плат-й матрицы к матрице с полож числами.
- •43. Сведение матричной игры к задаче линейного программирования
- •44. Игры с природой. Понятие риска сиатистика. Матрица рисков.
- •45. Критерии Байеса и Лапласа выбора наилучшей стратегии статистика
- •46. Критерии Вальда, Сэвиджа и Гурвица выбора наилучшей стратегии статистика.
- •47. Модели анализа основных финансовых операций.
- •48. Дисконтирование денежных потоков. Текущая стоимость проекта.
- •49. Чистая текущая стоимость инвестиционного проекта
- •50. Внутренняя норма прибыли проекта
- •Вопрос 51. Индекс прибыльности и период окупаемости проекта.
- •Вопрос 52. Влияние инфляции на денежные потоки проекта.
- •55. Осн. Понятия и опр. Спу
- •54.Анализ чувств-ти ден. Потоков проекта
- •17, 18. Проверка общ кач-ва ур множ рег-сии и статзначимостикоэф детерминации.
- •56. Правила построения сет. Графиков
- •57. Расч. Врем. Парам. Событ.
- •Вопрос 60 Оптимизация проекта по времени, если задан срок выполнения проекта
- •Вопрос 59 Линейный график комплекса работ (график Ганта). Диаграмма потребления ресурсов
- •58. Расч времен парам раб.
- •61. Оптимизац проекта по времени за счет вложен выделен сумм.Ср.
- •62. Оптимизация проекта по стоимости при нефиксированной величине критического пути.
- •67. Основные соотношения, отражающие сущность моб.
- •68. Мат. Модель моб. Эк. Сущность коэф-тов прямых затрат (кпз).
- •65.Принципиальная схема моб в снс.
- •66. Экономическое содержание квадрантов моб.
40. Решение матричных игр в смешанных стратегиях. Теорема о необходимом и достаточном условии смешанных стратегий
Смешанной
стратегией игрока А( или B) наз-ся вектор
p=(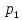 ,
,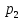 ,..,
,..,
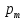 ),
),
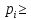 0,i=1,m;
0,i=1,m;
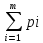 =1
(q=(
=1
(q=(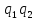 ,…
,… ),
),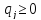 ,j=1,n,
,j=1,n,
 =1).
Т.к. игроки А и B выбирают свои чистые
стр-гии случайно и нез-мо друг от друга,
т.е. игрок А выб.cтр-гию
Аi с вер-тью
=1).
Т.к. игроки А и B выбирают свои чистые
стр-гии случайно и нез-мо друг от друга,
т.е. игрок А выб.cтр-гию
Аi с вер-тью
 ,
а игрок B выб-т стр-гию Bj с вер-ю
,
а игрок B выб-т стр-гию Bj с вер-ю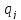 ,
след-но вер-ть комбинации (Аi,Bj)=pi
,
след-но вер-ть комбинации (Аi,Bj)=pi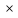 qj.
Зн-т, случ-й будет и вел-на выигрыша
игрока А(проигрыша B). Мы будем вести
речь о ср.вел-не(мат.ожидании), кот-е
явл-ся ф-цией от смешанных стр-гий и
опред-ся по ф-ле: f(p,q)=
qj.
Зн-т, случ-й будет и вел-на выигрыша
игрока А(проигрыша B). Мы будем вести
речь о ср.вел-не(мат.ожидании), кот-е
явл-ся ф-цией от смешанных стр-гий и
опред-ся по ф-ле: f(p,q)=
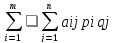
Смешанная
стр-гия наз-ся оптимальной, если для
произв-х стр-гий p=(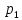 ,
, ,..,
,..,
 ),
q=(
),
q=( ,…
,…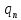 )
вып-ся след. Нер-во f(p,q*)
)
вып-ся след. Нер-во f(p,q*)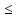 f(p*,q*)
f(p*,q*) f(p*,q)
(1)
f(p*,q)
(1)
Из посл-го нер-ва сл-т, что в седловой точке (p*,q*) платежная ф-ция f(p,q) достигает макс-ма по смеш-м стр-ям p и мин-ма по смеш-м стр-ям q. Знач-я плат-й ф-ции при оптим-х смеш-х стр-гиях и опред-ет цену игры: V=f(p*,q*)
Теорема 2: В смеш-х стр-гиях любая конечная матр-я игра имеет седловую точку.
Теорема
3: Для того, чтобы смеш-е стр-гии p* u q*
игр-в А и B в игре с матрицей [aij] разм-ью
mxn и ценой игры V были оптим-ми необ-мо
и достаточно вып-е нер-в
 pi*
pi*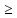 V,
j=1,n
(2)
;
V,
j=1,n
(2)
;
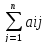 qj*
qj*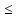 V,
i=1,m
(3)
V,
i=1,m
(3)
Док-во:
пусть p* и q* опт-е смеш-е стр-гии, покажем
что для них будут вып-ся (2) и (3). Восп-ся
опр-ем опт-х смеш-х стр-гий для кот-х
вып-ся ф-ла (1). Запишем ее в развернутой
форме:
 V
V
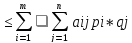 (4)
(4)
В
правую часть (4) подст-м вектор
qj=(0,…,0,1,0,…,0),
получим:
 =
= V.
Что и док-ет, что опт-я смеш-я стр-гия p*
удовл-ет нер-ву (2)
V.
Что и док-ет, что опт-я смеш-я стр-гия p*
удовл-ет нер-ву (2)
Дост-ть:
Пусть вып-ся нер-ва (2) и (3). Докажем, что
p* и q* опт-е смеш-е стр-гии, т.е. имеет
место соотношение (4), док-м, что из нер-ва
(2) след-ют правая часть (4), пусть q=( ,…
,…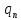 )
– произв-й вектор, тогда:
)
– произв-й вектор, тогда: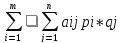 =
=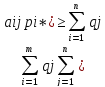 V=V.
V=V.
Итак,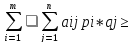 V,
а это и есть правая часть соотн-я (4).
Аналог-но док-ся, что из нер-ва (3) след-т
левая часть соотн-я (4). Т.о. из теоремы
след-т:
V,
а это и есть правая часть соотн-я (4).
Аналог-но док-ся, что из нер-ва (3) след-т
левая часть соотн-я (4). Т.о. из теоремы
след-т:
Если игрок А прим-т свою опт-ю смеш-ю стр-ю p*, а игрок B любую чистую стр Bj, то выигрыш игрока А будет не меньше цены игры V.
Если игрок B прим-т свою любую чистую опт-ю смеш-ю стр q*, а игрок А любую чистую стр Ai, то проигрыш игрока B не превысит цены игры V.
Чистые стр. наз-ся активными.
41.Теорема о преобразованиях эл-ов платежной матрицы
Т-ма: Если один из игроков придерж-ся своей смеш. опт. стр., то его выигрыш ост-ся пост-м и равен цене игры нез-мо от того какую стр-гию прим-т др. игрок, если только тот не выходит за пределы своих активных стр-гий.
Док-во:
Пусть набор (p*,q*,V) явл-ся решением матр-й
игры
 .
При этом игрок А имеет r акт-х стр-гий,
а игрок B имеет k ак-х стр-гий. Планируем
чистые стр-гии игроков так, чтобы ак-е
оказались первыми, получим:p*=(
.
При этом игрок А имеет r акт-х стр-гий,
а игрок B имеет k ак-х стр-гий. Планируем
чистые стр-гии игроков так, чтобы ак-е
оказались первыми, получим:p*=( ,
,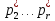 ,0,…,0),
где
,0,…,0),
где ,q*=(
,q*=( ,
,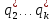 ,0,…,0),
где
,0,…,0),
где .
Пусть игрок А прид-ся своей опт-й смеш-й
стр-гии p*, а игрок B чистой стр-гии. Тогда,
согласно теореме 3 пол-м:
.
Пусть игрок А прид-ся своей опт-й смеш-й
стр-гии p*, а игрок B чистой стр-гии. Тогда,
согласно теореме 3 пол-м: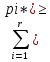 V,
j=1,k
(5)
V,
j=1,k
(5)
Если
игроки А и B исп-т свои опт-е смеш-е
стр-гии, то выигрыш игрока А равен цене
игры , где V= *.
Учит-я нер-во (5) пол-м: V=
*.
Учит-я нер-во (5) пол-м: V=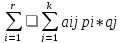 *=
*= *
*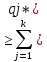 V=V.
Посл. соотношение выполнимо лишь тогда,
когда нер-во (5) превращ-ся в рав-во.
Отсюда можно сделать вывод, что для
любой смеш-й стр-гии q*=(
V=V.
Посл. соотношение выполнимо лишь тогда,
когда нер-во (5) превращ-ся в рав-во.
Отсюда можно сделать вывод, что для
любой смеш-й стр-гии q*=( ,
, ,0,…,0)
будет вып-ся рав-во: V=
,0,…,0)
будет вып-ся рав-во: V=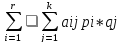 ,что
и док-т теорему.
,что
и док-т теорему.
