
- •Лекция 3.
- •Механические колебания и волны.
- •5.1. Свободные механические колебания (незатухающие и затухающие)
- •5.2. Кинетическая и потенциальная энергии колебательного движения
- •5.3. Сложение гармонических колебаний
- •5.4. Сложное колебание и его гармонический спектр
- •5.5. Вынужденные колебания. Резонанс
- •5.6. Автоколебания
- •5.7. Уравнение механической волны
- •5.8. Поток энергии и интенсивность волны
- •5.9. Ударные волны
- •5.10. Эффект Доплера
5.2. Кинетическая и потенциальная энергии колебательного движения
Кинетическую энергию материальной точки, колеблющейся по гармоническому закону, можно вычислить по известной формуле, используя выражение (5.12):
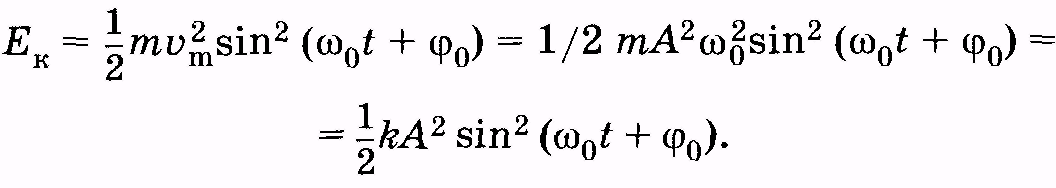 (5.24)
(5.24)
Потенциальную
энергию колебательного движения
найдем, исходя из общей формулы для
потенциальной энергии упругойдеформации
![]() и
используя выражение (5.8):
и
используя выражение (5.8):
![]() (5.25)
(5.25)
Суладывая кинетическую (5.24) и потенциальную (5.25) энергии, получаем полную механическую энергию материальной точки, колеблющейся по гармоническому закону:
 (5.26)
(5.26)
При отсутствии сил трения полная механическая энергия системы не изменяется:
![]() (5.27)
(5.27)
Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 5.8.

5.3. Сложение гармонических колебаний
Материальная точка может одновременно участвовать в нескольких колебаниях. В этом случае, чтобы найти уравнение и траекторию результирующего движения, следует сложить колебания. Наиболее просто выполняется сложение гармонических колебаний. Рассмотрим две такие задачи.
Сложение гармонических колебаний, направленных по одной прямой. Пусть материальная точка одновременно участвует в двух колебаниях, происходящих вдоль одной линии. Аналитически такие колебания выражаются следующими уравнениями:
![]()

![]() тогда результирующее
смещение точки
тогда результирующее
смещение точки
![]()
Выполним такое сложение
с помощью векторной диаграммы.
Изобразим положение
векторов
![]() и
и![]() в начальный
момент времени (рис.
5.9), углы между этими векторами и осью
ОХ равны
начальным фазам слагаемых колебаний
01
и 02.
Вектор
в начальный
момент времени (рис.
5.9), углы между этими векторами и осью
ОХ равны
начальным фазам слагаемых колебаний
01
и 02.
Вектор
![]() — амплитуда
результирующего колебания. Так как
— амплитуда
результирующего колебания. Так как
![]() и
и
![]() вращаютсяс одинаковой угловой
скоростью, то и сумма их — вектор
вращаютсяс одинаковой угловой
скоростью, то и сумма их — вектор
![]() — будет вращаться с той же угловой
скоростью, т. е.
результирующее движение является
гармоническим с круговой частотой
— будет вращаться с той же угловой
скоростью, т. е.
результирующее движение является
гармоническим с круговой частотой![]()
![]() (5.29)
(5.29)
Выразим амплитуду
А
этого колебания и начальную фазу 1
через заданные значения
![]() Применяя теорему косинусов
к треугольнику, заштрихованному на рис.
5.9, получаем
Применяя теорему косинусов
к треугольнику, заштрихованному на рис.
5.9, получаем
![]()
Так как–cos= -cos[- (02 - 01)] = cos (02 - 01), то
![]() (5.30)
(5.30)
Как
видно из рис. 5.9, tg
равен отношению проекции
![]() на ось
OY
к
проекции
на ось
OY
к
проекции
![]() на
ось ОХ,
т. е. Ау
/Ах.
Учитывая,
что проекция
суммы равна сумме проекций, имеем
на
ось ОХ,
т. е. Ау
/Ах.
Учитывая,
что проекция
суммы равна сумме проекций, имеем
 (5.31)
(5.31)
Таким образом, поставленная задача решена: по формулам (5.30) и (5.31) можно найти амплитуду и начальную фазу результирующего колебания. Из выражения (5.30) вытекают следующие частные случаи:
![]()
и тогда
![]()

![]()
тогда
![]()
т. е. амплитуда результирующего колебания равна разности амплитуд слагаемых колебаний, если разность начальных фаз равна нечетному числу (рис. 5.10, б). В частности, при A1 = A2 имеем А = О, т. е. колебания нет (рис. 5.10,в). Это достаточно очевидно: если материальная точка участвует одновременно в двух колебаниях, имеющих одинаковую амплитуду и совершающихся в противофазе, то точка неподвижна. Если частоты складываемых колебаний не одинаковы, то сложное колебание уже не будет гармоническим.
И нтересен
случай, когда частотыслагаемых
колебаний мало отличаются друг от
друга:
нтересен
случай, когда частотыслагаемых
колебаний мало отличаются друг от
друга:![]()
Результирующее колебание при этом подобно гармоническому, но с медленно изменяющейся амплитудой (амплитудная модуляция). Такие колебанияназываются биениями (рис. 5.11).
Сложение взаимно перпендикулярных гармонических колебаний. Пусть материальная точка одновременно участвует вдвух колебаниях: одно направлено вдоль оси ОХ, другое — вдоль оси OY. Колебания заданы следующими уравнениями:
![]() (5.34)
(5.34)
Допустим,
что частоты колебаний одинаковы, т. е.![]() тогда
тогда
![]() (5.35)
(5.35)
Уравнения (5.35) задают траекторию движения материальной точки в параметрической форме. Если в эти уравнения подставлять разные значенияt, то можно определить координатых иу, а совокупность координат и есть траектория. Более наглядно траекторию можно представить в виде зависимостиу = f(x), для получения которой следует исключить время из уравнений (5.35). Произведя математические преобразования, получим уравнение эллипса:
![]() (5.36)
(5.36)
Таким образом, при одновременном участии в двух взаимно перпендикулярных гармонических колебаниях одинаковой частоты материальная точка движется по эллиптической траектории (рис. 5.12).
Из выражения (5.36) вытекают некоторые частные случаи:

Это каноническая форма уравнения эллипса, соответствующая симметричному расположению его относительно осей координат (рис. 5.13, а). Из (5.37) при А1 = А2 = R (рис. 5.13, б) получаем уравнение окружности радиусом R:
![]() (5.38)
(5.38)



![]()
тогда
![]() (5.39)
(5.39)
и после преобразований
![]() (5.40)
(5.40)
Это уравнение прямой линии, в которую вырождается эллипс [рис. 5.14, а соответствует знаку « + » в уравнении (5.40);рис. 5.14, б— знаку «-»].
При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу.
Вид фигур Лиссажу зависит как от соотношения амплитуд А1 и А2, так и от отношения частот 1/2 и разности начальных фаз 01 - 02 слагаемых колебаний (рис. 5.15):


