
- •Елементи теорії поля Тема 15.1. Основні поняття теорії поля
- •Тема 15.2. Скалярне поле
- •15.2.1. Поверхні і лінії рівня
- •15.2.2. Похідна за напрямом
- •15.2.3. Градієнт скалярного поля і його властивості
- •Тема15.3. Векторне поле
- •15.3.1. Векторні лінії поля
- •15.3.2. Потік поля
- •15.3.3. Дивергенція поля. Формула Остроградського – Гаусса
- •15.3.4. Циркуляція поля
- •15.3.5. Ротор поля. Формула Стокса Ротором (або вихором) векторного поля
- •Тема 15.4. Оператор Гамільтона
- •15.4.1. Векторні диференціальні операції першого порядку
- •15.4.2. Векторні диференціальні операції другого порядку
- •1. .
- •Тема 15.5. Деякі властивості основних класів векторних полів
- •15.5.1. Соленоїдальне поле
- •15.5.2. Потенціальне поле
- •15.5.3.Гармонійне поле
15.5.2. Потенціальне поле
Векторне поле
 називаєтьсяпотенціальним
(або
безвихровим,
або градієнтним),
якщо у всіх точках поля ротор дорівнює
нулю, тобто
називаєтьсяпотенціальним
(або
безвихровим,
або градієнтним),
якщо у всіх точках поля ротор дорівнює
нулю, тобто
 .
Прикладом потенціального поля є
електричне поле напруженості точкового
заряду (і інші).
.
Прикладом потенціального поля є
електричне поле напруженості точкового
заряду (і інші).
Наведемо основні властивості потенціального поля.
1.
Циркуляція потенціального поля
 по будь-якому
замкненому контуру в цьому полі дорівнює
нулю.
по будь-якому
замкненому контуру в цьому полі дорівнює
нулю.
Це безпосередньо
випливає з формули (3.14). Отже,
 . Зокрема,
для силового потенціального поля це
означає, що робота сили по будь-якому
замкненому контурі дорівнює нулю; у
полі швидкостей рідини, що тече, рівність
. Зокрема,
для силового потенціального поля це
означає, що робота сили по будь-якому
замкненому контурі дорівнює нулю; у
полі швидкостей рідини, що тече, рівність означає,
що в потоці немає замкнених струйок,
тобто немає водоворотів.
означає,
що в потоці немає замкнених струйок,
тобто немає водоворотів.
2.
У потенціальному полі
 криволінійний
інтеграл
криволінійний
інтеграл
 вздовж будь-якої кривої
вздовж будь-якої кривої з початком у точці
з початком у точці і кінцем у точці
і кінцем у точці залежить тільки від положення точок
залежить тільки від положення точок і
і і не залежить від форми кривої.
і не залежить від форми кривої.

Рис. 15
Ця властивість
випливає з властивості 1. дійсно, взявши
в полі дві точки
 і
і ,
з'єднаємо їх двома кривими
,
з'єднаємо їх двома кривими і
і так, щоб контур
так, щоб контур лежав всередині поля (див. рис. 15)
лежав всередині поля (див. рис. 15)
Тоді, внаслідок властивості 1, маємо
 .
.
Враховуючи властивості криволінійного інтеграла, отримуємо:
 ,
,
тобто
 .
.
3.
Потенціальне поле є полем градієнта
деякої скалярної функції
 ,
тобто якщо
,
тобто якщо ,
то існує функція
,
то існує функція така, що
така, що .
.
З рівності
 випливає, що
випливає, що ,
, ,
, тобто вираз
тобто вираз є повним диференціалом деякої функції
є повним диференціалом деякої функції .
Цю функцію називають потенціалом
векторного поля
.
Цю функцію називають потенціалом
векторного поля ;
; .
.
Звідси:
 ,
, ,
, ,
Отже,
,
Отже,
 ,
,
тобто вектор поля
 є градієнтом скалярного поля.
є градієнтом скалярного поля.
Зауваження.
З рівності
 випливає обернене твердження – поле
градієнта скалярної функції
випливає обернене твердження – поле
градієнта скалярної функції є потенціальним.
є потенціальним.
З рівності
 випливає, що потенціальне поле визначається
заданням однієї скалярної функції
випливає, що потенціальне поле визначається
заданням однієї скалярної функції - його потенціалу. Потенціал векторного
поля може бути знайдений за формулою
- його потенціалу. Потенціал векторного
поля може бути знайдений за формулою
 (5.1)
(5.1)
де
 - координати фіксованої точки,
- координати фіксованої точки, - координати довільної точки. Потенціал
визначається з точністю до довільного
постійного доданку (тому що
- координати довільної точки. Потенціал
визначається з точністю до довільного
постійного доданку (тому що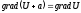 ).
).
Довільне ж векторне
поле вимагає задання трьох скалярних
функцій ( ,
,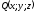 ,
, - проекції вектора поля на осі координат).
- проекції вектора поля на осі координат).
Зауваження.
Означення потенціального поля може
бути дане інакше – векторне поле
 називається потенціальним, якщо воно
є градієнтом деякого скалярного поля,
тобто
називається потенціальним, якщо воно
є градієнтом деякого скалярного поля,
тобто .
(Іноді пишуть
.
(Іноді пишуть ;
знак “мінус” пишуть для зручності,
звичайно векторні лінії направлені
вбік спадання
;
знак “мінус” пишуть для зручності,
звичайно векторні лінії направлені
вбік спадання :
потік рідини направлений туди, де тиск
менший; теплота переміщується від більш
нагрітого місця до менш нагрітого і
т.д.)
:
потік рідини направлений туди, де тиск
менший; теплота переміщується від більш
нагрітого місця до менш нагрітого і
т.д.)
Приклад 5.1. Встановити потенціальність поля

і знайти його потенціал.
○Маємо:
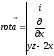

 .
.
Отже, поле вектора
 потенціальне.
потенціальне.
Знайдемо потенціал
 за формулою (5.1), вибравши фіксовану
точку початок координат, тобто
за формулою (5.1), вибравши фіксовану
точку початок координат, тобто .
Тому що
.
Тому що ,
, ,
, ,
то
,
то
 .
●
.
●
15.5.3.Гармонійне поле
Векторне поле
 називаєтьсягармонійним
(або
лапласовим),
якщо воно одночасно є потенціальним і
соленоїдальним, тобто якщо
називаєтьсягармонійним
(або
лапласовим),
якщо воно одночасно є потенціальним і
соленоїдальним, тобто якщо
 і
і .
.
Прикладом гармонійного поля є поле лінійних швидкостей стаціонарного безвихрового потоку рідини при відсутності в ньому джерел і стоків.
Тому що поле
 потенціальне, то його можна записати у
вигляді
потенціальне, то його можна записати у
вигляді ,
де
,
де - потенціал поля.
- потенціал поля.
Але оскільки поле одночасно і соленоїдальне, то
 ,
,
або, що те ж саме,
 ,
,
тобто потенціальна
функція
 гармонійного поля
гармонійного поля є розв’язком диференціального рівняння
Лапласа. Така функція називається, як
уже згадували, гармонійною.
є розв’язком диференціального рівняння
Лапласа. Така функція називається, як
уже згадували, гармонійною.
