Тема 15.4. Оператор Гамільтона

15.4.1. Векторні диференціальні операції першого порядку

Основними диференціальними операціями (діями) над скалярним полем і векторним полемє,,. Дії взяття градієнта, дивергенції і ротора називаютьсявекторними операціями першого порядку (у них беруть участь тільки перші похідні).

Ці операції зручно записувати за допомогою так званого оператора Гамільтона

Цей символічний вектор називають також оператором (читається набла); він набуває визначеного змісту лише в комбінації із скалярними або векторними функціями. Символічне “множення” векторана скалярабо векторвідбувається за звичайними правилами векторної алгебри, а “множення” символів,,на величини ,,,розуміють як знаходження відповідної частинної похідної від цих величин.

Застосування оператора Гамільтона, дає змогу отримати диференціальні операції першого порядку:

1. .

2. .

3. .

Оператор Гамільтона застосовується для запису й інших операцій і для виведення різних формул у теорії поля. При діях з ним треба користуватися правилами векторної алгебри і правилами диференціювання.

Зокрема, похідна за напрямом (4.2) може бути записана у вигляді

,

де .

15.4.2. Векторні диференціальні операції другого порядку

Після застосування оператора Гамільтона до скалярного або векторного поля отримаємо нове поле, до якого можна знову застосувати цей оператор. У результаті отримуємо диференціальні операції другого порядку. Неважко переконатися, що є лише п'ять диференціальних операцій другого порядку: ,,,,.

(Зрозуміло, що операція, наприклад, не має змісту:- скаляр, казати про дивергенцію скаляра, тобто про, безглуздо.)

Запишемо явні вирази для диференціальних операцій другого порядку, використовуючи оператор Гамільтона. Помітимо при цьому, що оператор діє тільки на множник, розташований безпосередньо за оператором.

1. .

Права частина цієї рівності називається оператором Лапласа скалярної функції 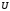і позначається. Таким чином,

. (4.1)

Диференціальне рівняння Лапласа відіграє важливу роль у різних розділах математичної фізики. Розв’язками рівняння Лапласа є так званігармонійні функції.

Зауваження. До рівності (4.1) можна прийти, розглядаючи скалярний оператор дельта:

(який теж називають оператором Лапласа).

2. , тому що векторний добуток двох однакових векторів дорівнює нулю (нуль-вектор). Це означає, що поле градієнта є поле безвихрове.

3.

.

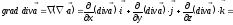
4. , тому що мішаний добуток трьох векторів, з яких два однакові, дорівнює нулю. Це означає, що поле вихря – соленоїдальне.

5. , тому що подвійний векторний добуток має властивість

.

Тут - векторна величина, отримана в результаті застосування оператора Лапласа до вектора.

Тема 15.5. Деякі властивості основних класів векторних полів

15.5.1. Соленоїдальне поле

Нагадаємо, що векторне поле називається соленоїдальним, якщо у всіх точках його дивергенція поля дорівнює нулю, тобто.

Прикладами соленоїдальних полів є: поле лінійних швидкостей твердого тіла обертання (див. приклад 3.4); магнітне поле, створене прямолінійним провідником, уздовж якого тече електричний струм, і інші.

Наведемо деякі властивості соленоїдального поля.

1. У соленоїдальному полі потік вектора через будь-яку замкнуту поверхню дорівнює нулю. Ця властивість безпосередньо випливає з формули (3.8). Таким чином, соленоїдальне поле не має джерел і стоків.

2. Соленоїдальне поле є полем ротора деякого векторного поля, тобто якщо , то існує таке поле, що. Векторназиваютьвекторним потенціалом поля .

Кожну з властивостей 1-2 можна було б взяти, як означення соленоїдального поля.

Доводити властивість 2 не будемо. Відзначимо лише, що обернене твердження – поле ротора векторного поля є соленоїдальним – нами доведене (вище ми показали, що ).

3. У соленоїдальному полі потік вектора через поперечний переріз векторної трубки зберігає постійне значення (називаєтьсяінтенсивністю трубки).

Розглянемо векторну трубку між двома її довільними перерізами і; бічну поверхню трубки позначимо через(див. рис. 14). Потік вектора через замкнуту поверхню, що складається з ,і, дорівнює нулю. Отже,

,

де - зовнішня нормаль.

Тому що на бічній поверхні векторної трубки нормаль перпендикулярна до векторів поля, то і, отже, .

Рис. 14

Змінивши напрямок нормалі на площадки , тобто взявши внутрішню нормаль, отримаємо:

У полі швидкостей рідини, що тече, отриманий результат означає, що кількість рідини, що втікає в трубку за одиницю часу, дорівнює кількості рідини, що витікає з неї.