
- •Елементи теорії поля Тема 15.1. Основні поняття теорії поля
- •Тема 15.2. Скалярне поле
- •15.2.1. Поверхні і лінії рівня
- •15.2.2. Похідна за напрямом
- •15.2.3. Градієнт скалярного поля і його властивості
- •Тема15.3. Векторне поле
- •15.3.1. Векторні лінії поля
- •15.3.2. Потік поля
- •15.3.3. Дивергенція поля. Формула Остроградського – Гаусса
- •15.3.4. Циркуляція поля
- •15.3.5. Ротор поля. Формула Стокса Ротором (або вихором) векторного поля
- •Тема 15.4. Оператор Гамільтона
- •15.4.1. Векторні диференціальні операції першого порядку
- •15.4.2. Векторні диференціальні операції другого порядку
- •1. .
- •Тема 15.5. Деякі властивості основних класів векторних полів
- •15.5.1. Соленоїдальне поле
- •15.5.2. Потенціальне поле
- •15.5.3.Гармонійне поле
15.3.4. Циркуляція поля
Нехай векторне
поле утворене вектором (3.1). Візьмемо в
цьому полі деяку замкнену криву
 і виберемо на ній певний напрямок.
і виберемо на ній певний напрямок.
Нехай
 - радіус-вектор точки
- радіус-вектор точки
 на контурі
на контурі
 .
Відомо, що вектор
.
Відомо, що вектор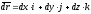 ,
напрямлений по дотичній до кривої в
напрямку її обходу (див.
рис. 10) і
,
напрямлений по дотичній до кривої в
напрямку її обходу (див.
рис. 10) і
 ,
де
,
де - диференціал дуги кривої
- диференціал дуги кривої .
.

Рис. 10
Криволінійний
інтеграл по замкнутому контурі
 від скалярного добутку вектора
від скалярного добутку вектора на вектор
на вектор ,
дотичний до контуру
,
дотичний до контуру ,
називаєтьсяциркуляцією
вектора
,
називаєтьсяциркуляцією
вектора
 вздовж
вздовж
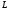 ,
тобто
,
тобто
 .
(3.10)
.
(3.10)
Розглянемо різні форми запису циркуляції. Оскільки
 ,
,
де
 - проекція вектора
- проекція вектора на дотичну
на дотичну ,
проведену в напрямку обходу кривої
,
проведену в напрямку обходу кривої ,
то рівність (3.10) можна записати у вигляді
,
то рівність (3.10) можна записати у вигляді
 ,
(3.11)
,
(3.11)
або
 (3.12)
(3.12)
Циркуляція
 ,
записана у вигляді (3.12) має простий
фізичний зміст: якщо крива
,
записана у вигляді (3.12) має простий
фізичний зміст: якщо крива розташована в силовому полі, то циркуляція
– це робота сили
розташована в силовому полі, то циркуляція
– це робота сили поля при переміщенні матеріальної точки
вздовж
поля при переміщенні матеріальної точки
вздовж .
.
Відзначимо, що
вздовж замкнених векторних ліній
циркуляція відмінна від нуля, тому що
в кожній точці векторної лінії скалярний
добуток
 зберігає знак: додатній, якщо напрямок
вектора
зберігає знак: додатній, якщо напрямок
вектора збігаєтьсяз
напрямком обходу векторної лінії;
від’ємний – у іншому випадку.
збігаєтьсяз
напрямком обходу векторної лінії;
від’ємний – у іншому випадку.
Приклад 3.5.
Знайти
циркуляцію вектора поля лінійних
швидкостей тіла обертання (див.
приклад 1.2)
 вздовж замкненої кривої
вздовж замкненої кривої ,
що лежить у площині
,
що лежить у площині ,
перпендикулярній осі обертання.
,
перпендикулярній осі обертання.
○Будемо вважати,
що напрямок нормалі до площини
 збігається з напрямком осі
збігається з напрямком осі .
Відповідно до формули(3.12), маємо:
.
Відповідно до формули(3.12), маємо:
 ,
,
де
 - площа поверхні, обмежена кривою
- площа поверхні, обмежена кривою .
.
Помітимо, що якщо
нормаль до поверхні
 утворить кут
утворить кут з віссю
з віссю ,
то циркуляція буде рівною
,
то циркуляція буде рівною ;
зі зміною кута
;
зі зміною кута величина
величина змінюється. ●
змінюється. ●
Приклад 3.6.Обчислити циркуляцію векторного поля
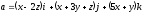
вздовж периметра
трикутника з вершинами
 ,
, ,
, (див. рис. 11).
(див. рис. 11).
○ Відповідно до формули (3.12), маємо:
 .
.
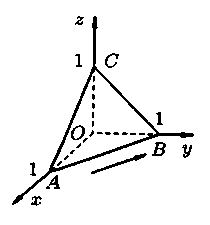
Рис. 11
На відрізку
 :
: ,
, ,
отже,
,
отже,
 .
.
На відрізку
 :
: ,
, ,
отже,
,
отже,

На відрізку
 :
: ,
,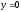 ,
отже,
,
отже,
 .
.
Отже,
 . ●
. ●
15.3.5. Ротор поля. Формула Стокса Ротором (або вихором) векторного поля

називається вектор,
що позначається
 й визначається формулою
й визначається формулою
 (3.13)
(3.13)
Формулу (3.13) можна записати за допомогою символічного визначника у вигляді, зручному для запам'ятовування:


 .
.
Відзначимо деякі властивості ротора.
Якщо
 - постійний вектор, то
- постійний вектор, то .
. , де
, де
 .
. , тобто ротор суми
двох векторів дорівнює сумі роторів
доданків.
, тобто ротор суми
двох векторів дорівнює сумі роторів
доданків.Якщо
 - скалярна функція, а
- скалярна функція, а - векторна, то
- векторна, то
 .
.
Ці властивості легко перевірити, використовуючи формулу (3.13). покажемо, наприклад, справедливість властивості 3:

Використовуючи поняття ротора і циркуляції, векторного поля, запишемо відому в математичному аналізі формулу Стокса:
 . (3.14)
. (3.14)
Ліва частина
формули (3.14) являє собою циркуляцію
вектора
 по контуру
по контуру ,
тобто
,
тобто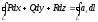 (див.
(3.11)), тобто
(див.
(3.11)), тобто
 .
.
Отже, формулу Стокса можна записати у вигляді

Рис. 12
 .
(3.15)
.
(3.15)
Таке представлення
формули Стокса називають її векторною
формою.
У цій формулі додатній напрямок на
контурі
 і вибір сторони у поверхні
і вибір сторони у поверхні погоджені між собою так само, як у теоремі
Стокса.
погоджені між собою так само, як у теоремі
Стокса.
Формула (3.15) показує,
що циркуляція
вектора
 вздовж замкненого контуру
вздовж замкненого контуру дорівнює потоку ротора цього вектора
дорівнює потоку ротора цього вектора через
поверхню
через
поверхню ,
що лежить у полі вектора
,
що лежить у полі вектора й обмежену контуром
й обмежену контуром (натягнутий
на контур) (див. рис. 12).
(натягнутий
на контур) (див. рис. 12).
Використовуючи формулу (3.14), можна дати інше означення ротора поля, еквівалентне першому і не залежне від вибору координатної системи.
Для цього застосуємо
формулу Стокса (3.15) для досить малої
плоскої площі
 з контуром
з контуром ,
що містить точку
,
що містить точку .
.
За теоремою про середнє для поверхневого інтеграла (властивість 7) маємо:
 ,
,
де
 - якась (середня) точка площі
- якась (середня) точка площі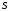 (див.
рис. 13).
(див.
рис. 13).

Рис.13
Тоді формулу (3.15) можна записати у вигляді
 .
.
Звідси:

 .
.
Нехай контур
 стягається в точку
стягається в точку .
Тоді
.
Тоді ,
а
,
а .
Перейшовши до границі отримаємо:
.
Перейшовши до границі отримаємо:
 .
.
Ротором вектора
 в точці
в точці
 називається вектор,
проекція якого на кожний напрямок
дорівнює границі відношенню циркуляції
вектора
називається вектор,
проекція якого на кожний напрямок
дорівнює границі відношенню циркуляції
вектора
 по контуру
по контуру
 плоскої площадки
плоскої площадки ,
перпендикулярної цьому напрямку, до
площі цієї площадки.
,
перпендикулярної цьому напрямку, до
площі цієї площадки.
Як видно з означення,
ротор вектора
 є векторна величина,
що утворює власне векторне поле.
є векторна величина,
що утворює власне векторне поле.
Дамо фізичне
тлумачення поняття ротора векторного
поля. Знайдемо ротор поля лінійних
швидкостей твердого тіла, що обертається
навколо осі
 з постійною кутовою швидкістю (приклад
1.2)
з постійною кутовою швидкістю (приклад
1.2) ,
тобто ротор вектора
,
тобто ротор вектора .
.
За означенням ротора



 .
.
Ротор цього поля напрямлений паралельно осі обертання, його модуль дорівнює подвоєній кутовій швидкості обертання.
З точністю до
числового множника ротор поля швидкостей
 являє собою кутову швидкість обертання
твердого тіла. З цим зв'язана сама назва
“ротор” (лат. “обертання”).
являє собою кутову швидкість обертання
твердого тіла. З цим зв'язана сама назва
“ротор” (лат. “обертання”).
Зауваження.
З означення (3.13) ротора випливає, що
напрямок ротора – це напрямок, навколо
якого циркуляція має найбільше значення
(густину) у порівнянні з циркуляцією
навколо будь-якого напрямку, що не
збігається з нормаллю до площадки
 .
.
Тому зв'язок між ротором і циркуляцією аналогічний зв'язку між градієнтом і похідною за напрямом.
