
- •Елементи теорії поля Тема 15.1. Основні поняття теорії поля
- •Тема 15.2. Скалярне поле
- •15.2.1. Поверхні і лінії рівня
- •15.2.2. Похідна за напрямом
- •15.2.3. Градієнт скалярного поля і його властивості
- •Тема15.3. Векторне поле
- •15.3.1. Векторні лінії поля
- •15.3.2. Потік поля
- •15.3.3. Дивергенція поля. Формула Остроградського – Гаусса
- •15.3.4. Циркуляція поля
- •15.3.5. Ротор поля. Формула Стокса Ротором (або вихором) векторного поля
- •Тема 15.4. Оператор Гамільтона
- •15.4.1. Векторні диференціальні операції першого порядку
- •15.4.2. Векторні диференціальні операції другого порядку
- •1. .
- •Тема 15.5. Деякі властивості основних класів векторних полів
- •15.5.1. Соленоїдальне поле
- •15.5.2. Потенціальне поле
- •15.5.3.Гармонійне поле
15.3.3. Дивергенція поля. Формула Остроградського – Гаусса
Важливою характеристикою векторного поля (5.1) є так звана дивергенція, що характеризує розподіл і інтенсивність джерел і стоків поля.
Дивергенцією (або розбіжністю) векторного поля

у точці
 називається скаляр вигляду
називається скаляр вигляду і позначається символом
і позначається символом ,
тобто
,
тобто
 (3.6)
(3.6)
Відзначимо деякі властивості дивергенції.
Якщо
 - постійний вектор, то
- постійний вектор, то .
. , де
, де
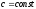 .
. , тобто дивергенція
суми двох векторних функцій дорівнює
сумі дивергенції доданків.
, тобто дивергенція
суми двох векторних функцій дорівнює
сумі дивергенції доданків.Якщо
 - скалярна функція,
- скалярна функція, - вектор, то
- вектор, то .
.
Ці властивості легко перевірити, використовуючи формулу (3.6). Доведемо, наприклад, справедливість властивості 4.
Оскільки
 , то
, то

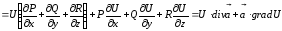 .
.
Використовуючи поняття потоку і дивергенції векторного поля, запишемо відому в аналізі формулу Остроградського – Гаусса
 (3.7)
(3.7)
у так званій векторній формі.
Розглядаючи область
 ,
обмежену замкненою поверхнею
,
обмежену замкненою поверхнею ,
у векторному полі (3.1), можна стверджувати,
що ліва частина формули (3.7) є потік
вектора
,
у векторному полі (3.1), можна стверджувати,
що ліва частина формули (3.7) є потік
вектора через поверхню
через поверхню ;
підінтегральна функція правої частини
формули є дивергенція вектора
;
підінтегральна функція правої частини
формули є дивергенція вектора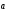 .
Отже, формулу (3.7) можна записати у вигляді
.
Отже, формулу (3.7) можна записати у вигляді
 (3.8)
(3.8)
(у якій вона найчастіше і зустрічається).
Формула
Остроградського-Гаусса означає, що
потік векторного поля через замкнену
поверхню
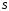 (у
напрямку зовнішньої нормалі, тобто
зсередини) дорівнює потрійному інтегралу
від дивергенції цього поля по об’єму
(у
напрямку зовнішньої нормалі, тобто
зсередини) дорівнює потрійному інтегралу
від дивергенції цього поля по об’єму ,
обмеженому даною поверхнею.
,
обмеженому даною поверхнею.
Використовуючи
формулу (3.8), можна дати інше означення
дивергенції векторного поля
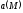 в точці
в точці (не зв'язане з вибором координатних
осей).
(не зв'язане з вибором координатних
осей).
За теоремою про середнє для потрійного інтеграла маємо:
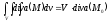 ,
,
де
 - деяка (середня) точка області
- деяка (середня) точка області .
Тоді формулу (3.8) можна переписати у
вигляді
.
Тоді формулу (3.8) можна переписати у
вигляді .
Звідси
.
Звідси
 .
.
Нехай поверхня
 стягується в точку. Тоді
стягується в точку. Тоді ,
і ми отримаємо вираз для
,
і ми отримаємо вираз для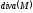 в точці
в точці :
:
 .
(3.9)
.
(3.9)
Дивергенцією
векторного поля
в точці
 називається
границя відношення потоку поля через
(замкнену) поверхню
називається
границя відношення потоку поля через
(замкнену) поверхню ,
що оточує точку
,
що оточує точку ,
до об’єму тіла, обмеженого цією поверхнею,
за умови, що вся поверхня стягується в
точку
,
до об’єму тіла, обмеженого цією поверхнею,
за умови, що вся поверхня стягується в
точку .
.
Означення (3.9) дивергенції еквівалентно (можна показати) означенню (3.6).
Як видно з означення, дивергенція векторного поля в точці є скалярною величиною. Вона утворює скалярне поле в даному векторному полі.
Виходячи з фізичного
змісту потоку (звичайно умовно вважають,
що
 є поле швидкостей фіктивного стаціонарного
потоку нестискаючої рідини), можна
сказати, що: при
є поле швидкостей фіктивного стаціонарного
потоку нестискаючої рідини), можна
сказати, що: при точка
точка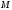 являє собою джерело, звідки рідина
витікає, при
являє собою джерело, звідки рідина
витікає, при точка
точка є сток, що поглинає рідину. Як випливає
з рівності (3.9), величина
є сток, що поглинає рідину. Як випливає
з рівності (3.9), величина характеризує потужність (інтенсивність,
щільність) або джерела, або стоку в точці
характеризує потужність (інтенсивність,
щільність) або джерела, або стоку в точці .
У цьому полягає фізичний зміст дивергенції.
.
У цьому полягає фізичний зміст дивергенції.
Зрозуміло, що якщо
в об’ємі
 ,
обмеженому замкненою поверхнею
,
обмеженому замкненою поверхнею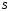 ,
немає ні джерел, ні стоків, то
,
немає ні джерел, ні стоків, то .
.
Векторне поле, у
кожній точці якого дивергенція поля
дорівнює
 ,
тобто
,
тобто ,
називаєтьсясоленоїдальним
(або
трубчастим).
,
називаєтьсясоленоїдальним
(або
трубчастим).
Приклад 3.4.
Знайти дивергенцію поля лінійних
швидкостей
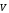 рідини, що обертається як тверде тіло
навколо нерухомої осі із сталою кутовою
швидкістю
рідини, що обертається як тверде тіло
навколо нерухомої осі із сталою кутовою
швидкістю .
.
○ Приймемо за вісь
обертання рідини вісь
 .
Тоді, як показано раніше (див.
приклад 3.2),
.
Тоді, як показано раніше (див.
приклад 3.2),
 .
Маємо:
.
Маємо:
 .
.
Поле
 – соленоїдальне.●
– соленоїдальне.●
