15.2.3. Градієнт скалярного поля і його властивості

У якому напрямку похіднамає найбільше значення? Цей напрямок вказує вектор, який називається градієнтом скалярного поля.

Можна помітити, що права частина рівності (2.2) являє собою скалярний добуток одиничного вектора і деякого вектора.

Вектор, координатами якого є значення частинних похідних функцій у точці, називаєтьсяградієнтом функції і позначають , або.

Відзначимо, що є векторна величина. Кажуть: скалярне полепороджує векторне поле градієнта. Тепер рівність (2.2) можна записати у вигляді

,

або

(2.3)

де - кут між векторомі напрямком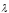(див. рис. 3).

З формули (2.3) відразу випливає, що похідна за напрямом досягає найбільшого значення, коли , тобто при. Таким чином, напрямок градієнта збігається з напрямком, вздовж якого функція (поле) змінюється швидше всього, тобто градієнт функції вказує напрямок найшвидшого зростання функції. Найбільша швидкість зміни функціїу точцідорівнює

Рис. 3

.

У цьому полягає фізичний зміст градієнта. На зазначеній властивості градієнта засноване його широке застосування в математиці й інших дисциплінах.

Наведемо важливі властивості градієнта функції.

1. Градієнт напрямлений по нормалі до поверхні рівня, що проходить через дану точку.

Дійсно, по будь-якому напрямку вздовж поверхні рівня . Але тоді з (24.3) випливає, що, тобто.

2. ,

3. ,

4. ,

5. ,

6. .

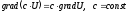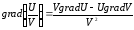Доводяться ці властивості на підставі означення градієнта. Доведемо, наприклад, останню властивість. Маємо:

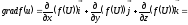
Зауваження. Наведенні властивості градієнта функції залишаються справедливими і для плоского поля.

Приклад 2.2. Знайти найбільшу швидкість зростання функції в точці.

○Маємо: ;

.

Найбільша швидкість зростання функції дорівнює

.

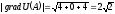Відзначимо, що функція буде спадати з найбільшою швидкістю , якщо точкарухається в напрямку(антиградієнтний напрямок). ●

Тема15.3. Векторне поле

15.3.1. Векторні лінії поля

Розглянемо векторне поле, що задається вектором . Вивчення поля зручно починати з поняття векторних ліній; вони є найпростішими геометричними характеристиками поля.

Векторною лінією поля 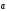називається лінія, дотична, до якої в кожній її точці має напрямок відповідного їй вектора.

Це поняття для конкретних полів має зрозумілий фізичний зміст. Наприклад, у полі швидкостей рідини, що тече, векторними лініями будуть лінії, по яких рухаються частки рідини (лінії потоку); для магнітного поля векторними (силовими) лініями будуть лінії, що виходять з північного полюса і закінчуються в південному.

Сукупність усіх векторних ліній поля, що проходять через деяку замкнену криву, називаються векторною трубкою.

Вивчення векторного поля починають з вивчення розташування його векторних ліній. Векторні лінії поля

(3.1)

описуються системою диференціальних рівнянь виду

. (3.2)

Рис.4

Дійсно, нехай – векторна лінія поля,– радіус-вектор точок. Тодінаправлений по дотичній до лініїв точці(див. рис. 4).

В наслідок колінеарності векторів івипливає пропорційність їхніх проекцій, тобто рівності (3.2).

Приклад 3.1.Знайти векторні лінії поля лінійних швидкостей тіла, що обертається з постійною кутовою швидкістю навколо осі.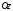

○ Це поле визначене вектором (див. приклад 1.2). Згідно (3.2), маємо:

або

Інтегруючи, отримаємо: тобто векторні лінії даного поля являють собою кола з центрами на осі, що лежать у площинах, перпендикулярних до цієї осі. ●