
- •Елементи теорії поля Тема 15.1. Основні поняття теорії поля
- •Тема 15.2. Скалярне поле
- •15.2.1. Поверхні і лінії рівня
- •15.2.2. Похідна за напрямом
- •15.2.3. Градієнт скалярного поля і його властивості
- •Тема15.3. Векторне поле
- •15.3.1. Векторні лінії поля
- •15.3.2. Потік поля
- •15.3.3. Дивергенція поля. Формула Остроградського – Гаусса
- •15.3.4. Циркуляція поля
- •15.3.5. Ротор поля. Формула Стокса Ротором (або вихором) векторного поля
- •Тема 15.4. Оператор Гамільтона
- •15.4.1. Векторні диференціальні операції першого порядку
- •15.4.2. Векторні диференціальні операції другого порядку
- •1. .
- •Тема 15.5. Деякі властивості основних класів векторних полів
- •15.5.1. Соленоїдальне поле
- •15.5.2. Потенціальне поле
- •15.5.3.Гармонійне поле
Елементи теорії поля Тема 15.1. Основні поняття теорії поля
Теорія поля – великий розділ фізики, механіки, у якому вивчаються скалярні, векторні, тензорні поля.
До розгляду скалярних і векторних полів приводить багато задач фізики електротехніки, математики, механіки й інших технічних дисциплін. Вивчення одних фізичних полів сприяє вивченню й інших. Так, наприклад, сили всесвітнього тяжіння, магнітні, електричні сили – усі вони змінюються обернено пропорційно квадрату відстані від свого джерела; дифузія в розчинах відбувається за законами, спільними з поширенням тепла в різних середовищах; вигляд силових магнітних ліній нагадує картину обтікання перешкод рідиною та ін.
Математичним ядром теорії поля є такі поняття, як градієнт, потік, потенціал, дивергенція, ротор, циркуляція й інші. Ці поняття важливі й у засвоєнні основних ідей математичного аналізу функцій багатьох змінних.
Полем називається
область
 простору, у кожній точці якої визначено
значення деякої величини. Якщо кожній
точці
простору, у кожній точці якої визначено
значення деякої величини. Якщо кожній
точці цієї області відповідає певне число
цієї області відповідає певне число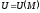 ,
кажуть що в області задано (визначено)скалярне
поле
(або функція
точки).
Інакше кажучи, скалярне поле – це
скалярна функція
,
кажуть що в області задано (визначено)скалярне
поле
(або функція
точки).
Інакше кажучи, скалярне поле – це
скалярна функція
 разом з її областю визначення. Якщо ж
кожній точці
разом з її областю визначення. Якщо ж
кожній точці області простору відповідає деякий
вектор
області простору відповідає деякий
вектор ,
то кажуть, що задановекторне
поле
(або векторну
функцію точки).
,
то кажуть, що задановекторне
поле
(або векторну
функцію точки).
Прикладами скалярних полів можуть бути поля температури (повітря, тіла, …), атмосферного тиску, густини (маси, повітря, …), електричного потенціалу і т.д. Прикладами векторних полів є поле сили тяжіння, поле швидкостей частинок рідини, що тече (вітру), магнітне поле, поле густини електричного струму і т.д.
Якщо функція

 не залежить
від часу, то скалярне (векторне) поле
називається стаціонарним
(або тим, що
встановилося); поле, що змінюється з
часом (змінюється, наприклад, скалярне
поле температури при охолодженні тіла),
називається
нестаціонарним
(або тим, що
не встановилося).
Далі будемо
розглядати лише стаціонарні поля. Якщо
не залежить
від часу, то скалярне (векторне) поле
називається стаціонарним
(або тим, що
встановилося); поле, що змінюється з
часом (змінюється, наприклад, скалярне
поле температури при охолодженні тіла),
називається
нестаціонарним
(або тим, що
не встановилося).
Далі будемо
розглядати лише стаціонарні поля. Якщо
 – область тривимірного простору, то
скалярне поле
– область тривимірного простору, то
скалярне поле
 можна розглядати як функцію трьох
змінних
можна розглядати як функцію трьох
змінних
 (координат
точки
(координат
точки
 ):
):
 (1.1)
(1.1)
(Поряд з позначеннями
 ,
,
 ,
використовують запис
,
використовують запис
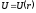 ,
де
,
де
 - радіус-вектор точкиМ.)
- радіус-вектор точкиМ.)
Якщо скалярна
функція
 залежить тільки від двох змінних,
наприклад
залежить тільки від двох змінних,
наприклад і
і ,
то відповідне скалярне поле
,
то відповідне скалярне поле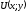 називають
плоским.
називають
плоским.
Аналогічно: вектор
 ,
що визначає векторне поле, можна
розглядати як векторну функцію трьох
скалярних аргументів
,
що визначає векторне поле, можна
розглядати як векторну функцію трьох
скалярних аргументів
 і
і :
: (або
(або
 ).
).
Вектор
 можна подати (розклавши його по ортах
координатних осей) у вигляді
можна подати (розклавши його по ортах
координатних осей) у вигляді
 ,
,
де
 ,
,
 ,
, – проекції вектора
– проекції вектора
 на осі координат. Якщо в вибраній системі
координат
на осі координат. Якщо в вибраній системі
координат
 одна з проекцій вектора
одна з проекцій вектора
 дорівнює нулю, а дві інші залежать тільки
від двох змінних, то векторне поле
називається
плоским.
Наприклад:
дорівнює нулю, а дві інші залежать тільки
від двох змінних, то векторне поле
називається
плоским.
Наприклад: .
.
Векторне поле
називається
однорідним,
якщо
 – постійний вектор, тобто
– постійний вектор, тобто і
і
 – сталі величини. Таким полем є полетяжіння.
Тут
– сталі величини. Таким полем є полетяжіння.
Тут
 ,
,
 ,
,
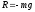 ,
,
 –прискорення
сили ваги,
–прискорення
сили ваги,
 – маса точки.
– маса точки.
Надалі будемо
припускати, що скалярні функції ( – визначають скалярне поле,
– визначають скалярне поле, ,
,
 і
і
 – які задають векторне поле) неперервні
разом з своїми частинними похідними.
– які задають векторне поле) неперервні
разом з своїми частинними похідними.
Приклад 1.1.
а)Функція
 визначає скалярне поле в точках простору,
обмеженого сферою з центром в початку
координат (в кулі) і радіусом
визначає скалярне поле в точках простору,
обмеженого сферою з центром в початку
координат (в кулі) і радіусом .
.
б)Скалярне поле
 визначене у всьому просторі, за винятком
точок осі
визначене у всьому просторі, за винятком
точок осі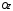 (на ній
(на ній ).
).
Приклад 1.2.
Знайти поле лінійної швидкості
 матеріальної
точки
матеріальної
точки
 ,
що обертається проти годинникової
стрілки з кутовою швидкістю
,
що обертається проти годинникової
стрілки з кутовою швидкістю
 навколо осі
навколо осі
 .
.
Кутову швидкість
подамо у вигляді вектора
 ,
що лежить на осі
,
що лежить на осі
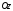 ,напрямленого
вгору. Маємо:
,напрямленого
вгору. Маємо:


 .
.
Побудуємо радіус
вектор
 точкиМ
(див.
рис.1)
точкиМ
(див.
рис.1)
Числове значення
лінійної швидкості
 (модуль),
як відомо з курсу фізики, дорівнює
(модуль),
як відомо з курсу фізики, дорівнює ,
де
,
де - відстань точки обертання
- відстань точки обертання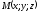 від осі обертання (осі
від осі обертання (осі ).
Але
).
Але (
( - кут між вектором
- кут між вектором і віссю
і віссю
 ).
Отже,
).
Отже,
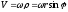 ,
тобто
,
тобто .
.
Вектор швидкості
 направлений
убік обертання, збігаєтьсяз
напрямком векторного добутку
направлений
убік обертання, збігаєтьсяз
напрямком векторного добутку
 (
( , вектори
, вектори утворять праву трійку). Отже,
утворять праву трійку). Отже, ,
тобто
,
тобто


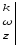
 або
або
 .
.
Поле лінійних
швидкостей
 тіла, що обертається навколо нерухомої
осі, є плоске векторне поле.
●
тіла, що обертається навколо нерухомої
осі, є плоске векторне поле.
●
