Тема 2.2 Физические основы термодинамики

Работа, совершаемая идеальным газом в различных процессах. Внутренняя энергия системы как функция состояния.

Работа и теплопередача. Количество теплоты. Эквивалентность количества теплоты и работы.

Прочитать §81, 82, 83.

Первое начало термодинамики и его применение к изопроцессам. Уравнения и графики этих процессов. Теплоемкость идеальных газов в зависимости от процесса.

Адиабатический процесс. Уравнение Пуассона.

Прочитать §88, 90.

Дополнение. Уместно сразу дать определение мольной (или молярной) теплоемкости.

это скалярная физическая величина, равная тому количеству теплоты, которое необходимо сообщить одному молю вещества или газу, чтобы повысить его температуру на один градус (или отвести это количество теплоты, чтобы понизить его температуру на один градус), т.е.

, (4)

где число молей;

количество теплоты, переданное молям вещества для нагревания наградусов.

Из первого начала термодинамики

.

После почленного деления на , получим, с учетом (4):

и так как (гдечисло степеней свободы), то

. (5)

Откуда хорошо видно, что мольная теплоемкость газов зависит не только от его рода (), но и от процесса, в котором он участвует. Так, например, при(изобарный процесс)

и тогда

или (уравнение Майера),

где мольная теплоемкость газа при постоянном объеме.

Тема 2.3 Второе начало термодинамики

Круговые, обратимые и необратимые процессы. Принцип действия тепловой и холодильной машин. Идеальная тепловая машина Карно и ее КПД.

Прочитать §81, 104 (формулы с энтропией опустить), §106.

Тема 2.4 Структура и свойства твердых тел

Кристаллические и аморфные тела. Кристаллическая решетка. Понятие о характере теплового движения в твердых телах. Теплоемкость и теплопроводность твердых тел. Закон Дюлонга и Пти.

Ознакомиться (§110, 114).

Примеры решения задач

Задача 2.1 В баллоне объемом л находится гелий под давлениемМПа и при температуреК. После того, как из баллона выпустилиг гелия, температура в баллоне понизилась доК. Определить давлениегелия, оставшегося в баллоне.

Д а н о: С И	Р е ш е н и е
л, МПа, К, К, гкг, , .	Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа: , (1) где масса гелия в конечном состоянии; масса одного кмоля гелия; универсальная газовая постоянная. Из уравнения (1) выразим искомое давление : . (2)

Массу гелия выразим через массу, соответствующей начальному состоянию, и массу гелия, выпущенного из баллона

. (3)

Массу гелия найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию

. (4)

Подставляя в выражение (3) массу по формуле (4), а затем полученное выражениев формулу (2), найдем

,

или после преобразования и сокращения

.

Проверка наименования размерности, полученного результата:

.

Вычисление:

МПа.

О т в е т: МПа.

Задача 2.2 Баллон содержит г кислорода иг аргона. Давление смесиМПа, температураК. Принимая данные газы за идеальные, определить емкостьбаллона и плотностьсмеси.

Д а н о: С И	Р е ш е н и е
МПа, К, гкг, гкг, , , .	В соответствии с законом Дальтона: давление смеси газов, не вступающих в химическую реакцию между собой, равно сумме парциальных давлений газов, входящих в состав смеси. Парциальным давлением газа называется давление, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью. Из уравнения Менделеева-Клапейрона парциальные давления кислорода и аргонавыражаются формулами:

и .

Следовательно, по закону Дальтона, давление смеси газов

или ,

откуда емкость баллона равна:

. (1)

Проверим единицу размерности полученного результата:

.

.

После подстановки числовых значений в формулу (1) и произведя вычисления, получим .

Плотность смеси, с учетом (1), равна:

. (2)

После проверки единицы размерности и произведя вычисления, найдем, что .

О т в е т: ,.

Задача 2.3 Вычислить удельные теплоемкости при постоянном объеме и при постоянном давлениинеона и водорода, принимая эти газы за идеальные.

Д а н о: С И	Р е ш е н и е
; , (газ одноатомный), , , (газ двухатомный), .	Удельные теплоемкости идеальных газов выражаются формулами: , (1) , (2) где число степеней свободы молекул газа; масса одного киломоля.

Подставляя числовые значения (1) и (2), получим:

а) для неона:

;

;

б) для водорода:

;

;

О т в е т: для неона: ,;

для водорода: ,.

Задача 2.4 Кислород массой кг занимает объеми находится под давлениемМПа. Газ был нагрет сначала при постоянном давлении до объема, а затем при постоянном объеме до давленияМПа. Найти изменениевнутренней энергии газа, совершенную им работуи теплоту, переданную газу. Построить график процесса.

Д а н о: С И	Р е ш е н и е
кг, , , , Па, Па, .	Изменение внутренней энергии газа выражается формулой: , (1) где число степеней свободы молекул газа (для двухатомных молекул кислорода); масса одного киломоля. Начальную и конечную температуру газа найдем, используя уравнение Клапейрона-Менделеева: . (2) Решая его относительно , получим:

. (3)

Рис. 2.1

Проверим единицу размерности :

.

Выполним расчет температур по формуле (3) для трех точек (1, 2, 3), приведенных на рис. 2.1:

К;

К;

К.

Подставляя в выражение (1) числовые значения, входящих в него величин, и выполняя арифметические действия, находим:

Дж.

Работа расширения газа при постоянном давлении выражается формулой:

.

Подставив числовые значения, получим:

Дж.

Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. . Следовательно, полная работа, совершенная газом, равна:

Дж.

Согласно первому началу термодинамики теплота , переданная газу, равна сумме изменения внутренней энергиии работы:

,

следовательно,

Дж = 3,64 МДж.

График процесса приведен на рис. 2.1.

О т в е т: Дж,Дж,МДж.

Задача 2.5 В цилиндре под поршнем находится водород массой кг при температуреК. Водород сначала расширился адиабатически, увеличив свой объем враз, а затем был сжат изотермически, причем объем газа уменьшился враз. Найти температуру в конце адиабатического расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.

Д а н о: С И	Р е ш е н и е
, , кг, , К, раз, раз, .	Температуры и объемы газа, совершающего адиабатический процесс, связаны между собой соотношением: или , (1) где отношение теплоемкостей газа при постоянном давлении и постоянном объеме (для водорода как двухатомного газа): .

Из соотношения (1) имеем:

.

Подставляя числовые значения заданных величин, находим

К.

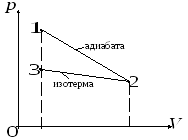
Рис. 2.2

Работу газа при адиабатическом процессе найдем из первого начала термодинамики:

, (2)

так как процесс протекает без теплообмена с окружающей средой.

Из (2) следует, что

. (3)

Проверим единицу размерности искомой величины:

Дж.

Подставив в (3) числовые значения, получим:

Дж.

Работа газа при изотермическом процессе может быть выражена в виде:

или ,

где .

Подставляя известные числовые значения величин, входящих в правую часть этого равенства, и выполняя арифметические действия, находим

Дж.

Знак «минус» показывает, что при сжатии газа работа совершается над газом внешними силами. График процесса приведен на рис. 2.2.

О т в е т: К,Дж,Дж.