Примеры решения задач

Задача 1.1 Найти момент инерции блока радиусом см, а также силы натяженияинитей, перекинутых через блок, к которым прикреплены грузыг иг, если грузопускается за времяс от начала движения на расстояниесм.

Д а н о: С И	Р е ш е н и е
г=кг, г=кг, с, см= 0,9 м	1) Для решения задачи воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для чего укажем какие силы действуют на блок и на каждое тело в отдельности (рис. 1.2). На блок действуют три силы: сила реакции опоры со стороны оси блока, компенсирующая силу тяжести, действующую на блок и силы упругости нитейи.

На груз – сила тяжестии сила упругости; на груз– сила тяжестии сила упругости нити. Учтем, что в соответствии сIII Законом Ньютона и.

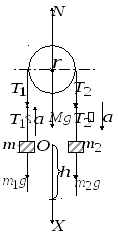
Рис. 1.2

2) Спроецируем эти силы на ось , которую направим вертикально вниз и запишем уравнения движения (II Закон Ньютона) в проекциях на эту ось:

• для первого груза: ; (1)

• для второго груза: ; (2)

где - ускорение грузов.

3) Под действием двух моментов сил иотносительно осиО, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение , где- тангенциальное ускорение точек на ободе блока, равное ускорению грузов.

Из основного уравнения динамики вращательного движения находим искомый момент инерции блока:

. (3)

4) Кинематическое уравнение движения применительно ко второму грузу в координатной форме дает:

. (4)

Откуда получаем, что

.

Подставляя найденное ускорение в (1) и (2), находим:

, (5)

. (6)

Произведем проверку размерности единиц измерения искомых величин:

,

=1 Н,

.

Вычисления:

,

Н,

Н,

.

О т в е т: Н,Н,.

Задача 1.2 Маховик в виде сплошного цилиндра радиусом м и массойкг раскручен до частоты вращенияи предоставлен самому себе. Под действием сил трения от тормозящей колодки маховик остановился черезс. Найти тормозящий момент силы трения.

Д а н о: С И	Р е ш е н и е
м, кг, , , с	Решим эту задачу двумя способами: а) Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде: , (1) где - изменение момента импульса, вращающегося маховика относительно осиО, совпадающей с геометрической осью маховика за интервал времени ;

- искомый момент внешней силы – силы трения, действующей на маховик относительно той же оси.

Рис. 1.3

Момент силы трения неизменен с течением времени по условию задачи, поэтому после интегрирования уравнения (1), получим:

,

откуда

. (2)

Момент инерции маховика в виде сплошного диска, как известно, определяется по формуле:

.

Изменение угловой скорости выразим через конечнуюи начальнуючастоты вращения, пользуясь соотношением

,

.

Подставив в формулу (2) найденные выражения и, получим

. (3)

Выполним проверку размерности единицы измерения искомой величины в СИ:

.

Произведем вычисления, подставляя числовые значения в расчетную формулу (3):

.

Знак «минус» указывает на то, что момент силы трения направлен против направления вращения маховика.

О т в е т: .

б) С точки зрения закона сохранения и превращения механической энергии – вся кинетическая энергия вращательного движения маховика расходуется на работу против силы трения:

. (4)

Так как , то

,

где - начальная угловая скорость маховика.

Таким образом,

,

откуда

,

т.е. получили то же значение величины искомого момента силы трения, что и в пункте а).

Итак, при решении различных задач предпочтение необходимо отдавать законам сохранения и превращения энергии, не говоря уже о том, что многие задачи вообще невозможно решить без этого закона.

Решим еще одну аналогичную задачу.

Задача 1.3 Вал в виде сплошного цилиндра радиуса и массойделает, после действия тормозной колодки, вал, сделавоборотов, остановился. Определить величину средней силы трения останавливающей вал.

Д а н о: С И	Р е ш е н и е
, ,	Согласно закону сохранения и превращения механической энергии, имеем: ,

откуда

.

Это решение еще раз подтверждает, что предпочтение следует отдавать законам сохранения энергии.

Задача 1.4 Горизонтальная платформа в виде сплошного диска массой кг и радиусомм вращается с угловой скоростьюоколо вертикальной оси без трения. С какой угловой скоростью будет вращаться платформа, если человек массойкг перейдет с края платформы в точку, находящуюся на расстоянииот центра платформы и какую работу совершит человек при этом переходе. Момент инерции человека рассчитывать как для материальной точки.

Д а н о: С И	Р е ш е н и е
кг, м, кг, , , .	Так как силы тяжести, действующие на человека и платформу параллельны вертикальной оси, то момент внешних сил относительно этой оси вращения О (рис. 1.4), совпадающей с геометрической осью платформы, равен нулю, поэтому момент импульса системы платформа-человек останется постоянным , или ,

где - момент инерции платформы и человека до его перехода, равный;

-момент инерции платформы и человека после перехода, равный ;

- угловая скорость платформы до перехода;

- искомая угловая скорость после перехода.

Рис. 1.4

Таким образом,

. (1)

Момент инерции платформы (сплошного диска) относительно оси О при переходе человека не меняется, а момент инерции человека – да:

, .

Из (1) искомая величина угловой скорости равна

,

т.е.

.

После проверки размерности в СИ, убедитесь, что .

Вычисление:

.

Работу, совершенную человеком при переходе, найдем из теоремы об изменении кинетической энергии системы платформа-человек

,

где .

Для нашего случая:

.

И тогда

. (2)

Из полученной формулы видно, что размерность искомой величины получается в 1Дж.

Подставляя числовые значения в (2), получим искомый ответ:

Дж

О т в е т: ,Дж.

Задача 1.5 На краю неподвижной горизонтальной платформы, имеющей форму сплошного диска радиусом м стоит человек. Масса платформыкг, масса человекакг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением на оси платформы, найти с какой угловой скоростью будет вращаться платформа, если человек начнет идти вдоль ее края со скоростьюотносительно платформы. Момент инерции человека рассчитывать как для материальной точки.

Д а н о: С И	Р е ш е н и е
м, кг, кг, .	В соответствии с законом сохранения момента импульса для системы платформа-человек, запишем: , (1) где - момент инерции платформы; - момент инерции человека;

- искомая угловая скорость платформы относительно системы отсчета связанной с условно неподвижной Землей;

- угловая скорость человека относительно Земли.

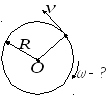
Рис. 1.5

Для того, чтобы найти (задана его линейная скорость относительно платформы), воспользуемся классическим законом сложения скоростей:

,

или, в скалярной форме (с учетом направления движения)

.

Здесь принято за положительное направление – направление движения платформы (рис. 1.5). С учетом, что , расчетная формула принимает вид:

.

Откуда

.

Проверка размерности в СИ дает.

Вычисления:

.

О т в е т: .