4. Постоянный электрический ток

Основные законы и формулы, используемые в решении задач этой темы таковы.

Электрический ток характеризуется силой (величиной) тока

для постоянного тока, (4.1)

мгновенное значение силы тока (4.2)

и плотностью тока

. (4.3)

Плотность силы тока зависит от концентрации свободных носителей зарядов заряженных частиц и скорости их направленного движения

. (4.4)

Согласно закону Ома для однородного участка цепи (участка не содержащего источника тока)

, (4.5)

где падение напряжения на этом участке цепи;

электрическое сопротивление этого участка, равное

. (4.6)

По закону Ома в дифференциальной форме:

, (4.7)

где плотность силы тока;

удельная проводимость проводника;

удельное сопротивление проводника.

В случае металлических проводников величины илинейно зависят от температуры, т.е.

,, (4.8)

где ,значения приС;

термический коэффициент сопротивления .

По закону Ома замкнутой цепи:

, (4.9)

где электродвижущая сила источника (ЭДС).

Для цепи с последовательным соединением проводников

;;. (4.10)

Согласно закону Ома для неоднородного участка цепи

. (4.11)

Знак «плюс» перед берем, когда выбранное направление тока совпадает со стрелкой над источником, а «минус» наоборот, т.е. когда«противодействует» разности потенциалов.

Если между концами проводника имеется разность потенциалов и по проводнику протекает ток постоянной силы, то работа, совершаемая электрическим полем (которую принято называть работой тока) за время, равна

, (4.12)

или, с учетом закона Ома для однородного участка цепи

, (4.13)

. (4.14)

Электрическая мощность постоянного тока определяется формулами

, (4.15)

, (4.16)

. (4.17)

Очень важно помнить, что если формулы (4.12, 4.14 и 4.17) применимы к любому участку цепи и позволяют вычислять полную работу и мощность тока на этих участках, то формулы (4.13) и (4.17) – лишь на однородном участке цепи. Формула (4.13) применима как для однородного участка цепи, так и для неоднородного участка цепи. В последнем случае она позволяет вычислять лишь ту часть работы сил электрического поля, которая идет на преодоление электрического сопротивления этого участка цепи и связанное с этим выделение на этом участке Ленц-Джоулева количества теплоты:

.

По формуле (4.12) вычисляется полная работа тока, так что в общем случае, в соответствии с законом сохранения энергии, имеем

,

где механическая работа или другая, но не электрической природы.

Таким образом, работа силы тока в общем случае расходуется на преодоление электрического сопротивления участка цепи и связанное с этим выделение Ленц-Джоулева тепла и на работу, которая превращается в механическую или химическую энергии.

Что касается работы и мощности источника тока, то они соответственно равны:

, (4.18)

, (4.19)

где ЭДС источника.

Рассмотрим примеры решения задач на расчет цепей постоянного электрического тока.

Задача 4.1.1 Через сопротивление МОм разряжается конденсатор емкостью в 2 мкФ. Определить через какое время от начала разрядки напряжение на пластинах конденсатора уменьшится вдвое.

Д а н о: С И	Р е ш е н и е
МОм = Ом; 2 мкФ = Ф; .	При разрядке конденсатора в цепи появится ток, сила которого равна .

Знак «минус» показывает, что речь идет об убыли силы тока с течением времени; заряд конденсатора, равный

,

где электроемкость конденсатора.

С учетом закона Ома для однородного участка цепи , поэтому

или

.

После интегрирования этого выражения, получим

.

Откуда

,

где инапряжения на конденсаторе, соответствующие началу разрядки конденсатора и времени.

Проверка размерности:

.

Вычисление

с.

О т в е т: с.

Задача 4.1.2 Последовательно с сопротивлением Ом соединены два источника сВ,В и внутренним сопротивлениемОм иОм. Найти показания вольтметра, подключенного к зажимам первого источника. Определить также значение сопротивления, при котором вольтметр показывает нуль. Током через вольтметр пренебречь.

Д а н о: С И	Р е ш е н и е
Ом; В; В; Ом; Ом.	По закону Ома для неоднородного участка цепи (рис. 4.1). . Откуда . (1)

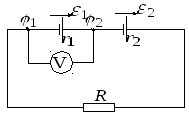
Рис. 4.1

Сила тока в цепи (в соответствии с законом Ома для замкнутой цепи) равна

. (2)

Подставляя значение силы тока из (2) в (1), получим

. (3)

Расчеты дают (с учетом проверки размерности):

В.

Знак «минус» указывает на то, что .

Определим теперь внешнее сопротивление , при котором вольтметр показывать нуль. Для этого случая формула (3) принимает вид

.

Откуда

.

Отметим, что хотя ток в цепи есть, разности потенциалов между точками 1 и 2 – нет.

Расчеты и проверка размерности дают:

Ом.

О т в е т: В;Ом.

Задача 4.1.3 К сопротивлению Ом подсоединены параллельно два элементаВ,Ом иОм. ТокА (рис. 4.2). Найти силу токови,, а также направления токаи.

Д а н о: С И	Р е ш е н и е
Ом; В; Ом; Ом; А.	Выберем произвольное направление тока в схеме, например, как показано на рис. 4.2. Так как , (1) то с учетом закона Ома для неоднородных участков цепи ии закона Ома для однородного участка цепи, формулу (1) можно переписать (принимая, чтои) так:

. (2)

Рис. 4.2

С учетом того, что

,

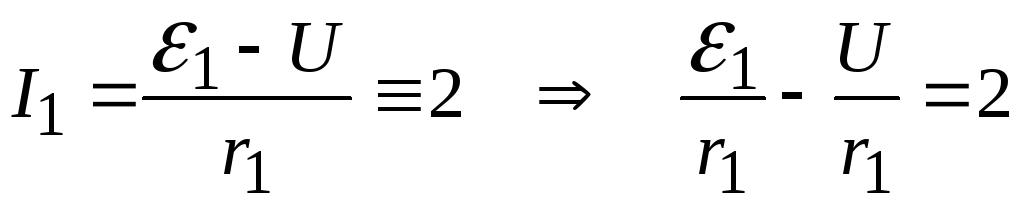следует, что и, следовательно, через сопротивлениеток не идет (!), что противоречит условию. Это означает, что на самом деле направление токавыбрано нами неверно, и поэтому его следует изменить на противоположное направление (рис. 4.3).

Рис. 4.3

В этом случае (с учетом ) приходим к следующему расчету:

,

,

откуда

В.

Так что

А,

А,

,

откуда

В.

Итак, мы получили, что: А;А;В. Этот результат не содержит выше указанных противоречий и поэтому является решением задачи. Правильное направление тока указано на рис. 4.3.

Задача 4.1.4 Батарея с В может дать максимальную силу тока в 10 А. Определить максимальное количество теплоты, которое выделяется в 1 с во внешней цепи и соответствующую плотность тепловой мощности, если подводящие провода сделаны из никелина и имеют поперечное сечение 1.

Д а н о: С И	Р е ш е н и е
В; А; ; .	Закон Ома для замкнутой цепи . (1) Сила тока будет максимальной при условии, что (короткое замыкание), следовательно

. (2)

откуда

. (3)

В соответствии с законом Джоуля-Ленца, количество теплоты, выделяющееся во внешней цепи за время , равно

. (4)

Или с учетом (1)

. (5)

Величина максимальна при таком значении(,), при котором

. (6)

Следовательно,

.

Откуда

.

Таким образом,

Вт.

Для плотности тепловой мощности , имеем:

.

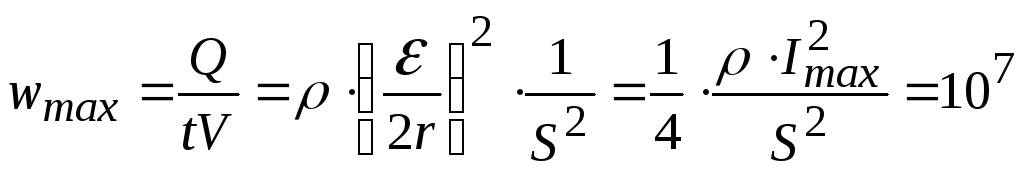
О т в е т: ;Вт.

Задача 4.1.5 Имеется гальванометр, рассчитанный на предельный ток силой 0,5 А. Подсоединив к нему шунт сопротивлением Ом, увеличили предел его измерения в 10 раз. Найти сопротивление гальванометра. Какое добавочное сопротивление надо подсоединить к гальванометру, чтобы использовать его в качестве вольтметра измеряющего напряжение до 25 В?

Д а н о: С И	Р е ш е н и е
А; ; Ом; В.	Для измерения силы тока гальванометр подключают последовательно к сопротивлению измеряемого участка. Для расширения пределов измерения силы тока, к гальванометру (амперметру) подсоединяют параллельно дополнительное сопротивление (шунт). Из рис. 4.4 хорошо видно, что

,

откуда

.

Рис. 4.4

При измерении на пределе шкалы максимального тока силой через гальванометр течет ток силой

,

а через шунт ток силой

,

тогда

и .

Вычисления дают: Ом.

Гальванометр, используемый в качестве вольтметра, подсоединяют параллельно к сопротивлению измеряемого участка. При этом падение напряжения на гальванометр не должно превышать предельного значения

.

Избыточное напряжение

должно падать на последовательно с вольтметром включение дополнительное сопротивление (добавочное) (рис. 4.5)

Рис. 4.5

.

Вычисление и проверка размерности дают: Ом.

О т в е т: Ом; Ом.

Задача 5.1.1 В чистом атмосферном воздухе у поверхности Земли находится около 1000 пар ионов в каждом куб. см. Найти удельное сопротивление воздуха, если подвижность положительных ионов составляет 1,4, а отрицательных 1,6. Считать, что ток далек от насыщения.

Д а н о: С И	Р е ш е н и е
; ; .	По закону Ома в дифференциальной форме , (1)

где плотность тока проводимости;

искомое удельное сопротивление;

напряженность электрического поля;

удельная электропроводность.

С другой стороны, плотность тока может быть определена по формуле

, (2)

где модуль заряда иона, равный элементарному заряду;

число ионов в единице объема;

скорость установившегося равномерного движения ионов, которая связана с напряженностью электрического поля зависимостью

. (3)

Здесь подвижность положительных ионов. Аналогично, для отрицательных

. (4)

Подставив (3) и (4) в (2), получим

. (5)

Тогда из (1) и (5) искомое удельное сопротивление равно

.

Проверка размерности:

.

Вычисление:

.

О т в е т: .