3. Движение заряженных частиц в электрическом поле

Отдельная группа задач посвящена движению заряженных частиц в электрическом поле. Полагая, что заряженная частица не испытывает никаких воздействий, кроме как со стороны сил электрического поля (как правило, речь идет о таких частицах как электрон, протон и др., масса которых весьма мала и силой тяжести действующих на них можно пренебречь в сравнении с силой электрического поля) большинство задач решается с помощью закона сохранения энергии.

Энергия заряженной частицы в электрическом поле складывается из кинетической энергии ее движения и потенциальной энергии ее взаимодействия с электрическим полем, т.е.

,

здесь ипотенциалы точек поля, между которыми происходит перемещение частицы, аиее скорости в этих точках.

Двигаясь вдоль линий напряженности электрического поля (в этом направлении потенциал поля убывает), положительно заряженная частица увеличивает свою кинетическую энергию (при ,) и, наоборот, тормозится встречным полем.

Если, в частности, , то

.

В случае однородного поля разность потенциалов в последнем выражении может быть найдена с помощью формулы

.

Задача 3.3.1 Электрон движется между обкладками плоского конденсатора, заряженного до напряжения 200 В. Расстояние между обкладками 2 см. Какую скорость получит электрон, переместившись на 0,5 мм вдоль линии напряженности, если в начале этого перемещения его скорость м/с. Найти время этого перемещения и ускорение электрона.

Д а н о: С И	Р е ш е н и е
см = 0,02 м; м/с; мм = м; Кл; кг; В.	В соответствии с законом сохранения энергии , откуда искомая скорость равна , здесь изменение потенциала на участке перемещения равно

.

Таким образом,

.

Проверка размерности и вычисления дают окончательный результат:

м/с.

В виду однородности поля () электрон движется с постоянным ускорением

.

Вычисление

.

Искомое время найдем из определения средней скорости

с.

Обратите внимание на то, что ускорение электрона в электрическом поле . Так что, действительно, в подобных задачах силой тяжести можно пренебречь.

О т в е т: м/с;;с.

Задача 3.3.2 Два электрона находясь на бесконечно большом расстоянии друг от друга начинают двигаться навстречу друг другу с одинаковой начальной скоростью км/с. На какое минимальное расстояние они сблизятся?

Д а н о: С И	Р е ш е н и е
км/с = м/с; Кл.	На бесконечном удалении друг от друга электроны обладают лишь кинетической энергией (потенциальной энергией их взаимодействия на таком расстоянии пренебрегаем).

Сблизившись на минимальное расстояние – расстояние, на котором их скорости обращаются в нуль, они обладают лишь потенциальной энергией их взаимодействия в электрическом поле друг друга. Следовательно, в соответствии с законом сохранения энергии можно записать

,

где

,

потенциальная энергия их взаимодействия;

.

Откуда

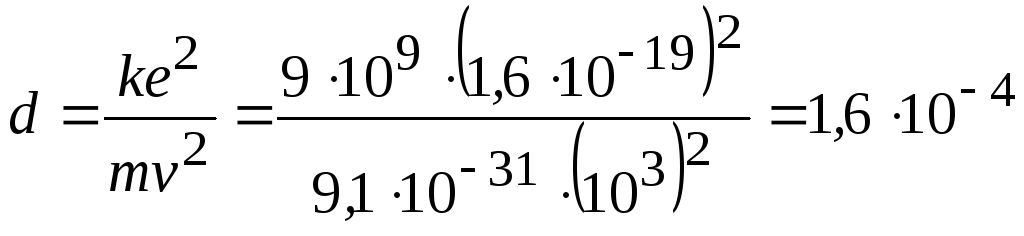м.

О т в е т: м.

Задача 3.3.3 Пучок электронов, ускоренных разностью потенциалов в 40 В, влетает посередине между обкладками плоского конденсатора, параллельно его пластинам. При каком минимальном напряжении электроны не вылетят из конденсатора? Длина обкладок конденсатора см, расстояние между нимисм.

Д а н о: С И	Р е ш е н и е
В; см = 0,1 м; см = 0,02 м.	Из условия задачи вытекает, что силой тяжести, действующей на электроны, можно пренебречь по сравнению с силой электрического поля.

Сделаем чертеж, на котором укажем силу, действующую на электрон со стороны электрического поля конденсатора, начальную скорость электрона при входе в конденсатор и оси координат (как показано на рис. 3.8).

Рис. 3.8

В виду однородности электрического поля конденсатора ,и.

Кинематические уравнения движения в координатной форме, применительно к условию задачи, дают

,

,

где , а начальная скорость электронов

.

Решая эти уравнения совместно, получим (с учетом проверки размерности)

В.

О т в е т: В.