Примеры решения задач к теме

8.3 Дифракция света Основные формулы и методические указания

1. Радиусы зон Френеля для сферической поверхности световой волны, испускаемой точечным изотропным источником , определяется формулой:

, (8. 3. 3)

где – радиус внешней границы‑той зоны;

– радиус волновой поверхности;

– расстояние от вершины волновой поверхности до точки наблюденияР, для которой построены зоны Френеля.

2. Для дифракции в параллельных лучах от одной щели положение минимумов освещенности на экране определяется углом от нормали к плоскости щели и удовлетворяющим условие

,

где – ширина щели;

– длина световой волны;

– порядок минимумов.

При нормальном падении света на дифракционную решетку положение главных максимумов интенсивности света определяется углами , от нормали плоскости решетки и выражаются формулой

,, (8. 3. 4)

где – постоянная (период) решетки, равная расстоянию между серединой двух соседних щелей;

— порядок соответствующего максимума.

В явлении дифракции света волны огибают оптические неоднородности на пути распределения света. Попадая на экран, волны дают распределение интенсивности света на нем вследствие интерференции.

В случае дифракции в параллельных лучах от одной щели для максимумов интенсивности света на экране не существует столь простого соотношения, как (8.3.2), определяющая положение дифракционных минимумов. Иногда пишут формулу

где – угол соответствующий дифракционному максимуму–ого порядка.

Однако, эта формула неточная: она дает завышенные значения для угла . Так ошибка придлясоставляет около 5%, при увеличенииошибка убывает.

Решение задач

З а д а ч а  8. 3. 1 На непрозрачную пластину с круглым отверстием (дифракция Френеля) радиуса мм падает нормально параллельный пучок монохроматического света снм. На пути лучей, проходящих через отверстие, помещен экран, на котором наблюдается дифракционная картина. При каком минимальном расстоянии между пластиной и экраном, превышающем 20 см, в центре экрана будет наблюдаться темное пятно?

Дано: СИ м; м; м.	Решение Расстояние , при котором в центре дифракционной картины будет наблюдаться темное пятно, определяется числом зон
-?	Рис. 8.6

Френеля, укладывающихся в отверстие: если число зон – четное, то в центре – темное пятно. Если в отверстие укладываетсязон Френеля (рис. 8.6), то расстояние от центра экрана 0 до края отверстия набольше, чем расстояние между центром экрана и центром отверстия –.

Теорема Пифагора дает (см. рис. 8.6)

или

.

Выражение и им можно пренебречь, поэтому

и(1)

Так как значение должно быть четным,, то значения, при которых в центре экрана будет темное пятно соответственно равны

м, м,

м, м.

Последнее расстояние (при) меньше 20 см и поэтому не удовлетворяет условию задачи. Прионо будет еще меньше. Следовательно, искомым минимальным расстоянием будет значение(при)м.

Ответ: м.

З а д а ч а  8. 3. 2 Между точечным монохроматическим источником света с мкм и экраном поместили диафрагму с круглым отверстием радиусамм. Расстояние от диафрагмы до источника и экрана равны соответственном им. Как изменится интенсивность света в точке Р, если диафрагму убрать?

Дано: СИ	Решение
м; м; м; м.	Рис. 8. 7	В результате дифракции света на краях отверстия диафрагмы и интерференции вторичных волн на экране возникнут чередующие темные и светлые кольца.
-?

В зависимости от числа зон Френеля, укладывающихся в поверхности волнового фронта радиуса , ограниченного краями отверстия, в центре экрана (в точке Р) будет темное или светлое пятно. Четному числу зон Френеля соответствует темное пятно, нечетному – светлое. Найдем это число.

Полагая в формуле (8.3.3) величину равной радиусу, получим

.

Следовательно, в точке Р – светлое пятно.

Далее заметим, что в силу иколебания светового вектора Е, приходящие в точку Р от каждой из трех зон Френеля имеют приблизительно одинаковые амплитуды. При этом колебания, приходящие от любых двух соседних зон, будучи в противофазе, гасят друг друга и весь эффект сводится к действию всего лишь одной зоны, например, первой. И поскольку, когда диафрагма отсутствует, то действие всей волны равно половине действия первой зоны Френеля. Следовательно, изъятие диафрагмы приведет к уменьшению амплитуды световых колебаний в точке Р в два раза. Так как интенсивность света пропорциональна квадрату амплитуды световых колебаний, то она уменьшится в четыре раза.

Ответ: .

З а д а ч а  8. 3. 3 На прямоугольную щель нормально к ее плоскости падает параллельный пучок монохроматического света (дифракция Фраунгофера); расположенная за щелью линза с фокусным расстоянием м проецирует на экран дифракционную картину в виде чередующихся светлых и темных полос. Ширина центральной светлой полосысм. Как надо изменить ширину щели, чтобы центральная светлая полоса заняла весь экран (при любой ширине)?

Дано: СИ м; м.	Решение Рис. 8. 8
-?

Изображенная на рис. 8.8 кривая показывает распределение интенсивности света на экране.

Центральная светлая полоса на экране заключена между двумя минимумами первого порядка. Ее ширина зависит от угла, соответствующего минимуму первого порядка. Уголсвязан с ширинойформулой (8.3.4), где. И так как при изменении ширины щели отдо, и остаются постоянными, то из (8.3.4) следует:

, (1)

где и– углы соответствующие первым дифракционным минимумам, которые соответствуют размерам щелии.

Так как угол весьма мал (из условия задачи), то. Для того, чтобы центральная полоса занимала весь экрандолжен стремиться к 90°, так что .

Следовательно, с учетом сказанного, из (1) находим

.

Таким образом, ширину щели следует уменьшить в 80 раз.

Ответ: .

З а д а ч а  8. 3. 4 На дифракционную решетку нормально к ее поверхности падает свет от газоразрядной трубки, наполненной гелием. Под углом совпадают красная (м) и голубая (м) линии. Определить максимальный порядок красной линии () в спектре этой решетки, если главное фокусное расстояние собирающей линзы, проектирующей спектр на экранм, а границами видимого спектра испускания гелия являются фиолетовая см и красная см линии. Чему равно расстояние(в мм) между спектрами первого и второго порядков на экране?

Дано: СИ ; м; м; м; м; м.	Решение Рис. 8.9
-? -?

1) Прежде всего необходимо найти постоянную дифракционной решетки , которую можно рассчитать, зная номера спектров красной или голубой линий, совпадающих между собой. Условием совпадения является равенство углов, под которыми видны эти линии в перекрывающихся спектрахIII и IV порядка, и следовательно

Þ .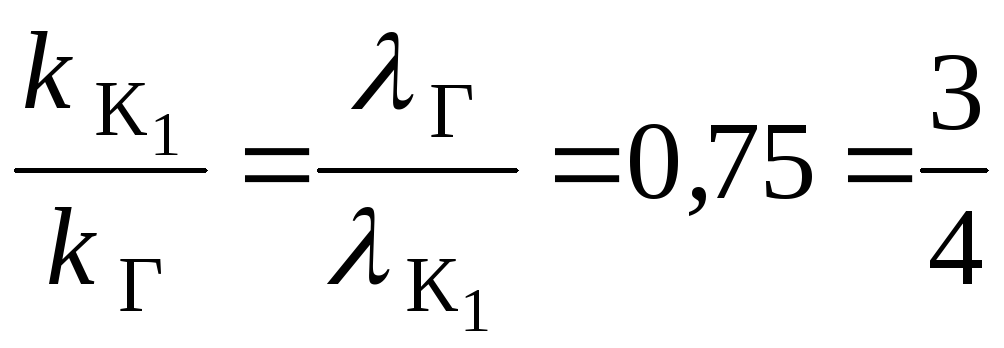

Значит ;.

Таким образом

м.

2) Из основной формулы дифракционной решетки найдем максимальный порядок красной линии (м):

,

откуда

.

Так как – может быть только целым числом, то, для, что невозможно. Следовательно, в спектре испускания гелия с помощью данной решетки можно наблюдать пять порядков линий красного цвета см.

3) Для определения расстояния между спектрами 1-го и 2-го порядков найдем углы в спектре 1-го порядка ив спектре 2-го порядка (границ спектров):

Þ

Þ

Искомое расстояние (рис. 8.9) между спектрами 1-го и 2-го порядков равно

ммм.

Ответ: ,мм.

З а д а ч а  8. 3. 5 На дифракционную решетку нормально к ее поверхности падает параллельный пучок монохроматических лучей с м. Период решетким. Определить число главных минимумов, которое дает эта решетка, а также максимальный уголотклонения лучей, соответствующих последнему дифракционному максимуму.

Дано: СИ м; м.	Решение Из основной формулы дифракционной решетки (8.3.5), определяющей положение главных максимумов интенсивности света следует, что при и
-? -?

Но – целое число, следовательнонадо округлить до целого числа. Округлить донельзя, так как при этом окажется, что, чего быть не может. Поэтому округляем до.

Таким образом, по обе стороны от центрального максимума, которому соответствует , будет наблюдаться поглавных максимумов. Так что, число главных максимумов, которое дает эта решетка (включая центральный) равно

.

Максимальное значение угла найдем из условия (8.3.5), полагая в нем:

откуда .

Ответ: ,.