Примеры решения задач к теме

8.2. Интерференция света Основные формулы и методические указания

1. Оптическая длина пути, проходимого световым лучом в однородной среде с показателем преломления n

(8. 2. 4)

где l - геометрическая длина пути светового луча.

2. Оптическая разность хода двух световых лучей

(8. 2. 5)

3. Условия возникновения максимума и минимума интенсивности света от 2-х когерентных источников соответственно

(8. 2. 6)

и

(8. 2. 7)

где l - длина световой волны в вакууме,

- порядок соответствующего максимума или минимума интенсивности света.

4. Положение на экране (от его центра) последовательно расположенных максимумов и минимумов интенсивности света соответственно

(8. 2. 8)

и

(8. 2. 9)

где .

5. Расстояние между интерференционными полосами на экране, полученными от двух когерентных источников света

(8. 2. 10)

где - расстояние от экрана до источников,

- расстояние между когерентными источниками, причем

6. Оптическая разность хода световых лучей, отраженных от двух поверхностей тонкой пластины или пленки, по обе стороны которых одинаковые среды

(8. 2. 11)

где - толщина пластины или пленки,

- показатель их преломления,

- угол преломления,

- длина световой волны в вакууме.

7. Условия образования максимумов и минимумов интенсивности света в отраженном свете от тонкой плоскопараллельной пластины или пленки соответственно:

(8. 2. 12)

и

(8. 2. 13)

где - угол падения светового луча на пластину или пленку.

8. Радиусы темных и светлых колец Ньютона в отражении света соответственно, при условии, что между линзой и пластиной вакуум (воздух)

(8. 2. 14)

(8. 2. 15)

Здесь - радиус кривизны поверхности линзы, соприкасающейся с параллельной пластиной,- длина световой волны в среде между линзой и пластиной,- порядковый номер кольца (соответствует центральному темному пятну).

Задачи на интерференцию света делятся в основном на две группы: на интерференцию волн от двух когерентных источников и на интерференцию в тонких пластинах (пленках). К задачам первой группы относятся случаи интерференции, получаемые с помощью щелей Юнга (опыт Юнга), зеркала Ллойда, зеркал Френеля, а также бипризмы Френеля. Для расчета интерференционной картины в этом случае используются формулы (8.2.7), (8.2.8) и (8.2.9), предварительно определив (если это необходимо) положение двух когерентных источников. Вторую группу составляют задачи на интерференцию как в плоскопараллельных, так и в клинообразных тонких слоях, а так же задачи на кольца Ньютона. В этом случае соотношение (8.2.10) позволяет вычислить оптическую разность 2-х интерферирующих лучей, отраженных от обеих поверхностей слоя. По условиям (8.2.11) и (8.2.12) определяют результат интерференции.

При интерференции света, известной под названием колец Ньютона, роль тонкой пленки играет прослойка (обычно воздушная) между пластиной и выпуклой поверхностью прижатой к ней линзы. Формулы (8.2.13) и (8.2.14) для радиусов колец выведены в предположении, что эта прослойка окружена одинаковыми средами, то есть пластинка и линза должны иметь одинаковые показатели преломления.

В качестве примера решения задач по этой теме, рассмотрим следующие задачи.

З а д а ч а  8. 2. 1 Свет от точечного монохроматического источника с длиной волным падает на экран "Э" (рис. 8.2), в котором имеются два маленьких отверстияи(опыт Юнга), расположенных на расстоянии3 м от экрана. Расстояние междуим (). Определить расстояние между максимумами интенсивности света смежных интерференционных полос (ширину светлой или темной полосы) на экране.

Дано: СИ м; м; 3 м.	Решение Рис. 8. 2
-?

Искомое расстояние между максимумами интенсивности смежных интерференционных полос на экране определяется как разность расстояний от центра картины (т. 0) до двух соседних темных полос с номерамии, то есть

Для нахождения ивоспользуемся условием образования минимума интенсивности света от 2-х когерентных источников для чего из рис. 8.2 найдем геометрическую разность хода 2-х лучей

где:

Вычитая из первого второе, получим

или

Откуда так как

Из условия минимума находим, что

(для ).

Следовательно, ширина темных и светлых полос одинакова, и равна

.

Подставляя числовые значения, рассчитаем

м.

Ответ: м.

З а д а ч а  8. 2. 2 Два когерентных источника, расстояние между которыми мм удалены от экрана нам. На длине экранасм располагаетсяполос. Чему равна длина волны монохроматического света, падающего на экран.

Дано: СИ м; м; м; .	Решение Так как ширина одной полосы (см. задачу 8.2.1) , то . Откуда
-?	м.

Ответ: м.

З а д а ч а  8. 2. 3 В опыте Юнга на пути одного из лучей монохроматического света с длиной волны м поместили перпендикулярно лучу тонкую стеклянную пластину с показателем преломления. При этом центральная светлая полоса сместилась в положение, первоначально занимаемое пятой светлой полосой. Какова толщина стеклянной пластины?

Дано: СИ м; ;	Решение Внесенная пластина изменяет оптическую разность хода световых лучей на величину Так, что теперь, условие возникновения максимума интенсивности света определяется выражением
-?

.

Откуда

м.

Ответ: м.

З а д а ч а  8. 2. 4 На мыльную пленку с падает под углом 60⁰ параллельный пучок белого света. Определить наименьшую толщину пленки, при которой в отраженном свете пленка имеет желтую окраску (м).

Дано: СИ м;; 600.	Решение В пучке белого света, упавшем на пленку, лучи с длиной волны , отразившись от верхней и нижней поверхностей пленки (см. рис. 8.1) в результате интерференции усилят друг друга, если выполнится условие (8.2.10):
-?

Отсюда толщина пленки равна

.

Минимальную толщину пленки будем иметь при .

м.

Ответ: м.

З а д а ч а  8. 2. 5 Для уменьшения потерь света при отражении от линзы фотоаппарата на поверхности объектива (линзы) с показателем преломления наносится тонкая прозрачная пленка с. При какой наименьшей ее толщине произойдет максимальное ослабление отраженного света, длина волны которого приходится на среднюю часть видимого спектра см. Считать, что лучи падают нормально к поверхности объектива.

Дано: СИ м; ; ; .	Решение Свет, падая на объектив, отражается как от передней, так и от задней поверхности тонкой пленки. Ход лучей для случая их наклонного падения (для ясности чертежа) показан на рис. 8.3, отраженные лучи 1 и 2 интерферируют. Так как , то оба луча 1 и 2 отражаются от оптически более плотной среды, а, следовательно, "теряют". Значит в выражении(8.2.1) теперь следует отбросить
-?

Рис. 8.3

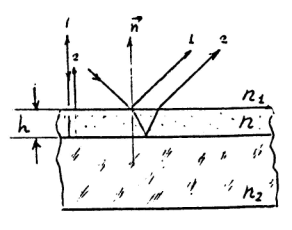
величину и тогда, с учетом того, что в задаче угол падения равен нулю, полная разность хода световых лучей составит,а условие минимума интенсивности света теперь будет таким

.

Откуда

Следовательно, искомая минимальная толщина пленки будет при условии то есть

м.

Это очень тонкая пленка, поэтому на практике изготовляют пленку толщиной , естественно увеличиваяв нечетное число раз.

Ответ: м.

З а д а ч а  8. 2. 6 На стеклянный клин с нормально к его грани подает параллельный пучок лучей монохроматического света с длиной волным. Числоинтерференционных полос приходящихся насм равно. Определить уголклина.

Дано: СИ м; ; м; .	Решение Лучи падая нормально к грани клина, отражаются как от верхних, так и от нижних границ. Лучи 1 и 2 являются когерентными. Поэтому на поверхности клина будут наблюдаться интерференционные полосы. Так как угол <<1, то отраженные лучи 1 и 2 (рис. 8.4) будут практически параллельны
-?

Рис. 8. 4

Темные полосы в отраженном свете видны на тех участках клина, для которых полная разность хода световых лучей кратна нечетному числу половин длин волн, то есть определяются тем же условием минимума интенсивности света, что и для плоскопараллельной пластины соответствующей толщине клина

(1)

Здесь учтено, что угол падения лучей равен нулю.

Из (1) следует, что

;. (2)

Искомый угол при основании клина найдем из прямоугольного треугольника, с учетом (2):

Так как угол <<1, то, и тогда

рад.

Для того, чтобы выразить в градусах, воспользуемся соотношением между радианом и градусом, получим

.

Используя соотношение между радианом и секундой:

рад,

получим .

Ответ: или.

З а д а ч а  8. 2. 7 Найти радиус кривизны плосковыпуклой линзы, лежащей на плоскопараллельной стеклянной пластине, освещаемая нормально падающим на неё монохроматическим светом длиной волны м. Радиус восьмого темного кольца Ньютона в отраженном свете равен 2 мм.

Дано: СИ м; ; м.	Решение Пучок параллельных лучей монохроматического света падает нормально к границе воздушного клина, заключенного между выпуклой стороной линзы и стеклянной пластиной. Падающий луч отражается частично от воздушного зазора (рис. 8.5) на кривизне линзы (луч 1), а частично
-?

о

Рис. 8.5

т стеклянной пластины (луч 2). Лучи 1, 2 когерентны. И в результате их положения на выпуклой стороне линзы наблюдается интерференция кольца. Темные кольца видны в тех местах, где полная разность хода этих лучейравна нечетному числу половин длин волн, то есть

(1)

где – толщина воздушной прослойки в том месте, где видно интерференционное кольцо;

– длина волны падающего света;

– номер темного кольца.

Величина в (1) – добавочная разность хода, возникающая при отражении луча 2 от оптически более плотной среды (пластина).

После упрощений, равенство (1) дает

. (2)

Из прямоугольного треугольника ОАВ (рис. 8.5) имеем

.

С учетом того, что , получаем

. (3)

Из (2) и (3) следует, что , откуда искомый радиус кривизны линзы равен

м.

Ответ: м.