ТЭЦ / Конспект лекций учебные пособия / архив / пер.пр

Тема занятия 19: Переходные процессы в RL –цепи.

19.1 Анализ переходного процесса при включении RL-цепи на постоянное напряжение.

Пусть цепь RL замкнута и содержит источник напряжения.

До коммутации, то есть в интервале цепь была разомкнута, источник отключен, ток в цепи равен нулю и напряжение на всех элементах равно нулю.

Уравнения для определения тока в переходном режиме следует составлять для состояния цепи после коммутации.

Для замкнутой цепи составим уравнения по второму закону Кирхгоффа: U_вх=U_R+U_L

Выразим: U_R=Ri U_вх=U, следовательно

U_L=L

- это дифференциальное уравнение первого порядка с правой частью.

Решением такого уравнения будет сумма двух решений – общего и частного.

- сумма вынужденной и свободной составляющих.

Чтобы определить вынужденную составляющую искомой переменной величины, следует все производные положить равными нулю и решить получившееся уравнение (использовать определение принужденной составляющей).

Если =0, следовательно , следовательно

- по окончании переходного процесса.

В цепи установится ток , так как индуктивное сопротивление при постоянном токе равно нулю, а сопротивление всей цепи равно активному.

Свободной составляющей называется составляющая тока изменяющаяся по такому закону, который обуславливается свойствами самой системы, а не какими-либо внешними воздействиями или причинами.

Чтобы определить законы свободной составляющей, следует в уравнении исключить внешнее воздействие, то есть положить напряжение равным нулю и решить получившиеся уравнения.

- это дифференциальное уравнение для нахождения свободной составляющей.

Решением данного уравнения будет: , где

А – постоянная интегрирования,

р- корень характеристического уравнения цепи. Чтобы его найти произведем замену:

и , следовательно характеристическое уравнение цепи

- свободная составляющая.

Величина - постоянная времени цепи RL.

,

Чтобы найти А, воспользуемся первым законом коммутации

i-(0)=i+(0)

Запишем значения тока в первый момент времени после коммутации:

, следовательно

Значение тока в последний момент перед коммутацией

, так как до коммутации ключ был разомкнут и в цепи ток не протекал.

Так как , то , следовательно

Значит:

- уравнение тока при включении RL цепи на постоянное напряжение.

Постоянной времени цепи называется время, за которое свободная составляющая тока или напряжения уменьшится в е раз, или это время, за которое ток достигает значения 0,63 от установившегося.

Если , то

Можно рассчитать, что ток достигает 99% установившегося значения через время равное 4,6, то есть .

19.2 Отключение RL цепи от источника постоянного напряжения.

В данном случае ток установившегося режима в катушке, не поддерживаемый ЭДС источника электрической энергии, начинает уменьшаться. При этом уменьшается магнитный поток катушки и в катушке индуцируется ЭДС самоиндукции, которая имеет одно направление с током, следовательно ток уменьшается не мгновенно, а за некоторое время переходного процесса.

Вынужденная составляющая равна нулю, так как через бесконечно большое время, тока в цепи не будет.

Для нахождения свободной составляющей, составляем уравнения по второму закону Кирхгоффа и приравниваем входное уравнение к нулю, так как его и нет в цепи.

, следовательно

, где - постоянная времени

Решение дифференциального уравнения:

Найдем параметр А, используется первый закон коммутации

Найдем параметр значение тока в первый момент после коммутации

(используется первый закон коммутации), следовательно

, следовательно

Тогда уравнение тока при отключении цепи:

Если t=, то .

Чем выше , тем медленнее идет переходной процесс. Постоянная времени определяется параметрами всех элементов, входящих в цепь.

П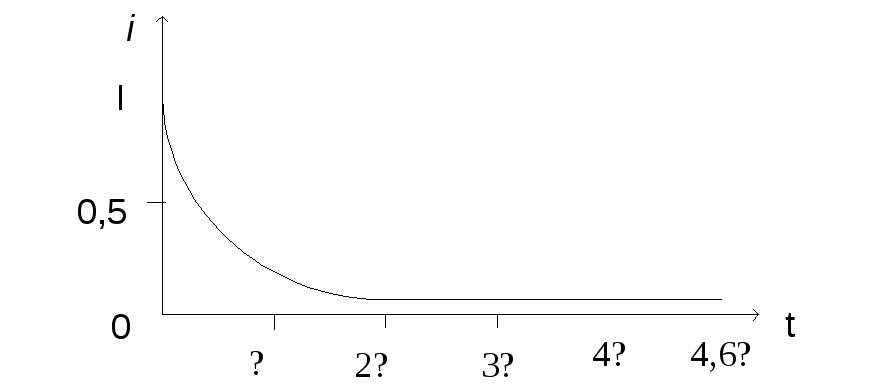остроим зависимость:

t=0 i=I

t= i=0,37I

t=2 i=0,137I

t=3 i=0,05I

t=4 i=0,018I

t=4,6 i=0,01I

Тема занятия: Переходные процессы в RC цепи.