30.1 Полосовые фильтры Баттерворта.

Данные фильтры пропускают токи определенной полосы частот.

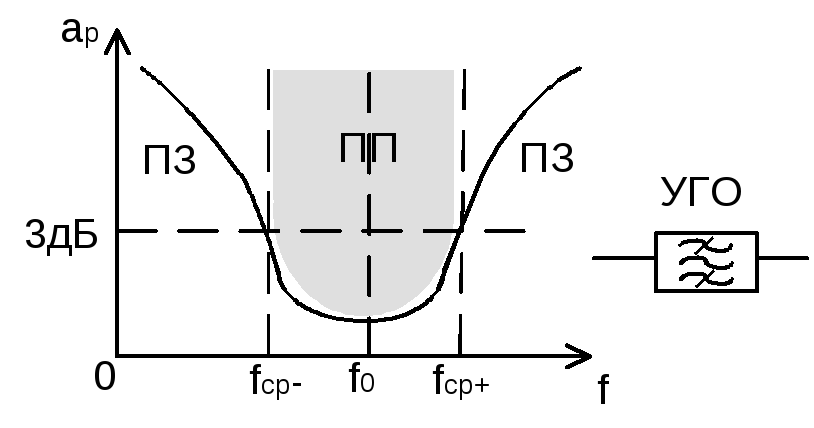
- центральная частота

,- граничные частоты.

На частотах меньших центральнойэквивалентная схема должна иметь вид ФВЧ Баттерворта. При частотах больших центральной – вид ФНЧ Баттерворта.

Чтобы получить характеристику полосового фильтра, надо взять ФНЧ и ФВЧ Баттерворта и совместить схемы.

Полосовой фильтр 4-го порядка.

Конденсаторы Сипрепятствуют прохождению токов низких частот. Эти токи замыкаются через катушки индуктивностии. Индуктивностиипрепятствуют прохождению токов высоких частот в нагрузку. Эти токи замыкаются черези. Все контуры настроены в резонанс на частоте.Сопротивление последовательных контуров (L,) мало, так как резонанс напряжений. Сопротивление параллельных контуров велико, так как резонанс токов. Поэтому токи полосы частот () с резонансной частотой последовательного колебательного контура оказывает малое сопротивление и ток этих частот легко проходит в нагрузку через последовательные контуры.

30.2 Расчет полосовых фильтров.

1. Находим центральную (резонансную) частоту

2 Рассчитаем коэффициент ширины полосы пропускания

;

3 Рассчитаем порядок фильтра

;

4 Рассчитаем постоянные преобразования

, мГн, нФ

5 Элементы рассчитываются отдельно для ФНЧ и ФВЧ

ФНЧ:

ФВЧ:

6 Рассчитываем .

.

Задача.

Рассчитать полосовой фильтр Баттерворта, если Ом, ПП=(16-25)кГц,дБ,

кГц. Найти.

30.3 Режекторные фильтры.

Не пропускают только полосу частот, остальные частоты пропускают.

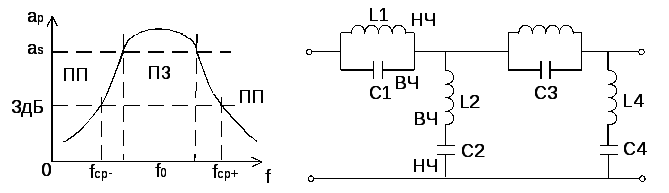
Катушки индуктивности ипропускают токи низких частот, а конденсаторыимешают им замкнуться через катушки индуктивностии. Конденсаторыипропускают токи высоких частот, аимешают им замкнуться черези, поэтому низкие и высокие частоты попадают в нагрузку.

Все контуры настроены на резонансную частоту , сопротивления параллельных колебательных контуров при резонансе велико, а последовательных мало, следовательно токи с резонансной частотойплохо проходят через параллельные контуры и замыкаются через последовательные, не попадая в нагрузку.

Тема занятия 31: Полиномиальные фильтры Чебышева.

Фильтры Чебышева отличаются от фильтров Баттерворта тем, что в полосе пропускания характеристика ослабления изменяется по колебательному закону. В полосе задерживания крутизна характеристики больше, чем у фильтров Баттерворта.

- максимально допустимое ослабление в полосе пропускания, дБ

Чем меньше , тем при том же порядке фильтра характеристика идет менее круто. Поэтому всегда выбирают фильтры с наибольшим допустимым, но не более 3 дБ.

Расчет рабочего затухания фильтра Чебышева:

- в полосе пропускания:

- в полосе задерживания:

То есть приведенные частоты рассчитываются так же как и у фильтров Баттерворта.

Схема фильтров Чебышева как и у фильтров Баттерворта, только элементы рассчитываются по специальным таблицам нормированных коэффициентов фильтров Чебышева. Они более громоздки, так как зависят от .

. Расчет порядка фильтра для фильтров Чебышева.

Задача. Рассчитать полосовой фильтр Чебышева, если полоса пропускания составляет (20-30) кГц, =2 дБ,=22 дБ,кГц,n=3.

Тема занятия 33: Фильтры Золотарева.