Угол сдвига фаз

Это разность начальных фаз двух переменных.

1 Та переменная, которая раньше достигает положительного максимума опережает по фазе, которая позже отстает по фазе - опережает по фазе,-отстает по фазе.

2 Если две переменные одновременно проходят максимум и ноль, то они совпадают по фазе.

Если угол сдвига фаз равен 180⁰, то переменные проходят в противофазе.

Временная и векторная диаграммы

Временная диаграмма- это зависимость переменной от времени t или от угла , если начальная фаза положительна, то она откладывается влево от начала координат, ели отрицательна- вправо.

Построим временную диаграмму для двух переменных

Временная диаграмма

Угол сдвига фаз равен

Любую синусоиду можно изобразить вектором. Длина, которого равна максимальному или действующему значению и расположен он под углом, равным начальной фазе к положительному направлению горизонтальной оси. Если начальная фаза положительна она откладывается вверх, если отрицательна - вниз.

Действующие значения переменных

Угол между векторами равен углу сдвига фаз между ними.

Тестовые задания:

Задание	Временные диаграммы				Варианты ответов
3.Укажите соответствие временных диаграмм и вариантов ответов.					а) U1 и U2 находятся в противофазе; б) U1 и U2 совпадают по фазе; в) U1 опережает по фазе U2; г) U2 опережает по фазе U1
Задание			Варианты ответов
1.Характеризует ли действующее значение сигнала его информационные свойства?			Да; Нет.
Задание		Математические выражения		Варианты ответов
2.Укажите соответствие математических выражений и вариантов ответов.		а) Ψn-Ψi б) 2πf в) г)		1) угловая частота; 2) циклическая частота; 3) угол сдвига фаз.

Комплексные числа в применении к электрическим цепям

-комплексное обозначение электрических величин. В некоторых учебниках ()

- алгебраическая форма комплексного числа

- показательная форма комплексного числа

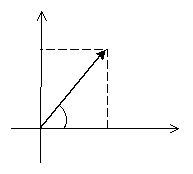
Изобразим комплексное число вектором ОМ.

Перевод комплексных чисел из одной формы в другую осуществляется следующим образом:

Дано число в алгебраической форме . Чтобы перевести его в показательную форму используем выраженияи. Если мнимая часть «b» отрицательна то угол «» также отрицательна.

Дано число в показательной форме Чтобы перевести его в алгебраическую форму используем выраженияи. Если уголотрицательный, то и мнимая часть будет отрицательной.

Пример перевода комплексных чисел.

1)

2)

3)

Чтобы записать ток в комплексной форме используют показательную форму записи комплексных чисел: модуль равен максимальному или действующему значению, а аргумент начальной фазе.

Например:

Запишем законы Ома и Кирхгофа в комплексной форме

Первый закон Кирхгофа:

Второй закон Кирхгофа:

Цепь с резистором при гармоническом воздействии

Приложим к резистору переменное напряжение . По закону Ома для мгновенных значений получим

Вывод: в цепи с резистором напряжение и ток совпадают по фазе

Временная диаграмма для

цепи с резистором.

Векторная диаграмма для цепи

с резистором.