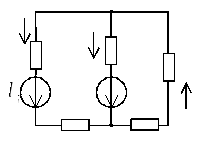
Метод наложения

Основан на принципе, согласно которому, ток в которой ветви может быть найден, как алгебраическая сумма токов от действия каждой ЕДС в отдельности

Порядок расчета

1. Поочередно оставляем в схеме по одному источнику

2. Внутренние сопротивления исключаемых источников остаются

3. Получаем расчет схемы для нахождения частичных токов. Эти токи обозначаем со « ′ » и рассчитываем по закону Ома

4. Находим действительные токи ветви, как алгебраическую сумму частичных токов. Действительный ток направлен в сторону большего действительного

Пусть при решении получилось

, ,. Тогда

Пример решения задачи:

Дано: E1=120 В Е2=128 В Ri1=2 Ом Ri2=1 Ом R1=10 Ом R2=19 Ом R3=40 Ом R4=3 Ом R5=20 Ом

R2-i2=19+1=20 Ом R3-5=40+20=60 Ом Ом Rвх=15+3+10=28 Ом А В А А R1-4=10+2+3=15 Ом R5-3=20+40=60 Ом Ом Rвх=12+19=31 Ом А В А А А А А

Получение синусоидального эдс

Синусоидальную ЭДС получают с помощью явления электромагнитной индукции. Рамку помещают в магнитное поле и равномерно вращают вокруг своей оси. Рамка пересекает магнитные линии и на ее концах наводится ЭДС электромагнитной индукции, которая изменяется по закону

ω- угол на который рамка поворачивается за 1с, называется угловой скоростью или угловой частотой.

[ω]=с^-1(рад/с)

, где f- циклическая частота, Гц

За время рамка поворачивается на угол ,тогда получим

Начальная фаза. Фаза

Угол, под которым рамка находится к положительному направлению к горизонтальной оси в нулевой момент времени называется начальной фазой. Начальная фаза может быть положительной и отрицательной.

Начальная фаза обозначается

Общее уравнение гармонических колебаний:

Начальная фаза определяет значение переменной в нулевой момент времени.

Фаза определяет значение переменной в любой момент времени.

Пример решения задачи.

Дано:

Найти:

(при (t)=0)

Решение:

В В

=314с^-1

f =50 Гц

с =20^о

Действующие значения переменного тока

Действующими значениями переменного тока называют такой постоянный ток, который за время равное периоду выделяет в сопротивление R, такое же количество тепла, что и переменный ток.

Действующее значение характеризует энергетические свойства сигнала. Мгновенное значение характеризует информационные свойства сигнала. Приборы показывают действующее значение.

Выведем формулу действующего значения переменного тока:

Энергия на постоянном токе = энергии на переменном токе.

Энергия на постоянном токе за период

Чтобы узнать энергию на переменном токе за периоднадо:

Рассчитать элементарную энергию за маленький промежуток времени , а затем все эти энергии сложить, то есть взять интеграл за период.

- действующее значение переменного тока.

Действующее значение еще называют среднеквадратичным значением.

Вывод: Действующее значение - это замена сигнала данной формы сигналом не изменяющемся во времени.

Выведем формулу, связывающую действующее и максимальное значение гармонического сигнала.

Пусть

=

Получается разность интегралов, где второй интеграл от гармонической функции

аналогично .

Формулы, которые связывают максимальное и действующее значения гармонического сигнала.