Параллельные цепи rl и rc при гармоническом воздействии

Если цепь параллельна, то векторную диаграмму начинают строить с вектора напряжений, т.к. напряжение участков при параллельном соединении одинаково.

Ток отстает от напряжения на угол(цепьRL), ток опережает напряжение на угол(цепьRC). Общий ток равен векторной сумме этих токов. Из диаграммы видно, что найти общий ток можно только специальным методом расчета. Этот метод называется метод составляющих токов. Построим подробную векторную диаграмму этой цепи. Строим вектор напряжений и токи и.

Разложим ток на две составляющие: активную, которая совпадает по фазе с напряжением и индуктивную, которая отстающее по фазе от напряжения на угол.

Эти составляющие определяем по формулам прямоугольного треугольника. ,, где;

Разложим ток на две составляющие: активную, которая совпадает по фазе с напряжением и индуктивную, которая опережает по фазе от напряжения на угол.

Эти составляющие определяем по формулам прямоугольного треугольника ,, где;

Складываем токи ина векторной диаграмме и получаем общий ток

Из треугольника АВС следует

Проводимости при гармоническом воздействии

Отношение активной составляющей тока к напряжению называется активной проводимостью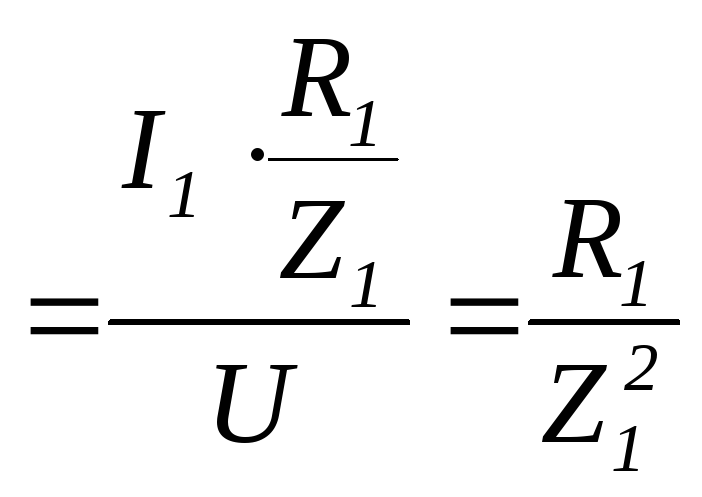,единица измерения всех проводимостей Сименс (См)

Аналогично

Отношение индуктивной или емкостной составляющей тока к напряжению называется реактивной проводимостью.

Отношение тока ветви или общего тока к напряжению называется полной проводимостью.

Отсюда - полное сопротивление

Разделим все стороны диаграммы токов на напряжение и получим диаграмму проводимости.

Из треугольника АВС получим

Если параллельно соединить по одному элементу, то формулы проводимости упрощаются:

проводимость обратна величине сопротивления. ,,Пример решения задачи

Дано:

В

Ом

Ом

Ом

Ом

Найти: методом составляющих токовОм

А

Ом

А

А А

А А

А

Чтобы рассчитать комплексное входное сопротивление при параллельном соединении используют формулу параллельного соединения резисторов. Вместо сопротивлений ставят их комплексные величины.

В числителе подставляем выражение в показательной форме, а в знаменатель в алгебраической.

Действительная часть комплексного входного сопротивления - это , мнимая-. Вывод: любую параллельную цепь можно заменить эквивалентной последовательной с параметрами,.

Тестовые задания:

Задание	Схема	Варианты ответов
1. Какое из приведенных математических выражений для расчета общего тока данной схемы является неверным?		а) ; б); в) ; г) .

Символический метод расчета электрических цепей

Комплексная мощность равна произведению комплексного напряжения на сопряженный комплекс тока, где сопряженный комплекс тока по модулю равен комплексу тока и противоположен по знаку аргумента .

Модуль комплексной мощности – это полная мощность цепи S

Действительная часть – это активная мощность цепи Р.

Мнимая часть - это реактивная мощность цепи Q.

Пример решения задачи.

Дано:

Найти:

Отсюда: полная мощность цепи S=В∙А, активная мощность цепиВт, реактивная мощность цепивар

Расчет электрических цепей символическим методом производится по формулам смешанного соединения резисторов, только вместо сопротивлений резисторов подставляется комплексное сопротивление участков.

Пример решения задачи.

Дано

В

Ом

Ом

Ом

Ом

Ом

Ом

Найти: , построить векторную диаграмму напряжений.

В∙А

Вт

вар