12.1 Входные ачх и фчх параллельного контура.

входная ФЧХ параллельного колебательного контура

Построим график:

ξ=∞ Z=0

Вывод: параллельный колебательный контур имеет наибольшее сопротивление на резонансной частоте, по мере увеличения расстройки сопротивление уменьшается.

φ=arctg(+X/R)=arctg(-ξ) - входная ФЧХ параллельного колебательного контура.

Построим график:

ξ→ -∞ φ → 90°

ξ = 1 φ = -45°

ξ = -1 φ = 45°

Вывод: ФЧХ параллельного колебательного контура представляет собой зеркальное отображение ФЧХ последовательного контура. На частотах меньших частоты собственных колебаний контур носит активно-индуктивный характер, на резонансной частоте – чисто активный, на частотах больших частоты собственных колебаний – активно –емкостной характер.

12.2 Подключение параллельного колебательного контура

к источникам тока и напряжения.

Для параллельного колебательного контура:

- общий ток цепи при резонансе.

- ток в ветвях цепи.

Найдем соотношение:

, где Q – добротность контура, показывает, во сколько раз ток в разветвленной ветви больше тока в неразветвленной части цепи.

В реальных устройствах выходное напряжение снимают с конденсатора. Если параллельный колебательный контур подключен к источнику напряжения с малым внутренним сопротивлением, то напряжение на входе равно напряжению на выходе и K=1, то есть колебательный контур не обладает избирательностью по напряжению. Ток в неразветвленной части цепи не остается постоянным.

Чтобы параллельный контур обладал избирательностью по напряжению , его необходимо подключить к источнику тока, то есть последовательно с ЭДС включить большое внутреннее сопротивление:

, тогда I=U/(Ri+Zвх)= сonst

Схема с источником напряжения преобразуется в схему с источником тока.

Наличие резистора изменит добротность цепи.

Uвых=IUвх, следовательно так как I=const, то выходное напряжение изменяется по закону входного сопротивления контура, то есть контур обладает избирательностью

Построим графики зависимостей Uвых(f) и I(f) для обеих схем.

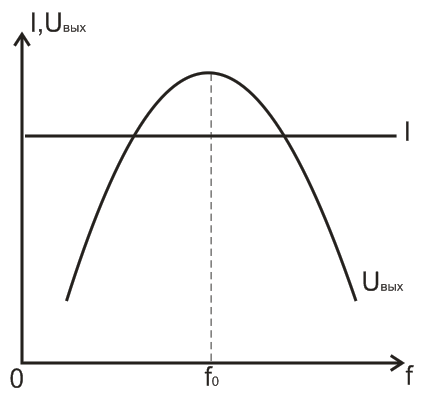
Для схемы с источником напряжения. Для схемы с источником тока.

Вывод: Колебательный контур обладает избирательностью по напряжению, если контур подключен к источнику тока.

Так как для схемы с источником тока при вводе сопротивления Ri изменяется добротность цепи, то используется понятие эквивалентной добротности.

Q=ρ/R Qэ=Q/(1+Zвх/Ri)

В реальных устройствах

и .

Эквивалентная обобщенная расстройка:

.

12.3 Передаточные ачх параллельного колебательного контура.

Модуль передаточной функции:

K = Uвых / Uвх = IZвх/ Uвх = Qρ / Ri √1+ξэ² - передаточная АЧХ параллельного колебательного контура

- коэффициент передачи при резонансе( ξэ=0) → max.

Найдем отношение

k/ko=1/√1+ξэ² -передаточные АЧХ параллельного колебательного контура в относительных единицах

Построим график:

- полоса пропускания абсолютное значение

- полоса пропускания относительное значение

Вывод: избирательность по напряжению получается , когда k<1, так как входное сопротивление значительно меньше внутреннего.

Задача: На рисунке дана схема. Найти емкость, добротность входное сопротивление, эквивалентную добротность, напряжение входа и ρ, если

Fо=60Мгц

L=0,35 мкГн

R=5 Ом

E=10 мкВ

Ri=3 кОм.

Решение: