9.3 Избирательность и полоса пропускания последовательного контура.

Избирательность – способность контура усиливать напряжения на различных частотах в неодинаковое число раз.

Контур как бы «выбирает» из спектра напряжения на тех частотах, которые близки к резонансной.

Коэффициент передачи по напряжению в последовательном колебательном контуре зависит от частоты, поэтому при подведении на вход контура спектра частот с одинаковыми амплитудами на выходе получается спектр тех же частот, но с различными амплитудами, так как напряжение выхода равно произведению коэффициента передачи и входного напряжения.

Самый большой сигнал получается на резонансной частоте, так как коэффициент передачи наибольший.

Полоса пропускания – диапазон частот, в пределах которых коэффициент передачи уменьшается не более чем в раз по сравнению с максимальным значением.

Граничная частота – частота, на которой коэффициент передачи составляет 0,707 от коэффициента передачи на рехонансной частоте.

Различают:

1. Абсолютное значение полосы пропускания

Π=2∆f=fo∕Q [Гц]

2. Относительное значение полосы пропускания:

Чем выше добротность контура, тем уже полоса пропускания контура.

fгр. ниж = fo-fo∕2Q [Гц]

fгр. вер = fo+fo∕2Q [Гц]

Определим кривую тока:

и построим ее

4. Электронный аналог

Пассивный колебательный контур содержит катушку, которую в микроэлектронном исполнении изготовить сложно, поэтому колебательной контур заменяют активной цепью, выполненной с помощью операционного усилителя, который имеет такую же передаточную характеристику АЧХ в виде резонансной кривой.

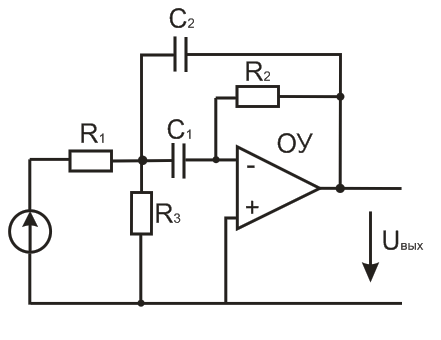
Преимущество данной системы:

-настройка колебательного контура осуществляется путем изменения сопротивления на резисторах R₂ и R₃, что конструктивно проще выполнить.

Недостаток:

-при изменении R₂ и R₃ меняется добротность и коэффициент передачи контура.

Задача: Рассчитать индуктивность, емкость, сопротивление, напряжения входное и емкостное, полосу пропускания, частоту при резонансе в последовательном колебательном контуре, если добротность 125, ρ=500 Ом и ί=0,1 sin 94,2 * 10‘t.

Решение:

Тестовые задания:

Тема занятия 11: Резонанс токов

Пассивный параллельный колебательный контур – цепь, в которой элементы L и C подключены параллельно источнику энергии.

Резонанс токов – явление, при котором ток в неразветвленной части минимален. При этом он может быть значительно меньше токов в разветвленных ветвях и совпадать по фазе с входным напряжением.

Условия возникновения резонанса:

1. Параллельное соединение элементов L и C

2. Равенство реактивных проводимостей

3. Минимальная величина активного сопротивления, обеспечивающего возникновение свободных колебаний в контуре.

Общая проводимость цепи:

ток и напряжение совпадают по фазе.

- реактивные проводимости ветвей.

Частота тока генератора, при котором возникает резонанс токов, определяется из условия равенства реактивных проводимостей параллельных ветвей.

Следовательно, резонансная частота последовательного колебательного контура равна резонансной частоте параллельного колебательного контура.

Резонанс токов наступает тогда, когда частота питающего генератора равна частоте собственных колебаний контура.

Получить резонанс в параллельном контуре можно теми же способами, что и в последовательном колебательном контуре, то есть изменением частоты питающей сети, емкости или индуктивности.

Так как в момент резонанса ток минимален, то

,

где Q=ρ∕R – добротность контура.

Рассмотрим значения тока в момент резонанса:

– минимальный общий ток в цепи.

, то есть токи ветвей в момент резонанса равны.

На практике

Построим векторную диаграмму токов.

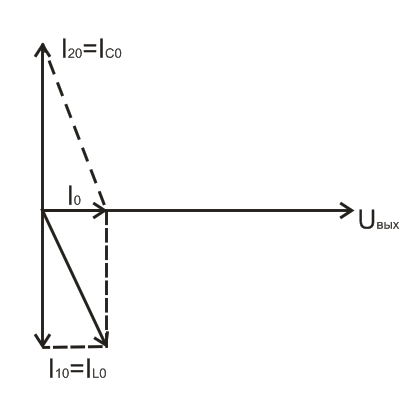Общий ток по фазе совпадает по фазе с напряжением и он меньше токов ветвей цепи.

В идеальном колебательном контуре суммарный ток параллельных ветвей при резонансе равен нулю, то есть в контуре протекают токи I₁ и I₂ без учета генератора. Энергия от генератора конденсатора не тратится, и в контуре возникают незатухающие колебания.

В реальном колебательном контуре имеется обмен энергией между электрическим полем конденсатора и магнитным полем катушки индуктивности в равных количествах. От генератора поступает столько энергии в контур, сколько тратится безвозвратно на его активных сопротивлениях.

S=Pcosφ=Po=IoU

cosφ=1 Q=0.

График зависимости токов в реальном контуре:

Задача: Определить входное сопротивление для последовательного и параллельного колебательных контуров, если индуктивность составляет 400 мкГн, емкость 1600 пФ, сопротивление 30 Ом.

Решение:

Тема занятия 12: Избирательные свойства

параллельного колебательного контура.